简单的信号表示与matlab（含抽样频率

• 代码来自北邮MOOC《信号与系统》，仅做学习总结

离散信号的表示

• 单位样值信号

n = [-5:5];
x = [0 0 0 0 0 1 0 0 0 0 0];
% 画序列图，列宽为2
stem(n,x,'linewidth',2);
xlabel('n');
ylabel('x(n)');

• 有限长序列

x = [1 2 4 2 3];
n = -2:2;
stem(n,x);
xlabel('n');
ylabel('x(n)');

• 单边指数序列，text标注，power形成指数

n = 0:10;
x1 = power(0.8,n)
stem(n,x1,'linewidth',2)
xlabel('n');
ylabel('a^n');
axis([n(1) n(end) -1.5 1.5]);
text(7,1,2,'a = 0.8');

• 正弦序列
  • $x(n)=cos(n{\omega }_0+\theta )$
  • w0数字角频率

n = 0:31;
w0 = pi/8;
x = sin(w0*n);
stem(n,x,'linewidth',2);
xlabel('n');
ylabel('x(n)');
axis([0 max(n) -1.1 1.1]);

• 矩形脉冲序列 window 矩形窗
  • $R_N(n)=u(n)-u(n-N)$

N = 11;
n = (0:N-1)';
w = window(@rectwin,N);
stem(n,w,'linewidth',2);
xlabel('n');
ylabel('R_N(n)');
ylim([0 1.5])

连续信号

• 复指数信号
  • $x(t)=e^{(\alpha +j\omega )t}$
  • 转为实数信号画图

clear all;close all;
t0 = 0;
tf = 5;
dt = 0.01;
t = [t0:dt:tf];
alpha = -0.5;
w = 10;
x = exp((alpha+j*w)*t);
subplot(2,2,1);
plot(t,real(x),'linewidth',2)
xlim([t(1) t(end)])
grid on;
xlabel('t');ylabel('real part');
suplot(222);
plot(t,img(x),'linewidth',2)
suplot(223);
plot(t,abs(x),'linewidth',2)
suplot(224);
plot(t,angle(x),'linewidth',2)

• 相位解卷绕
  • 相位图去掉了 $2\pi$ 的整倍数，图形分布在 $(-\pi ,\pi )$ ，称为卷绕
  • unwrap: 解卷绕

x_ang = angle(x);
x_ang_unwrap = unwrap(x_ang)
plot(t,x_ang_unwrap);
grid on;
xlabel('t');ylabel('angle');

抽样信号

• NaN 不是一个数， 使用sinc
  • $Sa(t)=\frac{sin(t)}{t}$
  • $Sa(t)=sinc\{\frac{t}{\pi }\}$

t = linspace(-10,10,101);
x = sin(t)./t;
plot(t,x);
% sin(0)./0 Warning:Divided by a zero ans = NaN

• sinc(t/pi) 与 sinc(t)

t = linspace(-10,10,501);
x = sinc(t/pi);
subplot(211);
plot(t,x);grid on;
xlabel('t');ylabel('Sa(t)'); % 过零点pi的整倍数
y = sinc(t);
subplot(211);
plot(t,y);grid on;
xlabel('t');ylabel('sinc(t)');%  过零点整数

钢琴

• 钢琴键盘中央 “C” 对应的频率约为262Hz，请产生1秒钟的此频率信号，抽样频率8192Hz
• 正弦波模拟钢琴震动

$$\begin{gathered} x(t)=sin(2\pi f_{0}t) \\ x(nT)=x(t){|}_{t=nT} \\ =sin(2\pi f_{0}nT)=sin(2\pi f_{0}n\frac{1}{f_s})=sin({\omega }_{0}n) \end{gathered}$$

f0 = 262;
fs = 8192;
omega0 = 2*pi*f0/fs; % 1s数据
n = 0:fs-1;
x = sin(n*omega0);
sound(x,fs);
audiowrite('dou.wav',x,fs);

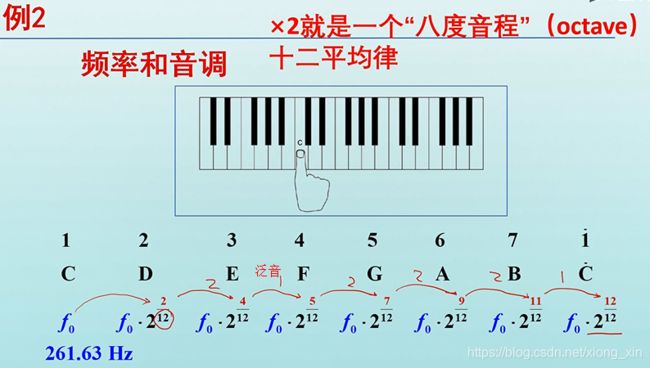
频率与音调

• 人耳对声波的频率是指数敏感的，某一组声音如果频率严格地按照 $2^n$ 的规律排列，它们听起来才是一个“等差音高序列”
• X2就是一个“八度音程“ (octave) 十二平均律

fs = 8192;
n = 0:fs/2-1
f1 = 262;
f2 = f1*power(2,2/12);
f3 = f1*power(2,4/12);
f4 = f1*power(2,5/12);
f5 = f1*power(2,7/12);
f6 = f1*power(2,9/12);
f7 = f1*power(2,11/12);
fh1 = f1*power(2,11/12);

x1 = sin(n*2*pi*f1/fs);
x2 = sin(n*2*pi*f2/fs);
x3 = sin(n*2*pi*f3/fs);
x4 = sin(n*2*pi*f4/fs);
x5 = sin(n*2*pi*f5/fs);
x6 = sin(n*2*pi*f6/fs);
x7 = sin(n*2*pi*f7/fs);
xh1 = sin(n*2*pi*fh1/fs);

x = [x1 x2 x3 x3 x5 x6 x7 xh1];
sound(x,fs);
% 简单的曲子
y = [x3 x3 x4 x5 x5 x4 x3];
sound(y,fs);

忙音信号

• “嘟、嘟、嘟……”的短促音(450Hz，响0.35s，断0.35s)

fs = 8000; % fs:抽样频率
Ts = 1/fs; % Ts:抽样间隔
f = 450;% 电话信号音的频率
T = 0.35;% 忙音通和断的时长
t = 0:Ts:T;% 抽样间隔
%电话信号音
x1 = sin(t*2*pi*f);
x2 = zeros(size(x1));
x = [x1 x2];
y = [x x x x];
sound(y,fs);

符号数学工具箱

• $x(t)=sin(2\pi t/T)$
• subs 用于替换 T =5

syms t T;
w = 2*pi/T;
x = sin(w*t);
x1 = subs(x,'T',5);
ezplot(x1,[0 10]);

• 计算信号 $x(t)=Asin(2\pi t/T)$ 的平均值和平均功率
• int 积分从0到T

clear all
syms t T A;
w = 2*pi/T;
x = A*sin(w*t);
M = int(x,0,T)/T % 平均值
P = int(x^2,0,T)/T % 平均功率

• 对信号先分别创建再相乘，对于T = 4,用ezplot画出t在[0,4]内的信号，x(t)的基波周期用T表示

$$x(t)=cos(2\pi t/T)sin(2\pi t/T)$$

clear all
syms t T;
A = cos(2*pi*t/T);
B = sin(2*pi*t/T);
x = A*B;
x1 = subs(x,'T',4);
ezplot(x1,[0,4]);

• 有一线性时不变系统，当激励 $x_1(t)=u(t)$ 时，零状态响应为 $y_1(t)=e^{-2t}cos(3t)u(t)$ ，试求当激励 $x_2(t)=\delta (t)$ 时，零状态响应 $y_2(t)$ 的表达式
  • $y_2(t)=\frac{d{y}_1(t)}{dt}$
  • u(t) 用 heaviside 表示
  • simplify 表示化简

clear all;
syms t;
y1 = exp(-2*t)*cos(3*t)*heaviside(t);
y2 = diff(y1);
y3 = simplify(y2);

• 升余弦脉冲信号，画出波形图，并求其能量

$$x(t)=\frac{1}{2}[1+cos(\omega t)][u(t+\pi /\omega )-u(t-\pi /\omega )]$$

clear all;
syms t w;
x = (1+cos(w*t))/2;
E = int(x^2,t,-pi/w,pi/w);
x1 = subs(x,'w',pi);
ezplot(x1,[-1,1]);