【量化笔记】Markowitz均值-方差模型

Markowitz均值-方差模型是一种确定在N种资产上投资比例的模型

假定现在投资人初始财富$W_0$，在N种资产上的投资比重分别为$w_1,w_2,w_3,...,w_N$,未来期望收益率为$R_p$

投资者的目标是收益最大化的同时，使风险最小化

所以投资过程可以抽象为：
$$\begin{gathered} ma{x}_{w_i}\mathbb{E}[U(R_p)]=\mathbb{E}[U({\sum }_{i=1}^N{w}_i{R}_i)] \\ s.t.{\sum }_{i=1}N{w}_i=1 \end{gathered}$$（收益最大化）

$$\begin{gathered} mi{n}_{w_i}{\sigma }^2(R_p)={\sum }_{i=1}^N{w}_i^2{\sigma }^2(R_i)+{\sum }_{i<>j}{w}_i{w}_j\sigma (R_i,R_j) \\ s.t{R}_p={\sum }_{i=1}^N{w}_i\mathbb{E}(R_i) \\ {\sum }_{i=1}^N{w}_i=1 \end{gathered}$$(风险最小化)

假设$R_1,R_2,...,R_N$均服从正态分布，进一步假设$U(.)$是常见的凹函数。

跳过一系列解方程的过程，这是一个二次规划问题，最后解的形式为：
$w^{\ast }=a+b{R}_p$
其中$$\begin{gathered} a=\frac{\zeta {\Sigma }^{-1}e-\alpha {\Sigma }^{-1}\overline{R}}{\zeta \delta -{\alpha }^2} \\ b=\frac{\delta {\Sigma }^{-1}\overline{R}-\alpha {\Sigma }^{-1}e}{\zeta \delta -{\alpha }^2} \end{gathered}$$
其中
$$\begin{gathered} \alpha ={\overline{R}}^{\prime }{\Sigma }^{-1}e \\ \zeta ={\overline{R}}^{\prime }{\Sigma }^{-1}\overline{R} \\ \delta =e^{\prime }{\Sigma }^{-1}e \end{gathered}$$
只考虑风险资产的效率前缘：

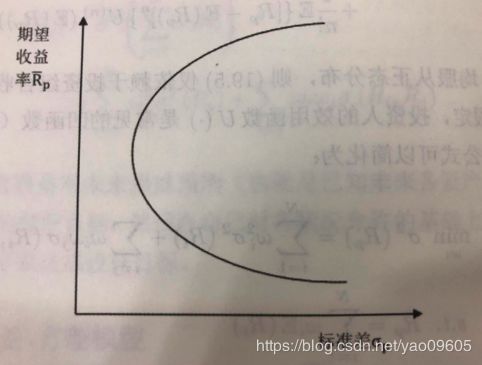
下面考虑存在无风险投资的情况，比如银行存款，假设无风险投资的收益率为$R_f$

那么我们的投资模型可以重新抽象为：
$$\begin{gathered} mi{n}_{w_i}{\sigma }^2(R_p)={\sum }_{i=1}^N{w}_i^2{\sigma }^2(R_i)+{\sum }_{i<>j}{w}_i{w}_j\sigma (R_i,R_j) \\ s.t.{\overline{R}}_p=R_f+{\sum }_{i=1}N{w}_i[\mathbb{E}(R_i)-R_f] \end{gathered}$$

求解结果是：
$w^{\ast }=\frac{{\overline{R}}_p-R_f}{\zeta -2\alpha R_f+\delta R_f^2}{\Sigma }^{-}1(\overline{R}-R_{f}e)$

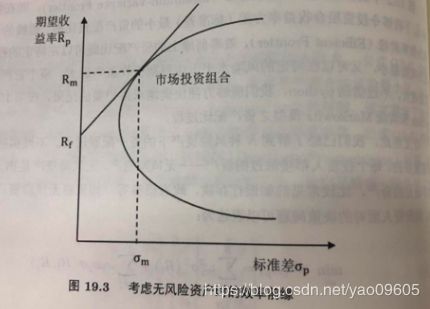
图中直线的表示了风险和收益的关系，风险越高收益越高，这是符合直觉的。
表达式为：
$\mathbb{E}(R_p)=R_f+\frac{\mathbb{E}(R_m)-R_f}{{\sigma }_m}{\sigma }_p$

如此可以得到CAPM模型的结论：对于任何资产组合q，其收益率$R_q$满足
$\mathbb{E}(R_q)=R_f+{\beta }_{qm}[\mathbb{E}(R_m)-R_f]$
其中${\beta }_{qm}=\frac{\sigma (R_q,R_m)}{{\sigma }^2(R_m)}$
投资组合也可以是单一资产：
$\mathbb{E}(R_i)=R_f+{\beta }_{im}[\mathbb{E}(R_m)-R_f]$
其中${\beta }_{im}=\frac{\sigma (R_i,R_m)}{{\sigma }^2(R_m)}$