RBM的理解
前言
对RBM(Restricted Boltzmann Machine)的理解进行简单的总结。
主要涉及RBM的图结构,为什么场能E(v,h)要如此定义,优化的思路到底是怎么来的,MRF与MC在优化时起到怎么样的作用,CD的意义,RBM的实现。
RBM
RBM是个两层的网络,层间连接,而层内无连接(restricted的由来)。可以理解为是个表示了概率分布的参数模型(概率图模型),也可以认为是个神经网络。基本结构如下:
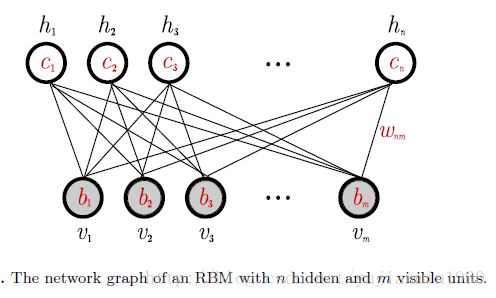
RBM的目标
BM是层内也连接的RBM,最终状态是能够学习得到训练集的分布。RBM对层内的限制是为了减少计算困难,并提供条件独立的基本结构。
图、MRF、Gibbs分布、RBM
为了能够简洁地描述RBM所表示的分布,对节点状态之间的依赖关系作以下假设,节点状态与其他节点状态条件独立与该节点的近邻节点状态(MRF markov random field)。然后,可以证明RBM结构下的MRF的联合分布可分解为Gibbs分布。简直好的不要不要的~
1)RBM的图结构
如上图, G=(V,E) ,对每个节点 v ,节点状态 Xv 都可以表示为随机变量。
2)图G为MRF 与 图联合分布为Gibbs分布 的关系–>等价:
图的随机变量条件独立 与 图的联合分布可分解 是等价的,MRF的联合分布可以被分解[32, 29](Hammersley-Clifford Theorem)。(分解的好处,就是方便表示和计算啊)
无向图G为MFR:

无向图G联合分布可分解:

上述两个定义是等价的(有兴趣的童鞋一定要看看等价关系的证明 [2],很妙~),因此,对于RBM满足MRF条件,则其联合概率分布可以分解为 p(X)=1Z∏c∈CGϕc(Xc) 。
3)RBM的联合分布
通过definiton2可以看到,对定义在图G的极大团集上的正值函数 ϕ ,都可以表示成Gibbs分布的形式。那么在RBM中,我们指定一个函数定义 ϕ(xi,j)=p(vi,vj)=ewi,jhivj+cihi+bjvj ,其中 {i,j}=c,且c∈{maxmial−clique}G ,该函数定义在所有极大团上且 ϕ>0 ,进一步得到RBM的联合分布
化简为向量形式:
其中Z=∑v,he−E(v,h),E(v,h)=−hwv−ch−bv
OK,现在弄明白 RBM的联合概率分布是怎么来的了~
补充:也可以从另外的方向化简,结果一样,如下。
p(x)=1Z∏ψ(xc)=1Ze∑lnψ(xc)=p(v,h)=1Ze−E(v,h)=1ZehWv+bv+hc
最大似然与梯度下降
已知分布形式,剩下的就是根据输入数据调参了,最为常见的就是最大似然方法了。
但是,我们对RBM的边缘分布 p(v) 更感兴趣, p(v)=∑hp(v,h)=1Z∑he−E(v,h) 。下面对其采用最大似然的思路尝试优化。
最大化 L(θ|Data) ,从而求得最优参数。
单个样本的的似然函数如下:
其梯度如下:
难点:期望难求,需要遍历所有可能。前半部分是在概率 p(h|v) 下的随机变量 ∂E(v,h)∂θ 期望取负,后半部分是在概率 p(v,h) 下的随机变量 ∂E(v,h)∂θ 的期望。
进一步分开参数 θ={wij,bj,ci} , E(v,h)=−hwv−ch−bv 化简,都存在类似计算problem。
⎧⎩⎨⎪⎪⎪⎪⎪⎪⎪⎪∂L(θ|v)∂w=∑hp(h|v)hv−∑v,hp(v,h)hv∂L(θ|v)∂b=∑hp(h|v)v−∑v,hp(v,h)v∂L(θ|v)∂c=∑hp(h|v)h−∑v,hp(v,h)h => ⎧⎩⎨⎪⎪⎪⎪⎪⎪⎪⎪∂L(θ|v)∂w=E[hv]|p(h|v)−E[hv]|p(v,h)∂L(θ|v)∂b=E[v]|p(h|v)−E[v]|p(v,h)∂L(θ|v)∂c=E[h]|p(h|v)−E[h]|p(v,h)
我想,大神们应该是从这里受到启发,开始搞梯度的估计的思路的~RBM满足MRF为自身MC的gibbs采样提供了期望采样的可能。
有没有发现,单样本下涉及了期望,如果对多个样本,岂不是可以用采样集的均值作为样本期望了,样本均值估计总体期望,是常见思路。RBM的开创大神们将这条路走到底,进一步将样本集部分加进来~如下~
⎧⎩⎨⎪⎪⎪⎪⎪⎪⎪⎪1l∑v∈D∂L(θ|v)∂w=1l∑v∈D[E[hv]|p(h|v)−E[hv]|p(v,h)]1l∑v∈D∂L(θ|v)∂b=1l∑v∈D[E[v]|p(h|v)−E[v]|pv,h]1l∑v∈D∂L(θ|v)∂c=1l∑v∈D[E[h]|p(h|v)−E[h]|p(v,h)]
==>⎧⎩⎨⎪⎪⎪⎪ΔwL(θ|D)=⟨hv⟩p(h|v)p(v)−⟨hv⟩p(v,h)ΔbL(θ|D)=⟨v⟩p(v)−⟨v⟩p(v,h)ΔcL(θ|D)=⟨h⟩p(h|v)p(v)−⟨h⟩p(v,h)
其中 p(v) 表示样本分布,于是得到各个参数的梯度: ⎧⎩⎨⎪⎪⎪⎪ΔwL(θ|D)=⟨hv⟩data−⟨hv⟩modelΔbL(θ|D)=⟨v⟩data−⟨v⟩modelΔcL(θ|D)=⟨h⟩data−⟨h⟩model 。其中, ⟨⋅⟩ 表示均值。
剩下的问题就是解决在参数 θ 下模型的采样均值问题。
Markov Chain 与 Gibbs Sampling
前面有提到,RBM满足MRF,即其非近邻节点状态互相条件独立(Markov property)定义1刚好对RBM结构来说,可以将节点状态的更新过程,转化为MC的更新过程,又感慨世界多奇妙了~而MC的稳态不依赖于初始值,只与系统本身有关,可以在稳态的基础上采样得到 p(v,h|θ) 下的稳定系统样本均值。完美地解决了模型稳态下样本均值的计算(期望地估计)。
Markov Chain
马尔科夫链是离散时间随机过程,系统下一状态只依赖于当前状态 p(k)ij=p(x(k+1)=j|x(k)=i) 。Markov property: 当前节点状态只依赖于近邻;下一状态只依赖于当前。是不是很相像,两者本质是一样的,这是将MC与基于RBM采样联系到一起的关键。
平稳分布:如果分布 π 满足, πT=πTP ,其中 P=(pij)称为状态转移矩阵 。
马尔科夫链稳定的定义:
⎧⎩⎨⎪⎪⎪⎪初始概率分布u(0)=u(0)(i)|i∈状态空间 时间k后,概率分布u(k)=u(k)(i)|i∈状态空间=u(0)Pk 当uk=π,其中π=πP,转移矩阵P为常数矩阵。 =>MC达到稳态分布π
马尔科夫链稳定的充分条件: π(i)pij=π(j)pji
马尔科夫链稳定的充分条件2:一个不可约且非周期,并且具有有限状态的马尔科夫链,一定能够收敛到稳态。非常重要
不可约:在状态空间有限的情况下,一个状态可以经过有限次数转移到另外任意状态。
非周期:状态不周期复现。
收敛定理[3]: 假设一个状态有限且不可约非周期的MC,的稳态分布为 π ,转移矩阵 P ,对任意的起始概率 u ,都会有
其中, dV(α,β)=12|α−β|=12∑x∈Ω|α(x)−β(x)| 描述两个分布 α 和 β 在有限状态空间 Ω 的distance of variation。
马尔科夫链的收敛定理,为我们对RBM下的似然函数的梯度里的期望计算提供了理论依据。随意初始RBM起始状态,按照gibbs采样足够次数后,必然得到RBM联合分布下的样本。
Gibbs Sampling
RBM在Markov property下的不同时刻的状态变化可以满足状态有限且不可约非周期的MC。证明见[1]的3.2节。
因此,对RBM可以在输入 v 的情况下,多次采样。
采样方法化简后如下(这里的采样方法由于RBM的节点间条件独立得以非常简单):
1. sample h given v
2. sample v given h
以此循环。将最后的 v 作为第k次采样的系统v节点状态,可以认为是系统在当前参数下的稳态v节点状态样本。
OK,到这里,貌似就将梯度的估计搞定了,采样计算均值。依稀觉得哪里不对劲,是的,采样需要进行足够多次才能得到稳态分布的样本,这是个problem。那我如果采样有限的次数,是不是也OK呢。下面就给出肯定答案,采样一步就足够了。
Constractive Divergence
两个分布的不对称性,可以用 Kullback Leibler divergence 来衡量,当分布一致时,其值为0.
前面有博客 最大似然与交叉熵的一致性讲过,在样本类别唯一时,最大化最大似然与最小化交叉熵是等价的,也等价于 最小化KL-divergence。
根据收敛定理,gibb采样分布 pk 比初始数据分布 p0 更接近稳态分布 p∞ 。接下来的思路有两个,一个显得很朴素便于理解,一个绕个大圈子显得逼格很高的样子。
超朴素的思路一:既然 pk 更为靠近 p∞ ,那么采样有限的几步也是可以提供梯度的方向的,虽然并不精准。但是我们只需要是朝着大概正确的方向前进即可,大不了多迭代几次嘛。这个想法,跟凸优化里面的次梯度下降法有异曲同工之妙,只要朝着梯度下降的方向就好。OK,那么选择 k=1 也可以估计梯度了,完毕。
高逼格的思路二:最小化 KL(p0||p∞) 作用 等效于 最小化距离的距离: CD(p0|pk)=KL(p0||p∞)−KL(pk||p∞) 。
对CD求导: −∂CD(p0|pk)∂θ=⟨∂lnp(v|θ)∂θ⟩p0−⟨∂p(vk|θ)∂θ⟩pk+∂KL(pk||p∞)∂pk⋅∂pk∂θ
估计上式: −∂CD(p0|pk)∂θ≈⟨∂lnp(v|θ)∂θ⟩p0−⟨∂p(vk|θ)∂θ⟩pk
再次估计: −∂CD(p0|pk)∂θ≈−∂CD(p0|p1)∂θ≈⟨∂lnp(v|θ)∂θ⟩p0−⟨∂p(v1|θ)∂θ⟩p1
于是得到: Δθ|CD(p0|p∞)∝⟨∂lnp(v|θ)∂θ⟩p0−⟨∂p(v1|θ)∂θ⟩p1
哈哈,得到CD下的梯度估计了(有专门就CD估计的bias的分析文章[5])。这个时候,是不是看着跟最大似然的梯度很相近,当然一致了。这里在对最大似然与交叉熵和KL散度的一致性说明下:
最大似然的优化函数: lnL(v|θ)=ln∏p(v|θ)T[y]
交叉熵的优化函数: CE(p,y)=∑T[y]⋅lnp(v|θ) 化积为和。
KL-散度的优化函数: KL(y||p)=∑ylny−∑ylnp(v|θ) ,交叉熵的部分。
CD-的优化函数: CD(y|y1)=−∑ylnp(v|θ)+∑ylnp(v1|θ)
优化函数,在连续性和一致性上都没有本质变化,那么梯度也必然是共通的(抛开正负方向)。
思考:
CD这块看着很无用的样子,但是给出了梯度估计的理论支撑。再往深处想一下,会发现Grdient Boost的想法也隐含其中,GB借助函数空间的导数给出了下一个函数构建时的方向,这里数据-GibbsSampling给出了模型与预期之间的差距,也相当于给出了理想更新模型状态的方向。不同的是,前者刚好提供了理想与现实间的差距,后者则是刚好提供了梯度的估计。
估计,则是在大体方向正确的前提下的简化。
补充知识
1) 随机变量
2) 图的相关概念
主要是图结构定义,图markov-property,maxmial-clique,maxmium-clique
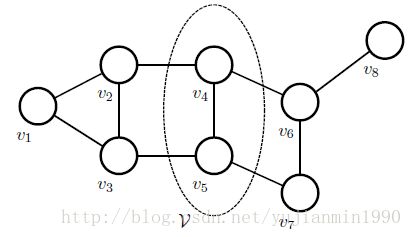
图描述: G=(V,E) ,顶点集 V ,边集 E
团(clique):子图,其中所有节点成对连接。一个图G中含有多个团。
极大团(maximal-clique):不能再加入任何一个顶点,使之仍为团。一个图G可以有多个极大团。
最大团(maximum-clique):子图,含顶点最多的极大团。一个图G可以有多个最大团。
对极大团的寻找,方法很多,经典的是Bron-Kerbosch方法。
Markov-Property:对图G的顶点 v 定义一个随机变量 Xv ,使之取有限状态空间 Λv 。
Local-Markov-Property:
∀Xv,p(xv|xG∖v)=p(xv|xNv) 。换句话,顶点状态,given其近邻状态,条件独立于其他顶点状态。
在图的联合分布概率严格为正时,有两个等价的Markov-property。
1)任意子图AB被S分割,其中 XA和XB,givenXS 是条件独立的。(global-MP)
2)任意两个不相连的随机变量,given其他变量,是条件独立的。(pair-MP)
3)RBM的实现
RBM在Gibbs采样下的类,parallel-tempering未实现。
https://github.com/jxyyjm/test_nn/blob/master/src/mine_rbm_all.py
reference
1. 《Training Restricted Boltzmann Machines: An Introduction》
2. 《Proof of Hammersley-Clifford Theorem》
3. 《Markov Chains: Gibbs Fields, Monte Carlo Simulation, and Queues》
4. 《Training Products of Experts by Minimizing Contrastive Divergence》
5. 《On Contrastive Divergence Learning》
6. 《Fast Algorithms for the Maximum Clique Problem on Massive Sparse Graphs》最大团在大规模离散图上的高效查找。
7. 《Continuous Restricted Boltzmann Machine with an implementable Training Algorithm》主要处理连续值的情况。