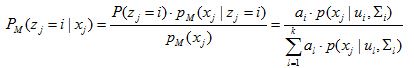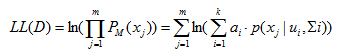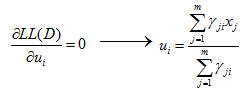高斯混合-EM算法

转自http://blog.csdn.net/lvhao92/article/details/50802703

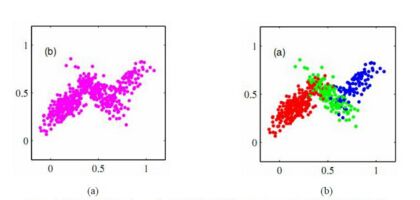
混合高斯模型(Mixture-of-Gaussian)，从这个名字上来看，就是多个高斯分布混合着叠加来模拟我们的数据分布。事实上亦是如此。

快看这一坨屎绿，恩，他就是一个单高斯模型。公式什么的都不写了吧，考研数学必考的。

我们伟大的混合高斯模型就是由一坨坨不同的单高斯模型所构成的。

如下

妈妈说，只要模型的个数足够的多，这玩意是可以逼近任何概率分布的。

恩，对模型有了大概的了解之后我们来看数学公式。

（1）

公式中ui和Ei(你懂的)就是代表的是每个高斯分布的均值和标准差。他们能确定一个独特的高斯分布。

ai是混合系数，意思就是这些不同的高斯分布究竟是怎么个混合法的才混合出这样的一个分布，其中。恩，就是个系数。

k就是表明x是由K个高斯分布每个都按照ai的系数大小混合而成的分布。

好，如果另随机变量Zj属于{1,2,…k}表示生成样本Xj的高斯混合分布，简单说，Xj不是由K个高斯分布混合而成的吗？那么Zj就是表示其中的某一个高斯分布。

所以，Zj的先验概率P(zj=i)对应的就是ai。根据贝叶斯定理，zj的后验分布对应于

（2）

这个式子第一个等号就不用废话了，典型的贝叶斯公式。第二个等式，分母部分就是等式(1)，分子部分前面红字不是说了吗，先验概率就是ai啊~

那为什么P(x|z=j)可以转化成p(x|ui,Ei)呢，因为一旦确定了高斯分布的均值和方差是可以确定一个独特的高斯分布的，如蓝字所说，而我们这里用Zj来表示其中的某个高斯分布。因此，这也是一一对应的。

好啦~我们来用γji来简单的标记Pm(zj=i|xj)（等式2,简单化标记，不然写太多），他的意思就是样本Xj由第i个高斯混合成分生成的后验概率。再简单的说，就是我看到一个样本Xj那么它由第i坨高斯分布生成的概率又是多大呢？

那么，如果我偶遇一个样本，是不是可以用上面的这个后验概率来得出他是最有可能由哪一坨高斯分布来表示的呢？或者说哪一坨高斯分布与他最接近？那我们可不可以用这个与样本最接近的高斯分布标签来对这个样本进行标定呢，那我们是不是就可以得到我们这个样本的类别啊？那这个不就是个聚类的过程吗？因为，我们是能够通过样本的自身性质来获得样本的标签。（http://blog.csdn.net/lvhao92/article/details/50788380第一篇博文有介绍）所以，这就解释了为什么我在标题加了聚类两个字

所以，高斯混合聚类将把样本集划分成K个簇（为什么是K个？因为有K坨高斯分布嘛），每个样本Xj的簇标记是如下确定：（3）

因此，从原型聚类的角度来看，高斯混合聚类是是采用概率模型（高斯分布）对原型进行刻画，簇划分则由原型对应后验概率确定。

有没有发现，我们已经可以根据当前的参数来计算了每个样本属于每个高斯成分的后验概率γji了，也就是说我们能够根据已知参数来确定未知参数(样本分类)了，如果你仔细看了我上一篇博文，你会立刻反映出来，这不就是EM算法的E步吗？是的。以上部分就是高斯混合的EM算法的E步，所以我说啊，EM算法就是个思想。k-means用到了，而这里也可以用到。接下来就是要进行我们的M步了。也就是更新模型参数，参数是什么呢，就是{ai，ui，Ei}（他们是前面的混合系数，高斯分布的均值和方差）

M步中如何更新参数呢？就是极大似然估计，关于极大似然估计，http://blog.csdn.net/lvhao92/article/details/50775860这篇博文有介绍。

好，最大化(对数)似然

（4）

恩，m代表的就是m个样本，为什么这里用的是Pm(xj)而不是前面的Pm(Zj=j|Xj)，因为毕竟我希望是多个高斯分布混合着能很好的表示我们的样本，而后者那个后验概率只是为了想给我们的样本划个类，标个记，所以才这样表示来看看究竟哪个高斯分布与样本最像，好让我们的这个样本就标为这个类。

接下来，就纯数学计算了，毕竟是求极大似然估计嘛，所以，开始对公式（4）算偏导数喽~

（5）

（6）

这里可以看到各混合成分的均值可通过样本加权平均估计，样本权重是每个样本属于该成分的后验概率。

而混合系数ai的计算要复杂点，除了最大化LL(D)，还要满足（7）。这样，求一个式子的最大值，同时有个式子要来约束，立马要反映出拉格朗日

于是乎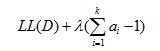，（8）。对ai求偏导，令导数为0，可得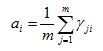（9）。即每个高斯成分的混合系数由样本属于该成分的平均后验概率所确定。

所以呢~我们的参数也是可以更新了，通过式（5）（6）（9）来分别更新ui，Ei和ai。我们的M步总算大功告成啦！

接下来就是可以愉快的和E步迭代搞基了~

（end）