Python 波形处理
使用Jupyter Notebook进行波形分析
首先拿到了振动传感器的数据
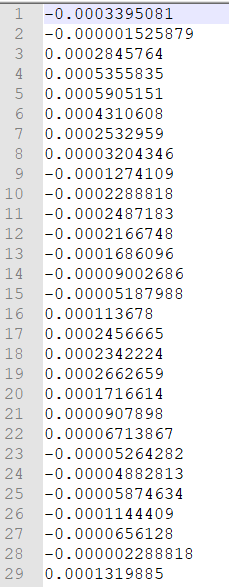
解释数据:
我们知道机械波分为横波、竖波、以及复杂波,现实世界中全部为复杂波——上下左右都有振动。
传感器每秒记录10240条数据(**每分钟仅记录前30秒的数据**),对应X轴、Y轴、以及Z轴的数据。我们这次仅分析一天 Z轴的数据。
由于一秒10240条数据一天的数据量就是
10240*30s*60min*24h = 442368000条记录,这个数据量挺大的,如果将一天的数据都画出波形图,会导致没有任何细节,整个图都会缩在一起。所以我这里先做了每分钟的均方根处理,然后每分钟去画图能够清晰的展示出每天哪个时间段有较强的振动。
--------------------------------接下来看代码以及效果----------------------------
#以下是导入的包、以及用到的方法
import numpy as np
from scipy.fftpack import fft,ifft
import matplotlib.pyplot as plt
import os
import math
#计算均方根
def get_rms(records):
"""
均方根值 反映的是有效值而不是平均值
"""
return math.sqrt(sum([x ** 2 for x in records]) / len(records))
#读取文件
def readname():
filePath = '/root/Rone/waveData/data'
name = os.listdir(filePath)
return name
接着将一天的数据上传到服务器指定的文件夹 ——计算每分钟的均方根,以及将结果保存(这里我打印了出来,个人感觉比保存到文件中更方便去处理)
#求每分钟的RMS
names = readname()
arr = []
for i in names:
tempData = np.loadtxt("/root/Rone/waveData/data/"+i)
rmsData = get_rms(tempData)
arr.append(rmsData)
print(i)
file=open('/root/Rone/waveData/resultRMS.txt','w')
file.write('\n'.join(str(arr)))
file.close()
print("=============")
for i in arr:
print(i)
下图是部分均方根的执行结果
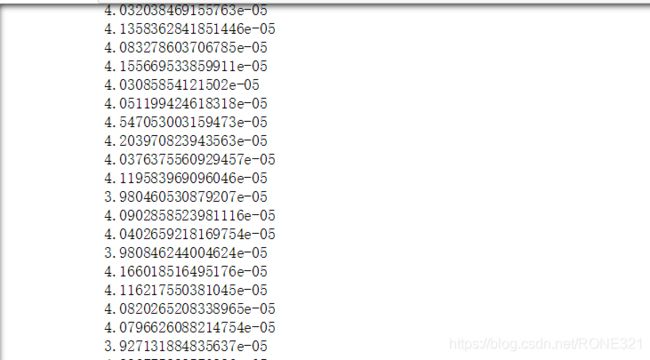 使用matlab库画出一天的均方根图
使用matlab库画出一天的均方根图
dataRMS = np.loadtxt("/root/Rone/waveData/resultRMS.txt")
x = np.linspace(0,1313,1313)
plt.subplot(4,1,1)
fig=plt.gcf()
fig.set_size_inches(128.5, 100.5)
plt.plot(x,dataRMS[0:1313])
plt.title('24h Data Analysis')
plt.xlabel('t')
plt.ylabel('x')
x2 = np.linspace(500,1313,813)
#print(x2)
print(dataRMS.size)
fig=plt.gcf()
fig.set_size_inches(20.5, 10.5)
结果图(16点——第二天14点的数据) 我们可以看出峰值高的是下午5点左右 以及第二天8-10点左右。(使用均方根后出现一个问题——没有了负值,这是因为均方根是经过平方后再开方导致的)。
我们可以看出峰值高的是下午5点左右 以及第二天8-10点左右。(使用均方根后出现一个问题——没有了负值,这是因为均方根是经过平方后再开方导致的)。均方根只会把差距放大,不能代表波形的振幅。
接下来我们就去找异常值。
#查询16点到16.30点的数据 total
names = readname()
arr = np.zeros(1)
for i in names:
tempData = np.loadtxt("/root/Rone/waveData/data/"+i)
#
#print(tempData)
arr = np.concatenate((arr,tempData),axis=0)
if i =='20190909_165228.txt':#
break;
print(i)
print(len(arr))
lenthData = len(arr)
np.savetxt(r"/root/Rone/waveData/16_17_hour.txt",arr)
x = np.linspace(0,lenthData,lenthData)
#print(x)
plt.subplot(4,1,1)
plt.plot(x,arr[0:])
fig=plt.gcf()
fig.set_size_inches(158.5, 130.5)
#查询16.30点到17.00点的数据 total
names = readname()
arr = np.zeros(1)
rootPath = "/root/Rone/waveData/data/"
# 52 58.txt
for i in (53,59):
tempData = np.loadtxt(rootPath+"20190909_16"+str(i)+"58.txt")
#
#print(tempData)
arr = np.concatenate((arr,tempData),axis=0)
if i =='20190909_170058.txt':#
break;
print(i)
print(len(arr))
lenthData = len(arr)
#np.savetxt(r"/root/Rone/waveData/16_30_17_00_hour.txt",arr)
x = np.linspace(0,lenthData,lenthData)
plt.subplot(4,1,1)
plt.plot(x,arr[0:])
fig=plt.gcf()
fig.set_size_inches(158.5, 130.5)
#查询17.00点到17.30点的数据 total
names = readname()
arr = np.zeros(1)
rootPath = "/root/Rone/waveData/data/"
# 52 58.txt
for i in range(0,9):
tempData = np.loadtxt(rootPath+"20190909_170"+str(i)+"58.txt")
arr = np.concatenate((arr,tempData),axis=0)
if i =='20190909_170958.txt':#
break;
print(i)
for i in range(10,30):
#20190909_172958
tempData = np.loadtxt(rootPath+"20190909_17"+str(i)+"58.txt")
arr = np.concatenate((arr,tempData),axis=0)
if i =='20190909_170058.txt':#
break;
print(i)
print(len(arr))
lenthData = len(arr)
#np.savetxt(r"/root/Rone/waveData/16_30_17_00_hour.txt",arr)
x = np.linspace(0,lenthData,lenthData)
#print(x)
plt.subplot(4,1,1)
plt.plot(x,arr[0:])
fig=plt.gcf()
fig.set_size_inches(158.5, 130.5)
 上图有断点数据 很大的可能是因为传感器只有每分钟前30秒的数据。
上图有断点数据 很大的可能是因为传感器只有每分钟前30秒的数据。
接着查询
#查询21.40点到22.50点的数据 total
names = readname()
arr = np.zeros(1)
rootPath = "/root/Rone/waveData/data/"
for i in range(40,41):
tempData = np.loadtxt(rootPath+"20190909_21"+str(i)+"58.txt")
arr = np.concatenate((arr,tempData),axis=0)
print(i)
#lenthData = len(arr)
lenthData = 10240
x = np.linspace(0,1,10240)
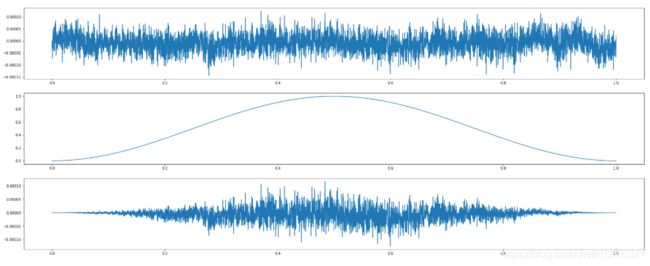
#原始波形
plt.subplot(4,1,1)
plt.plot(x,arr[0:10240])
#加窗
w = np.hanning(10240)
plt.subplot(4,1,2)
plt.plot(x,w)#画出 hanning窗
z = w*arr[0:10240]
plt.subplot(4,1,3)
plt.plot(x,z)#加hanning窗后的波形
fig=plt.gcf()
fig.set_size_inches(30.5, 16.5)
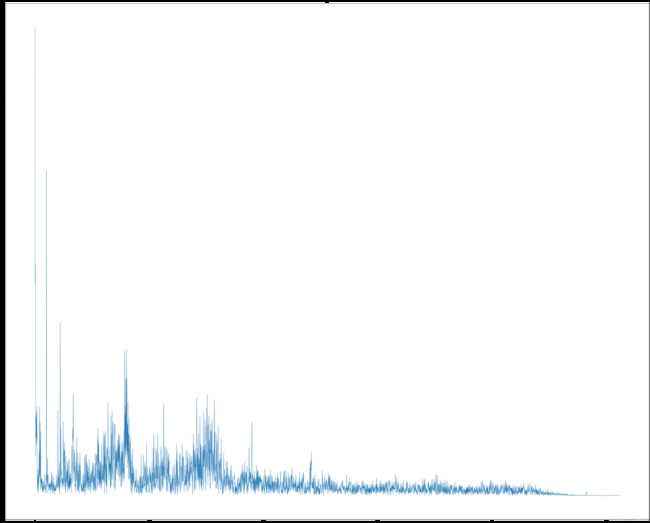
yf1=abs(fft(z[0:])) #归一化处理
yf2 = yf1[range(5120)] #由于对称性,只取一半区间
xf = np.arange(5120)
plt.subplot(222)
plt.plot(xf[0:],yf2[0:])
plt.title('FFT',fontsize=12)
fig=plt.gcf()
fig.set_size_inches(158.5, 130.5)