推荐系统(二):PNN源论文整理和思考
文章目录
- 一、背景
- 二、PNN思想和模型
- 三、优化
- 四、代码实践。
- 参考文献
一、背景
PNN源论文为《Product-based Neural Networks for User Response Prediction》,是上海交大团队发表在ICDM 2016上。本文在阅读源论文和网上其它资料的基础上,重点整理了论文的细节和思想。
我们已经知道,在信息检索领域(IR,Information Retrieval),比如在推荐系统和广告场景中,个性化推荐是一类非常重要的任务。在这类场景中,存在着许多类别特征,如用户所在的城市,性别等。对于类别型特征的充分学习,对于高的CTR来说(模型更好的学习能力)来说,是十分重要的。
在PNN之前,已经存在了许多模型,如Logistic Regression、GBDT、FM,但都存在一些不足,如LR和GBDT非常依赖人工特征工程,FM则缺少对高阶组合特征的建模,仅仅对特定阶的组合特征建模。
随着DNN在图像处理、语音识别、自然语言处理领域的不断应用,将DNN应用于CTR预估或者推荐系统的研究逐渐多了起来。我们知道,DNN的输入往往是dense real vector, 但是类别型特征ont-hot之后是高维且稀疏的。那么,常见的做法是通过加入Embedding Layer将输入映射到低维度的Embedding空间中。FNN(参考文献2)使用FM初始化embedding vector,同时也受限于FM(无法避免FM的弊端,即只能对特定阶的组合进行学习);CCPM(参考文献5)利用CNN卷积来学习组合特征,但是只在相邻的特征间卷积,没有考虑到非相邻的特征的组合。
二、PNN思想和模型
因此,基于上述的分析,PNN应运而生。PNN总体的思想是利用Embedding Layer来处理类别特征,利用Product Layer来学习二阶特征,利用Full-connect Layer学习高阶特征。
也就是说,PNN宏观上来看包括三层:Embedding Layer、Product Layer、Full-connect Layer。最开始的输入太稀疏维度太高,没法直接放到DNN中去学习,所以比较通用的做法就是通过Embedding到一个低维的稠密的实数向量中,作为原始特征的在Embedding空间中的表示。然后PNN利用Product Layer来学习filed(在论文中,一个类别型特征就是一个field)之间的交互特征,这也就引入了非线性的组合特征。可以采用内积、外积、内积+外积(由此,引入了3种PNN)的形式。最后利用全连接层充分的学习高阶组合特征,并得到最终CTR预测概率。
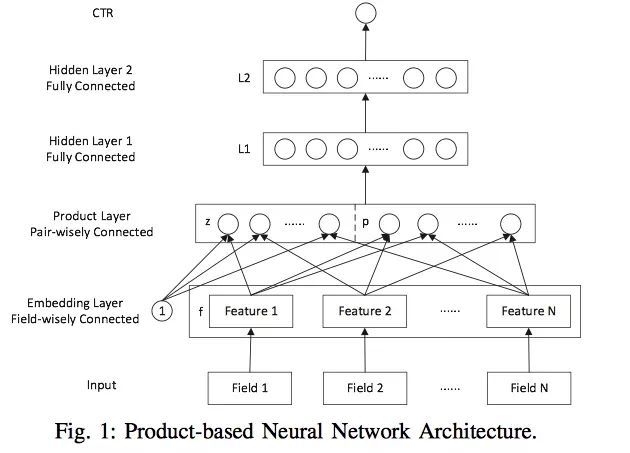
PNN的结构图如下:
(1)Input: 一个Field就是一个类别型特征。注意:上图中的Input是one-hot之后的,而且只给出了类别型特征。所以每个Field i i i都是一个向量,向量的大小就是类别型特征one-hot之后的维度,即不同Field的维度是不同的。
(2)Embedding Layer: Embedding是Field-wisely Connected,就是一个Field只与一个embedding关联,Field之间网络的权重毫无关系(看箭头)。而且只有权重,没有bias。一个Field经过嵌入后,得到一个Feature,也就是对应的Embedding Vector嵌入向量。其维度一般是预先设定好的定值,论文中采用的是10。也就说是不同Feature的维度都是一样的。
(3)Product Layer: 这是本文的重点阐述的内容,需要仔细阅读,重点观察Embedding Layer到Product Layer箭头的指向。
我们先看网络结构,Product Layer分为两部分,一部分叫做z,一部分叫做p。我们说下结论:
- 先看z,z中每个圈都是一个向量,向量大小为Embedding Vector大小,向量个数 = Field个数 = Embedding向量的个数。
- 再看p,Product Layer中如果是内积,p中每个圈都是一个值;如果是外积,p中每个圆圈都是一个二维矩阵。(内积和外积的知识请参考文献4)
那么问题来了,z中是向量,p是值或矩阵。矩阵和向量怎么拼在一起训练呢?这个问题我们接下来会说。
继续看Product layer,可以看到Embedding Layer中的存在一个1,其实就是直接把Embedding Vector直接拿来没进行变换。这样做处理起来很简单,但是可能也有个缺点。即当Embedding Vector和p的数值分布差异交大,导致分布不稳定不利于训练。
那z中的“圆圈”怎么来的呢?在数据流中,假设Field个数为 N N N,那么经过Embedding后的Field得到了 N N N个Feature,即 N N N个嵌入向量。这 N N N个嵌入向量直接拿过来并排放到z中就是z。这部分代表的是对低维度特征,或者说原始特征的建模。
那p中的“圆圈”怎么来的呢?然后,针对这 N N N个嵌入向量,两两组合进行Product operation(仔细看箭头),把结果放到一起就得到了p。首先, N N N个向量两两组合,会产生 N ( N − 1 ) / 2 N(N-1)/2 N(N−1)/2对组合,这就是p中圆圈的个数,或者说神经元的个数。如果是内积运算,那么每个神经元就是一个实数值;如果进行外积运算,那么每个神经元就是一个二维矩阵。
这就是Product Layer。当然,我们还有个问题没解决,即如果采用外积,矩阵和向量怎么拼在一起训练呢?在论文中,针对外积产生的每一个二维矩阵,我们都通过另外一个矩阵 W W W,大小为 M ∗ M M*M M∗M(M就是embedding的维度)。这两个矩阵对应位置相乘,再相加,就得到了最终的结果。
参考文献3中有个图,逻辑很清晰:
假设两个嵌入向量,列向量 U U U, V V V。 ⊙ ⊙ ⊙表示对应位置相乘,然后再相加的操作。 U V UV UV的外积结果为二维矩阵。那么有公式:
U V T ⊙ W = U T W V UV^T⊙W=U^TWV UVT⊙W=UTWV
等式右边比左边的复杂度要低一些。公式可以这样理解:外积与参数矩阵相乘,相当于对 U U U经过 W W W矩阵投影,在投影空间中与 V V V计算内积。是一个非常有用的trick。
另外,如果Product Layer使用内积运算,那么就是IPNN。p中每个神经元都是一个实数值,和z中的嵌入向量拼接起来,传入神经网络即可。如果Product Layer使用外积运算,就得到OPNN。如果Product Layer同时使用内积+外积,把内积和外积的结果拼接起来,就得到PNN*。
(4)Hidden Layer 1:
从图中可以看到,这是一个简单的全连接层:
l 1 = r e l u ( l z + l p + b 1 ) \bm{l}_1 = relu(\bm{l}_z+\bm{l}_p+\bm{b}_1) l1=relu(lz+lp+b1)
其中,我们设定 l z \bm{l}_z lz, l p \bm{l}_p lp, b 1 \bm{b}_1 b1均为 D 1 D_1 D1。
(5)Hidden Layer 2:
接入Hidden Layer 1的输出后,Hidden Layer 2也是一个全连接层:
l 2 = r e l u ( W 2 ∗ l 1 + b 2 ) \bm{l}_2 = relu(\bm{W}_2*\bm{l}_1+\bm{b}_2) l2=relu(W2∗l1+b2)
(6)CTR:
这一层也比较简单:
y ^ = σ ( W 3 ∗ l 2 + b 3 ) \hat{y} = \sigma(\bm{W}_3*\bm{l}_2+\bm{b}_3) y^=σ(W3∗l2+b3)
当然,由于解决的问题是二分类,所以损失函数自然是逻辑损失函数:
L ( y , y ^ ) = − { y l o g y ^ + ( 1 − y ) l o g ( 1 − y ^ ) } L(y,\hat{y} )=-\left\{ylog\hat{y}+(1-y)log(1-\hat{y})\right\} L(y,y^)=−{ylogy^+(1−y)log(1−y^)}
三、优化
PNN原始的论文中,针对外积部分每两个嵌入向量组合,一共有 N ( N − 1 ) / 2 N(N-1)/2 N(N−1)/2这么多对组合。这个复杂度是 O ( N 2 ) O(N^2) O(N2)的,论文中通过下面的公式进行了化简:
其中的 f i f_i fi就是嵌入向量。也就是说先把所有的嵌入向量相加求和,然后再和自己进行外积。得到一个 ( N , N ) (N,N) (N,N)的外积矩阵。然后再和 D 1 D_1 D1个不同的 W W W进行对应位置相乘相加的操作,就得到了最后隐藏层输入的 D 1 D_1 D1个值。
这里的优化主要是把嵌入向量的 N ( N − 1 ) / 2 N(N-1)/2 N(N−1)/2个组合对,优化成了1个,即把平方的复杂度降低到线性的。
但是,这一部分的优化其实没必要。因为即使是 N N N平方的复杂度,但是每两个嵌入向量进行外积的计算完全可以并行化。其实是可以接受的,所以现在已经去掉了。
关于新的文章的扩展版,请参考文献6。
四、代码实践。
论文原作者开源了PNN的代码,请参考作者的github。地址。
参考文献
【1】PNN: Product-based Neural Networks for User Response Prediction
【2】FNN: Deep learning over multi-field categorical data: A case study on user response prediction
【3】计算广告CTR预估系列(八)–PNN模型理论与实践
【4】CTR 预测理论(二十五):矩阵和向量乘法总结
【5】CCPM:A convolutional click prediction model,
【6】Product-based Neural Networks for User Response Prediction over Multi-field Categorical Data