1、初级算法题:旋转数组
题目:给定一个数组,将数组中的元素向右移动n个位置,其中n是非负数。
输入:[1, 2, 3, 4, 5, 6, 7]和n=3
输出:[5, 6, 7, 1, 2, 3, 4]
提示:
向右旋转1步:[7, 1, 2, 3, 4, 5, 6]
向右旋转2步:[6, 7, 1, 2, 3, 4, 5]
向右旋转3步:[5, 6, 7, 1, 2, 3, 4]
假设,给定数组[8, 7, 6, 5, 4, 3, 2, 1],n为3,则我们可以通过n将该数组分成以下两部分:
划分的规则如下:
-
left部分的数组元素只需右移n个位置即可。
-
right部分的数组元素如果右移n个位置就会越过数组边界,因此需要在数组中循环到最左侧。
而划分的位置则是:数组长度 - n。
因此,可以得到下面三种解法。
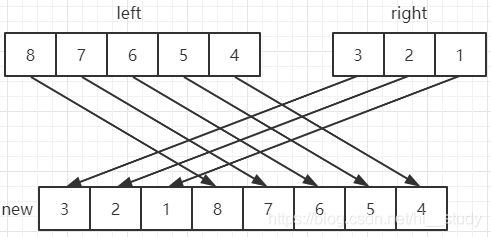
1、使用新数组存放变换后的left、right
在不考虑空间占用的情况下,则很容易解决问题,只需一个与给定数组等长的数组,将left、right部分的元素经过右移n次的转换,放到新数组即可,如下图:
代码如下:
public static int[] doScroll(int[] datas, int step) {
int length = datas.length;
int[] result = new int[length];
int right = step % length;
if (right == 0) {
return datas;
}
// 将left部分移动到新数组
int left = length - right;
for (int i = 0; i < left; i++) {
result[right + i] = datas[i];
}
// 将right部分移动到新数组
for (int i = 0; i < right; i++) {
result[i] = datas[left + i];
}
return result;
}
测试代码:
public static void main(String[] args) {
int[] original = { 8, 7, 6, 5, 4, 3, 2, 1 };
int[] update = doScroll(original, 3);
System.out.println(Arrays.toString(update));
}
结果如下:
[3, 2, 1, 8, 7, 6, 5, 4]
2、将left的元素交换到right的右侧
如果要尽量的少使用额外的存储空间,则上一个方法就不可行了。因此,我们只能在该数组空间做文章了。
这样,就涉及到元素的交换。我的想法如下:
①、还是像最上面那样,将数组分成left、right两部分,如下图:
②、从left最右侧取出一个元素,放在right最左侧,如下图:
③、让该元素在right中右移n个位置,即不断地和其右侧元素交换位置,n次,如下图:
重复上述②、③动作,直至left中没有元素,即数组索引为0,则数组旋转完成。
代码如下:
public static void doScroll(int[] datas, int step) {
int length = datas.length;
int n = step % length;
if (n == 0) {
return;
}
// left与right的分界点,right包含point点
int point = length - n;
// 从left取其右端的元素
for (int left = point - 1; left >= 0; left--) {
// 让left右端的元素与right中的元素交换n次位置
for (int right = left; right < left + n; right++) {
int tmp = datas[right + 1];
datas[right + 1] = datas[right];
datas[right] = tmp;
}
}
}
测试代码:
public static void main(String[] args) {
int[] original = { 8, 7, 6, 5, 4, 3, 2, 1 };
doScroll(original, 3);
System.out.println(Arrays.toString(original));
}
结果如下:
[3, 2, 1, 8, 7, 6, 5, 4]
3、先整体反转,再部分反转
这道算法题我是在头条号【蜜蜂攻城狮】的视频中看到的,他还介绍了一种方法,我觉得挺巧妙的,特此记录下。
该方法的思想如下:
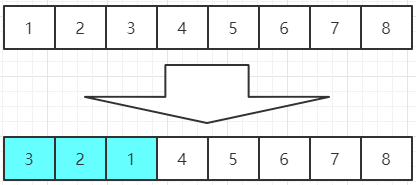
①、将数组的元素整体反转,如下图:
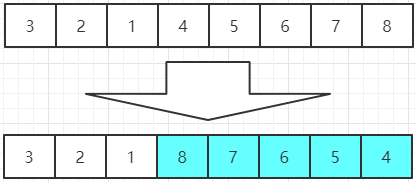
②、在①的结果中将前n项的元素反转,如下图:
③、在②的结果中将后(数组长度 - n)项的元素反转,如下图:
代码如下:
public static void doScroll(int[] datas, int step) {
int n = step % datas.length;
// 反转数组整体
reverse(datas, 0, datas.length - 1);
// 反转前n项
reverse(datas, 0, n - 1);
// 反转后length - n项
reverse(datas, n, datas.length - 1);
}
public static void reverse(int[] datas, int start, int end) {
int left = start, right = end, tmp = 0;
while (left < right) {
tmp = datas[left];
datas[left] = datas[right];
datas[right] = tmp;
left++;
right--;
}
}
测试代码:
public static void main(String[] args) {
int[] datas = { 8, 7, 6, 5, 4, 3, 2, 1 };
doScroll(datas, 3);
System.out.println(Arrays.toString(datas));
}
结果如下:
[3, 2, 1, 8, 7, 6, 5, 4]
暂时就想到这么多了,欢迎大家补充。