java 数据结构 栈的应用 数学表达式计算

假如我们现在输入了一个数学表达式(52-50)*3-5*8
要写个程序得出结果.单纯的四则运算肯定是不行的.
我们把上述表达式叫做标准表达式或者中缀表达式,
有一中记法叫后缀记法或者逆波兰记法：
中缀表达式：(52-50)*3-5*8
后缀式:52 50 - 3 * 5 8 * -
那么这个后缀式我们如何得到结果呢.我们得使用栈，步骤如下:

• 遇到数字直接入栈,所以52, 50都入栈
• 遇到表达式就把栈中2个数字弹出,然后与表达式计算出结果,在把结果压入栈,所以我们把52,50弹出栈,把52-50,结果2压入栈中
• 遇到数字3,直接进栈,此时栈中是2和3
• 遇到乘号,把2,3弹出,将2*3=6，把6压入栈
• 在遇到5,8，压入栈中,此时栈中是6,5,8
• 遇到乘号,将5,8弹出,把结果40压入栈中
• 最后遇到-号，将6,40弹出,计算6-40得到结果-34

所以我们现在可以利用栈结果计算一个后缀式了，我们现在的问题就是把一个中缀式转换成后缀式，答案是也用栈结构,举个列子:

中缀表达式：3-2*2*(1+2)
后缀式:3 2 2 * 1 2 + * -
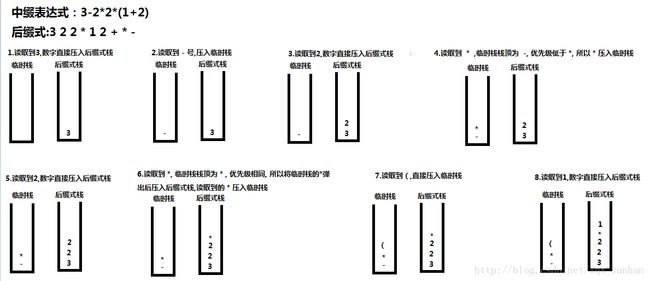
要想把上述的中缀表达式转换为后缀表达式,步骤如下(我们用一个临时栈来装元素,用一个后缀式栈来装结果):

• 读取到数字,所以3,直接压入后缀式栈
• 读取到减号,我们压入临时栈
• 继续读取到数字2,直接压入后缀式栈
• 继续读到乘号,我们开临时栈栈顶为减号,减号优先级比乘号低,所以乘号也压入临时栈,此时临时栈里有-, * 后缀式栈有 3, 2
• 继续读到数字2，直接压入后缀式栈
• 在读到乘号,这时临时栈栈顶也为乘号,两个操作符优先级相等,我们把临时栈栈顶的乘号弹出压入后缀式栈,然后将读到的乘号压入临时栈.此时后缀式栈为3 2 2 * 临时栈为 - *
• 读到左大括号，我们直接将其压入临时栈,这是临时栈为- * (
• 读到1,压入后缀式栈,这时后缀式栈为3 2 2 * 1
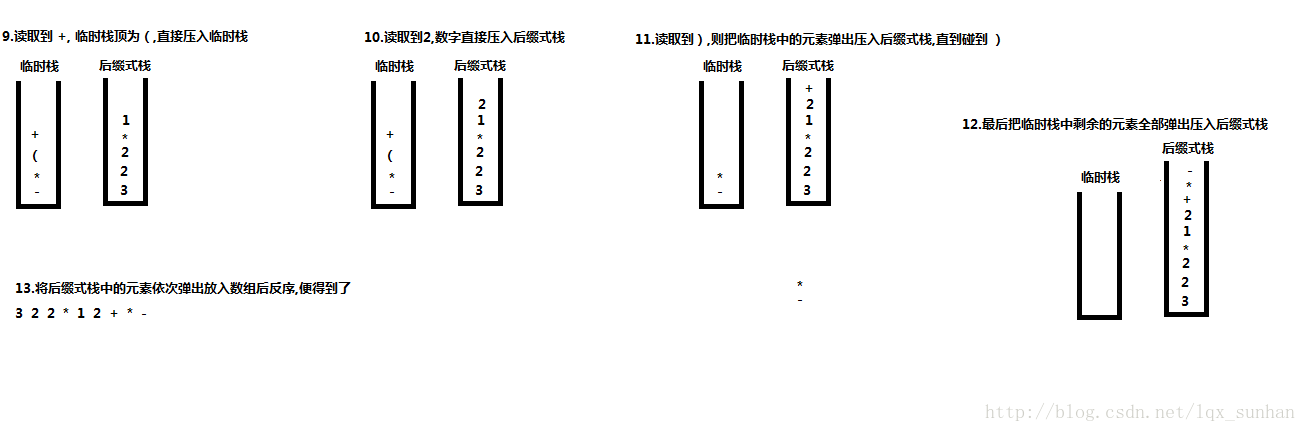
• 读到加号,我们看临时栈栈顶为左大括号,所以直接将加号压入临时栈,这是临时栈为 - * ( +
• 读到2，压入后缀式栈,此时后缀式栈为 3 2 2 * 1 2
• 最后读到右大括号,这时将临时栈的符号依次弹出压入后缀式栈,直到碰到左大括号,这时临时栈为 - ,后缀式栈为 3 2 2 1 2 +
• 然后将临时栈中剩余的元素弹出,压入后缀式栈,这时临时栈空了,后缀式栈为 3 2 2 * 1 2 + * -

以上中缀式转后缀式的过程可能有点绕,接下来我画图来解释一下这个过程,这个过程其实有几个要点:

1. 当临时栈栈顶元素优先级低于刚刚读取到的元素时,把刚读取的元素压入临时栈
2. 当临时栈栈顶元素优先级高于刚刚读取到的元素时,一直弹出栈顶的元素,直到栈顶元素的优先级低于刚读取的那个元素，然后将刚读取的那个元素压入临时栈
3. 当栈顶元素优先级等于刚读取的元素时,弹出栈顶元素,然后将刚读取的元素压进去
4. 当读取到一个数字时,不用进行任何操作,直接压入后缀式栈

5. 当栈顶是左大括号”(“时,直接将读取到的元素压入临时栈

   图解:
   图1:
   

   图2:
   

接下来我们上代码,代码中使用的栈是我另一篇博客中实现的栈:
链接: http://blog.csdn.net/lqx_sunhan/article/details/79051964

代码

package test;

import collection.MyStackLink;

import java.util.Scanner;
import java.util.regex.Matcher;
import java.util.regex.Pattern;

/**
 * Created by sunhan on 2018/1/13.
 */
public class suffixTest {

    public static void main(String args[]) {

        /**
         * 用于临时存放操作符的栈
         */
        MyStackLink operatorStack = new MyStackLink();

        /**
         * 存放最后的后缀表达式的栈
         */
        MyStackLink temp = new MyStackLink();


        Scanner sc = new Scanner(System.in);
        System.out.println("请输入数学表达式(目前支持带小括号的四则运算):");
        String next = sc.next();
        while(next.length() != 0){
            /**
             * 按照给定的正则表达式切割字符串
             */
            String[] split = split(next, "\\d+", "[\\+\\-\\*\\/]", "\\(", "\\)");
            /**
             * 新的字符串赋值
             */
            next = split[1];

            /**
             * 刚刚切割出来的元素
             */
            String element = split[0];


            // 判断是否是一个小数或者整数(test为自己写的方法)
            boolean test = test(element, "-?\\d*.?\\d+");

            if (test) {
                // 是一个数字,则直接入栈
                temp.push(element);
                continue;
            }
            /**
             * 如果是右大括号则把操作符的栈中的操作符依次弹出直到遇见左大括号
             */
            if (element.equals(")")) {
                boolean flag = false;
                // 如果碰到)，则将栈中元素全部弹出,依次压入临时栈,直到碰上(,若栈空也没有(则报错
                while (!operatorStack.isEmpty()) {
                    if (operatorStack.top().toString().equals("(")) {
                        flag = true;
                        operatorStack.pop();
                        break;
                    }
                    temp.push(operatorStack.pop());
                }
                if (!flag) {
                    throw new RuntimeException("表达式非法");
                }
                continue;
            }

            /**
             * 如果是操作符栈是空的则直接进栈
             */
            if (operatorStack.isEmpty()) {
                operatorStack.push(element);
            } else {
                /**
                 * 这里是一个重点
                 * comparePriority是比较表达式优先级的方法
                 * 我们拿到栈顶元素与刚刚输入的元素的优先级后进行以下操作
                 * compare==3代表栈顶是(,这时我们输入的元素直接入栈
                 * compare==1说明栈顶的优先级较高，这是我们会一直把栈顶元素弹出放进temp的栈,知道栈顶元素优先级更低
                 * compare==0说明优先级相等,直接将栈顶元素弹出放入temp栈,然后将输入的元素压入操作符栈顶
                 * compare==-1说明栈顶优先级较低,直接将输入的元素压入栈顶
                 */
                // 栈顶
                String topStack = operatorStack.top().toString();
                // 比较优先级
                int compare  = comparePriority(topStack, element);
                if(compare == 3){
                    // 如果栈顶是(,则直接进栈
                    operatorStack.push(element);
                } else if (compare == 1) {
                    // 栈顶优先级高,则弹出栈,进入后缀表达式栈,直到栈顶优先级更低或栈空,然后将next压入操作符栈
                    while(compare != -1) {
                        operatorStack.pop();
                        temp.push(topStack);
                        if(operatorStack.isEmpty()){
                            break;
                        }
                        topStack = operatorStack.top().toString();
                        compare = comparePriority(topStack, element);
                    }
                    operatorStack.push(element);
                } else if (compare == 0) {
                    // 优先级相等, 则弹出栈,进入后缀表达式栈,然后将next压入操作符栈
                    operatorStack.pop();
                    operatorStack.push(element);
                    temp.push(topStack);
                } else {
                    // 栈顶优先级低,直接将next压入栈
                    operatorStack.push(element);
                }
            }
        }

        /**
         * 完成后,我们把操作符栈中剩余的元素全部弹出放进后缀表达式(temp)栈
         */
        // 一直到栈空,弹栈,将弹出的元素压入temp栈
        while(!operatorStack.isEmpty()){
            Object pop = operatorStack.pop();
            temp.push(pop);
        }

        // 用于装整个后缀表达式的数组,我们之后会进行反序操作,因为我们后缀表达式栈中的后缀表达式按照pop的顺序依次弹出后顺序是相反的
        String[] s = new String[temp.size()];
        int count = 0;
        while(!temp.isEmpty()){
            Object pop = temp.pop();
            s[count++] = pop.toString();
        }


        /************************ 至此后缀表达式已经转换完成 **************************/


        // 数组反序
        Object[] reverse = reverse(s);

        /**
         * 以下是计算一个后缀表达式的过程
         * 原理是:
         * 依次读取每个元素
         * 1.是数字  则直接入栈
         * 2.是操作符  则弹栈2次,拿到2个元素,将他们与这个操作符计算得到结果后,把结果压入栈中
         * 3.直到最后,栈顶将会是结果
         */
        MyStackLink calculateStack = new MyStackLink();

        for(Object o : reverse){
            String data = o.toString();
            boolean isNumber = test(data, "-?\\d*.?\\d+");
            if(isNumber){
                // 是数字则入栈
                calculateStack.push(Float.parseFloat(data));
            } else {
                // 不是数字则弹出2个栈顶元素,用这个表达式进行计算,在压入栈顶
                float secondNum = (float) calculateStack.pop();
                float firstNum = (float) calculateStack.pop();
                float r = calculate(data, firstNum, secondNum);
                calculateStack.push(r);
            }
        }

        System.out.println("result: " + calculateStack.pop());
    }

    /**
     * 将2个数字进行四则运算
     * @param operator
     * @param firstNum
     * @param secondNum
     * @return
     */
    private static float calculate(String operator, float firstNum, float secondNum){
        float r = 0;
        switch (operator){
            case "+":
                r = secondNum + firstNum;
                break;
            case "-":
                r = firstNum - secondNum;
                break;
            case "*":
                r = firstNum * secondNum;
                break;
            case "/":
                r = firstNum / secondNum;
                break;
            default:
                r = 0;
        }
        return r;
    }

    /**
     * 正则测试
     * @param src 进行测试的字符串
     * @param regx 正则表达式
     * @return
     */
    private static boolean test(String src, String regx){
        Pattern p = Pattern.compile(regx);
        Matcher matcher = p.matcher(src);
        boolean matches = matcher.matches();
        return matches;
    }


    /**
     * 比较优先级的方法,若src优先级大于tar，将返回1
     * 优先级相等返回0
     * src优先级小与tar 返回-1
     * src为)时,返回2
     * src为(时,返回3
     *
     * @param src
     * @param tar
     * @return
     */
    private static int comparePriority(String src, String tar) {
        if (src.equals("(")) {
            return 3;
        }
        if (src.equals("*") || src.equals("/")) {
            if (tar.equals("*") || tar.equals("/")) {
                return 0;
            }
            if(tar.equals("+") || tar.equals("-")){
                return 1;
            }
        }
        if(src.equals("+") || src.equals("-")){
            if(tar.equals("+") || tar.equals("-")){
                return 0;
            }
        }
        return -1;
    }

    /**
     * 数组反序
     * @param src
     * @return
     */
    private static Object[] reverse(Object[] src){
        Object[] tar = new Object[src.length];

        for(int i = src.length - 1, m = 0; i >= 0; i--, m++){
            tar[i] = src[m];
        }
        return tar;
    }
    /**
     * 将目标字符串逐个分割
     * @param src 目标字符串
     * @param regx 正则
     * eg:
     * 若目标字符串str是52+2*(3+2)
     * 我们使用代码
     *  while(str.length != 0){
     *      String[] r = split(str, "\\d+", "[\\+\\-\\*\\/]", "\\(", "\\)");
     *      r[0]依次是 52  +  2  *  (  3  +  2  )
     *  }
     * @return 返回的数组中 str[0]是替换掉的字符串  str[1]是新的目标字符串
     */
    private static String[] split(String src, String... regx){
        String[] result = new String[2];
        for(int i = 0; i < regx.length; i++) {
            Pattern p = Pattern.compile(regx[i]);
            Matcher m = p.matcher(src);
            if(m.find()){
                String group = m.group();
                if(!src.startsWith(group)){
                    continue;
                }
                String r = src.replaceFirst(regx[i], "");
                result[0] = group;
                result[1] = r;
                return result;
            }
        }
        return null;
    }
}

运行结果