二叉树的三种遍历方式java实现

二叉树的定义

 

    二叉树(binary tree)是结点的有限集合，这个集合或者空，或者由一个根及两个互不相交的称为这个根的左子树或右子树构成. 

  从定义可以看出，二叉树包括：1.空树 2.只有一个根节点 3.只有左子树   4.只有右子树  5.左右子树都存在    有且仅有这5中表现形式      

                               

二叉树与一般树的区别

一般树的子树不分次序，而二叉树的子树有左右之分.

由于二叉树也是树的一种，所以大部分的树的概念，对二叉树也适用.

二叉树的存贮：每个节点只需要两个指针域（左节点，右节点）,有的为了操作方便也会 增加指向父级节点的指针，除了指针域以外，还会有一个数据域用来保存当前节点的信息

 

二叉树的特点：

性质1：在二叉树的第i层上至多有2^(i-1)个节点(i >= 1)

性质2：深度为k的二叉树至多有2^(k-1)个节点(k >=1)

性质3：对于任意一棵二叉树T而言，其叶子节点数目为N0,度为2的节点数目为N2，则有N0 = N2 + 1。

性质4：具有n个节点的完全二叉树的深度 。

 

二叉树的遍历

二叉树的遍历分为三种：前序遍历 中序遍历 后序遍历

 

前序遍历：按照“根左右”,先遍历根节点，再遍历左子树 ，再遍历右子树

中序遍历：按照“左根右“,先遍历左子树，再遍历根节点，最后遍历右子树

后续遍历：按照“左右根”，先遍历左子树，再遍历右子树，最后遍历根节点 

其中前，后，中指的是每次遍历时候的根节点被遍历的顺序 

时间复杂度

二叉树的四种遍历方式分别是：先序、中序、后序和层次。

它们的时间复杂度都是O(n)，因为它们只访问每个节点一次，不存在多余的访问。

二叉树遍历：

前根左右

中左根右

后左右根

==================================================================

二叉树遍历的java实现

import java.util.List;
import java.util.ArrayList;

    public class Tree {

        private Node root;
        private List list = new ArrayList();

        public Tree() {
            init();
        }
        //定义节点类：
        private class Node {
            private String data;
            private Node lchid;//定义指向左子树的指针
            private Node rchild;//定义指向右子树的指针

            public Node(String data, Node lchild, Node rchild) {
                this.data = data;
                this.lchid = lchild;
                this.rchild = rchild;
            }
        }
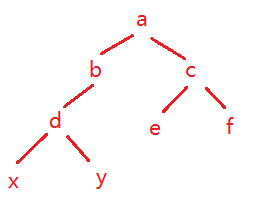
        //树的初始化:先从叶节点开始,由叶到根
        public void init() {
            Node x = new Node("X", null, null);
            Node y = new Node("Y", null, null);
            Node d = new Node("d", x, y);
            Node e = new Node("e", null, null);
            Node f = new Node("f", null, null);
            Node c = new Node("c", e, f);
            Node b = new Node("b", d, null);
            Node a = new Node("a", b, c);
            root = a;
        }

        /**
         * 对该二叉树进行前序遍历 结果存储到list中 前序遍历:ABDXYCEF
         */
        public void preOrder(Node node) {

            list.add(node); //先将根节点存入list
            //如果左子树不为空继续往左找，在递归调用方法的时候一直会将子树的根存入list，这就做到了先遍历根节点
            if (node.lchid != null) {
                preOrder(node.lchid);
            }
            //无论走到哪一层，只要当前节点左子树为空，那么就可以在右子树上遍历，保证了根左右的遍历顺序
            if (node.rchild != null) {
                preOrder(node.rchild);
            }
        }

        /**
         * 对该二叉树进行中序遍历 结果存储到list中，中序结果XdYbaecf
         */
        public void inOrder(Node node) {
            if (node.lchid != null) {
                inOrder(node.lchid);
            }
            list.add(node);
            if (node.rchild != null) {
                inOrder(node.rchild);
            }
        }

        /**
         * 对该二叉树进行后序遍历 结果存储到list中，后续结果：XYdbefca
         */
        public void postOrder(Node node) {
            if (node.lchid != null) {
                postOrder(node.lchid);
            }
            if (node.rchild != null) {
                postOrder(node.rchild);
            }
            list.add(node);

        }

        /**
         * 返回当前数的深度
         * 说明:
         * 1、如果一棵树只有一个结点，它的深度为1。
         * 2、如果根结点只有左子树而没有右子树，那么树的深度是其左子树的深度加1；
         * 3、如果根结点只有右子树而没有左子树，那么树的深度应该是其右子树的深度加1；
         * 4、如果既有右子树又有左子树，那该树的深度就是其左、右子树深度的较大值再加1。
         *
         * @return
         */
        public int getTreeDepth(Node node) {

            if (node.lchid == null && node.rchild == null) {
                return 1;
            }
            int left = 0, right = 0;
            if (node.lchid != null) {
                left = getTreeDepth(node.lchid);
            }
            if (node.rchild != null) {
                right = getTreeDepth(node.rchild);
            }
            return left > right ? left + 1 : right + 1;
        }


        //得到遍历结果
        public List getResult() {
            return list;
        }

        public static void main(String[] args) {
            Tree tree = new Tree();
            System.out.println("根节点是:" + tree.root);
            tree.preOrder(tree.root);
            //tree.postOrder(tree.root);
            for (Node node : tree.getResult()) {
                System.out.println(node.data);
            }
            System.out.println("树的深度是" + tree.getTreeDepth(tree.root));

        }
    }