二分图的最大匹配算法
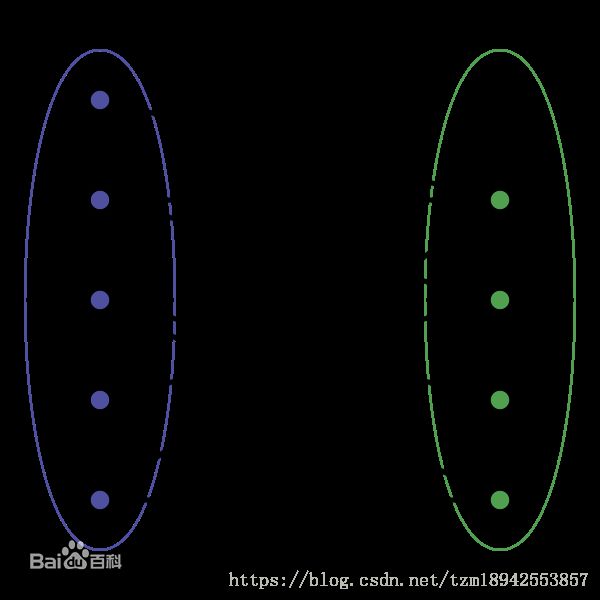
二分图的概念:二分图是图中的一种特殊模型,如果图的顶点v可以分割成两个互不相交的子集(A,B),并且图中的每条边(i,j)所关联的两个顶点i和j分别属于这两个不同的顶点集(i in A,j in B),则该图G成为一个二分图。
二分图如下:
本文通过一个问题来引出二分图的最大匹配算法 。以素数伴侣的题目为例:若两个正整数的和为素数,则这两个数称为素数伴侣,设计程序从已有的N个正整数中挑出若干个对数组成素数伴侣,问最多能挑多少对?
分析:偶数除了2以外都不为素数,而两个偶数之和与两个奇数之和都为偶数。则仅有奇数和偶数才能组成素数伴侣。则为了解决该问题我们将奇数分为一类,偶数分为一类,若在两类中元素之和为素数则在两类之间连接一根线,解决该问题就是求出最多连线的组合即可。两类元素则可认为是一个二分图,使用匈牙利算法可以很好的解决这个问题。
匈牙利算法介绍如下,但是在介绍匈牙利算法前必须了解增广路,匹配边,未匹配边,匹配点,未匹配点的概念。匹配边就是在二分图中在两个点集之间连接的边,匹配边两端都是匹配点。未匹配边是在二分图中在两个点集之间连接的边,未匹配边一端是未匹配点一端是匹配点。增广路就是在二分图中从未匹配点开始,按照未匹配边,匹配边交替的模式找到一个未匹配点结束。在这里请仔细思考一下:找到未匹配点代表什么?
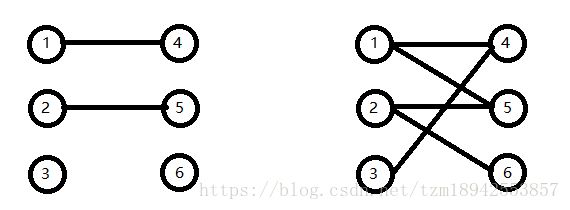
如果走增广路找到一个未匹配点之后,我们将增广路之中的匹配边断开。则第一个未匹配点与第一个匹配点构成一条匹配边。第二个匹配点与最后一个未匹配点构成第二条匹配边。就意味着我们找到了一条匹配边。
如下图:
图中1-4之间的边是匹配边,顶点是匹配点。2-5之间的变是匹配边,顶点是匹配点。则我们现在从未匹配点出发寻找一条增广路,从顶点3出发,按照未匹配边,匹配边的模式寻找增广路。3-4未匹配边,4-1匹配边,1-5未匹配边,5-2匹配边,2-6未匹配边,6为未匹配点,找到一条增广路。将匹配边断开,会发现图中多了一条匹配边,如下:
上图完成了一个二分图的最大匹配。
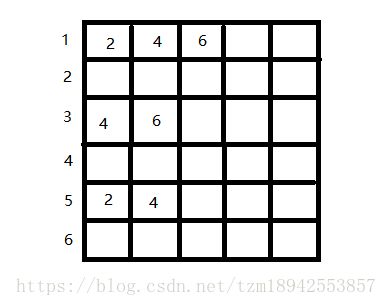
在解决素数伴侣的问题当中,首先将输入的数按照奇数偶数分好类,将能够构成素数伴侣的奇偶数对,将偶数存入一个二维数组中,偶数所在的行为与之匹配的奇数。也就是与一个奇数相匹配构成素数伴侣的偶数全都放在二维数组该奇数对应的行中。如下图:
奇数1匹配2,4,6;奇数3匹配4,6;奇数5匹配2,4。
在二维数组中寻找增广路:
初始化素数伴侣对数,初始化素数伴侣中与偶数匹配的前一奇数伴侣的数组pre为0,若pre[j]=1表示与偶数j匹配的前一奇数为1。初始化素数伴侣的标志位used数组为0,若used[i]=1表示偶数i已经被使用与其他奇数构成伴侣。
进入循环,在匈牙利算法中寻找增广路,若找到增广路则计数值加一。
接下来讲解匈牙利算法,代码如下:
//匈牙利算法
bool dfs(int k)
{
for(int i=0;i根据上述矩阵来讲解匈牙利算法,在匈牙利算法中首先used[G[1][1]]=used[2]=0使其置1表示偶数2已经被使用与其他奇数构成了伴侣。pre[G[1][1]]=0表示还没有与偶数2匹配的奇数,程序继续执行将pre[G[1][1]]=1表示与偶数2匹配的奇数为1。当执行到偶数行时直接跳过。当程序执行到矩阵的第5行要找与5匹配的偶数时,used[G[5][1]]=used[2]=0,程序将其置1表示偶数2已经被使用与奇数5构成了伴侣,pre[G[5][1]]=pre[2]=1发现偶数2之前与奇数1已经进行过一次匹配。然后程序进入dfs(pre[G[5][1]])=dfs(1),再重新对1寻求未匹配的偶数然后找到偶数4,发现偶数4之前与奇数3进行过匹配,则进而对奇数3再寻找未匹配的偶数,找到偶数6,发现pre[G[3][2]]=0表示还没有与偶数6匹配的奇数,则找到一个未匹配的点偶数6,进而找到一条增广路则计数值加1。
整理一下思路,当程序执行到矩阵的第5行要找与5匹配的偶数时,从未匹配点5开始经过未匹配边5-2,匹配边2-1,未匹配边1-4,匹配边4-3,未匹配边3-6,找到未匹配点6.找到一条增广路。对其所有顶点就行循环则完成了二分图的最大匹配,也解决了素数伴侣问题。
整体代码如下:
#include
#include
#include
using namespace std;
vector G[105];
int pre[105];
bool used[105];
bool dfs(int k)
{
for(int i=0;i>N)
{
for(int i=1;i<=N;++i)
{
cin>>temp;
nums[i]=temp;
}
//匹配规则
for(int i=1;i<=N;++i)
{
for(int j=i+1;j<=N;++j)
{
if(isprime[nums[i]+nums[j]])
(nums[i]&1)?G[i].push_back(j):G[j].push_back(i);//如果是奇数
}
}
memset(pre,0,sizeof(pre));
int count=0;
for(int i=1;i<=N;++i)
{
memset(used,0,sizeof(used));
if(dfs(i))
count++;
}
cout<