Codeforces Round #595 (Div. 3)改题

B2. Books Exchange (hard version)

time limit per test1 second
memory limit per test256 megabytes
inputstandard input
outputstandard output
The only difference between easy and hard versions is constraints.

There are n kids, each of them is reading a unique book. At the end of any day, the i-th kid will give his book to the pi-th kid (in case of i=pi the kid will give his book to himself). It is guaranteed that all values of pi are distinct integers from 1 to n (i.e. p is a permutation). The sequence p doesn’t change from day to day, it is fixed.

For example, if n=6 and p=[4,6,1,3,5,2] then at the end of the first day the book of the 1-st kid will belong to the 4-th kid, the 2-nd kid will belong to the 6-th kid and so on. At the end of the second day the book of the 1-st kid will belong to the 3-th kid, the 2-nd kid will belong to the 2-th kid and so on.

Your task is to determine the number of the day the book of the i-th child is returned back to him for the first time for every i from 1 to n.

Consider the following example: p=[5,1,2,4,3]. The book of the 1-st kid will be passed to the following kids:

after the 1-st day it will belong to the 5-th kid,
after the 2-nd day it will belong to the 3-rd kid,
after the 3-rd day it will belong to the 2-nd kid,
after the 4-th day it will belong to the 1-st kid.
So after the fourth day, the book of the first kid will return to its owner. The book of the fourth kid will return to him for the first time after exactly one day.

You have to answer q independent queries.

Input
The first line of the input contains one integer q (1≤q≤1000) — the number of queries. Then q queries follow.

The first line of the query contains one integer n (1≤n≤2⋅105) — the number of kids in the query. The second line of the query contains n integers p1,p2,…,pn (1≤pi≤n, all pi are distinct, i.e. p is a permutation), where pi is the kid which will get the book of the i-th kid.

It is guaranteed that ∑n≤2⋅105 (sum of n over all queries does not exceed 2⋅105).

Output
For each query, print the answer on it: n integers a1,a2,…,an, where ai is the number of the day the book of the i-th child is returned back to him for the first time in this query.

---

1. 输入
   6
   5
   1 2 3 4 5
   3
   2 3 1
   6
   4 6 2 1 5 3
   1
   1
   4
   3 4 1 2
   5
   5 1 2 4 3

---

输出
1 1 1 1 1
3 3 3
2 3 3 2 1 3
1
2 2 2 2
4 4 4 1 4

---

题意：每个人手中都有一本书，此时数组他要把手中的书传给下一个人，题目给的是每个位置的人要传给的下一个人的编号,其实就是要我们找环，并且数一下环中节点个数，本来使用并查集做的，想复杂了，直接模拟就好了

#include 
using namespace std;
const int maxn = 2e5+100;
int vis[maxn];
int ans[maxn];
int a[maxn];
stack<int>s;
int main()
{
    int q , n ,x, day;
    cin >> q;
    while(q--)
    {
        memset(a,0,sizeof(a));
        cin >> n;
        memset(vis,-1,sizeof(vis));
        memset(ans,0,sizeof(ans));
        for(int i=1;i<=n;i++)
        {
            cin >> a[i];
        }
 
        for(int i=1;i<=n;i++)
        {
            day = 0;
            if(vis[i]!=-1)continue;
            x = a[i];
            while(x!=i)
            {
                s.push(x);
                x = a[x];
            }
            s.push(x);
            day = s.size();
            while(!s.empty())
            {
 
                x = s.top();s.pop();
                ans[x] = day;
                vis[x] = 1;
            }
        }
 
        for(int i=1;i<=n;i++)
        {
            cout <<ans[i]<<" ";
        }
        cout <<endl;
    }
}

---

---

---

C2. Good Numbers (hard version)

time limit per test2 seconds
memory limit per test256 megabytes
inputstandard input
outputstandard output
The only difference between easy and hard versions is the maximum value of n.

You are given a positive integer number n. You really love good numbers so you want to find the smallest good number greater than or equal to n.

The positive integer is called good if it can be represented as a sum of distinct powers of 3 (i.e. no duplicates of powers of 3 are allowed).

For example:

30 is a good number: 30=33+31,
1 is a good number: 1=30,
12 is a good number: 12=32+31,
but 2 is not a good number: you can’t represent it as a sum of distinct powers of 3 (2=30+30),
19 is not a good number: you can’t represent it as a sum of distinct powers of 3 (for example, the representations 19=32+32+30=32+31+31+31+30 are invalid),
20 is also not a good number: you can’t represent it as a sum of distinct powers of 3 (for example, the representation 20=32+32+30+30 is invalid).
Note, that there exist other representations of 19 and 20 as sums of powers of 3 but none of them consists of distinct powers of 3.

For the given positive integer n find such smallest m (n≤m) that m is a good number.

You have to answer q independent queries.

Input
The first line of the input contains one integer q (1≤q≤500) — the number of queries. Then q queries follow.

The only line of the query contains one integer n (1≤n≤1018).

Output
For each query, print such smallest integer m (where n≤m) that m is a good number.

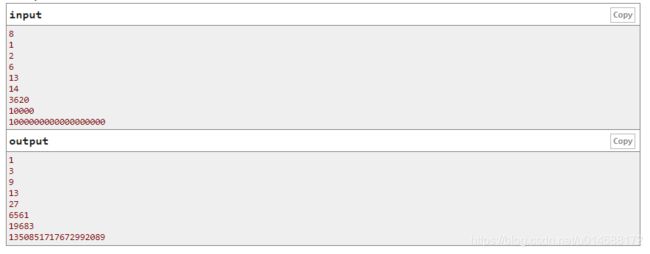
题意：将某个数转化为三进制，每一位上面不能大于1，要求我们寻找最小的比该数大的完美数，
思路：将数转化为三进制，找到最后面一位比1大的位置，将该位置前面所有的数都改为0，然后吧三进制改回十进制即可

#include 
using namespace std;
const int maxn = 100;
vector<int>v;
long long init(long long n)
{
    while(n)
    {
        v.push_back(n%3);
        n/=3;
    }
//    reverse(v.begin(),v.end());
}
long long check()
{
    long long len = v.size();
    v[len] = 0;
    long long len1 = len;
    long long pos;
    bool flag = 0;
    for(int i=0;i<len;i++)
    {
        if(v[i]==0||v[i]==1)continue;
        else
        {
            flag = 1;
            pos = i;
            v[i] = 0;
            v[i+1] += 1;
            if(i==len-1) len1 = len+1;
        }
    }
//    if(pos==0&&v[0]1)
    if(flag)
    for(int i=0;i<=pos;i++)v[i] = 0;
    return len1;
}
long long qpow(long long len)
{
    long long ans = 0,temp = 1;
    for(int i=0;i<len;i++)
    {
        if(i)temp *= 3;
        if(v[i]&1)ans +=temp;
    }
    cout << ans <<endl;
}
int main()
{
    long long t ,n;
    cin >> t;
    while(t--)
    {
//        cout << pow(3,9)<
        v.clear();
        cin >> n;
        init(n);
        long long len = check();
        qpow(len);
    }
}