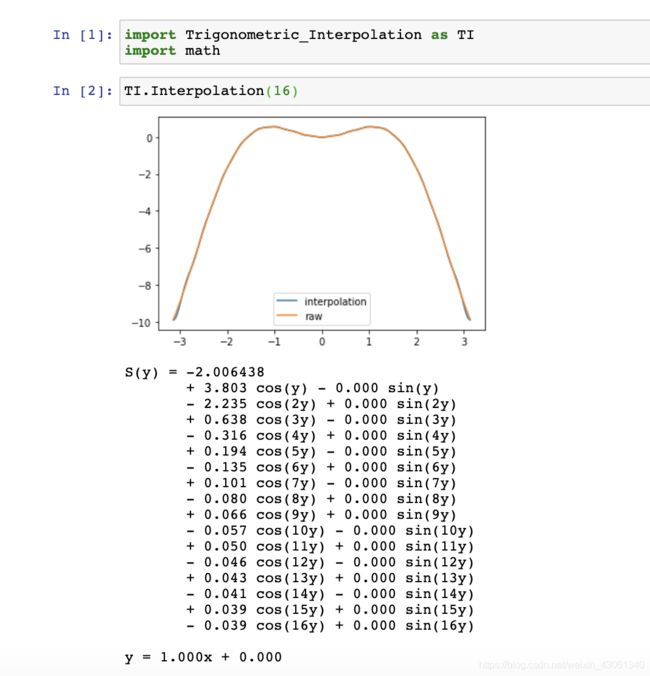
FFT实现三角插值逼近
FFT实现三角插值逼近
GoatWu 2020.03.25
一、程序摘要
此程序使用 python3.7 语言编写。引入了外部库函数 numpy 作为数学工具解方程,matplotlib 作为画图工具。由于需要多步运行,对不同的参数进行绘图,因此使用了 jupyter-notebook 作为编写工具。
由于用到的函数较多,为了安全起见,此程序将内部函数封装在了 functions.py 模块中,将接口函数封装在了 Trigonometric_Interpolation.py 模块中。在 Trigonometric_Interpolation.py 中,我们引用了 functions.py 的内部函数;在主程序中,我们只需要引入 Trigonometric_Interpolation 模块即可:import Trigonometric_Interpolation as TI。
程序实现了给定任意区间、任意函数,使用FFT确定函数的三角插值多项式。其中插值的次数并不要求严格为 2 2 2 的整数幂。
二、程序功能
1. 接口介绍
Interpolation(Interpolation_times, l = -pi, r = pi, func = f)
Interpolation_times: 给定的插值次数l: 插值区间左端点,默认为 − π -\pi −πr: 插值区间左端点,默认为 π \pi πfunc: 被插值的函数,默认为 x 3 ⋅ cos ( x ) x^3\cdot \cos(x) x3⋅cos(x)
2. 功能展示
程序实现了:
-
较工整地写出插值函数;
-
绘制出原函数与插值函数图像进行对比;
2.1. 默认情况(即作业要求)
2.1. 其他情况(书上例题)
三、源代码
1. functions.py
# 引入库函数;定义常量
import math
import numpy as np
import matplotlib.pyplot as plt
pi = math.pi
# FFT步骤1: 将复数数组引入到A1
def init_A(Interpolation_times, f, func, l, r):
point_num = 2 * Interpolation_times
A = []
interval = 2 * pi / point_num
now = -pi
for i in range (point_num):
A.append(complex(func(f, l, r, now), 0))
now += interval
return A
# FFT步骤2: 预处理单位根(各个插值节点)
def init_w(Interpolation_times):
point_num = 2 * Interpolation_times
w = []
w.append(complex(1, 0))
degree = 2 * pi / point_num
root = complex(math.cos(degree), math.sin(degree))
for i in range (1, Interpolation_times):
w.append(w[i - 1] * root)
return w
# FFT步骤4-8: DFT
def DFT(A1, w, Interpolation_times, p):
point_num = 2 * Interpolation_times
A2 = [complex(0, 0)]
A2 = A2 * point_num
for q in range(1, p + 1):
if q % 2 == 1:
for k in range(2 ** (p - q)):
for j in range(0, 2**(q-1)):
tmp1 = k * 2 ** q + j
tmp2 = k * 2 ** (q - 1) + j
tmp3 = 2 ** (p - 1)
tmp4 = 2 ** (q - 1)
A2[tmp1] = A1[tmp2] + A1[tmp2 + tmp3]
A2[tmp1 + tmp4] = (A1[tmp2] - A1[tmp2 + tmp3]) * w[k * tmp4]
else:
for k in range(2 ** (p - q)):
for j in range(0, 2**(q-1)):
tmp1 = k * 2 ** q + j
tmp2 = k * 2 ** (q - 1) + j
tmp3 = 2 ** (p - 1)
tmp4 = 2 ** (q - 1)
A1[tmp1] = A2[tmp2] + A2[tmp2 + tmp3]
A1[tmp1 + tmp4] = (A2[tmp2] - A2[tmp2 + tmp3]) * w[k * tmp4]
c = []
if p % 2 == 0:
for i in range(Interpolation_times + 1):
c.append(A1[i])
else:
for i in range(Interpolation_times + 1):
c.append(A2[i])
return c
# 将c还原至a和b
def exchange(c, Interpolation_times):
root = complex(-1, 0)
now_degree = complex(1, 0)
a = []
b = []
for i in range(Interpolation_times + 1):
ci = c[i] * now_degree
a.append(ci.real / Interpolation_times)
b.append(ci.imag / Interpolation_times)
now_degree *= root
return a, b
# FFT全过程,以上步骤的汇总
def FFT(Interpolation_times, p, f, func, l, r):
a = []
b = []
A1 = init_A(Interpolation_times, f, func, l, r)
w = init_w(Interpolation_times)
c = DFT(A1, w, Interpolation_times, p)
a, b = exchange(c, Interpolation_times)
return a, b
# 计算出三角多项式对应的点值
def ans_F(x, a, b, Interpolation_times):
res = a[0] / 2
for i in range(1, Interpolation_times + 1):
res += a[i] * math.cos(i * x) + b[i] * math.sin(i * x)
return res
# 画图函数:分别绘制原函数、拟合出的函数
def draw_pic(a, b, Interpolation_times, f, func, l, r):
x = np.arange(-pi, pi, 0.01)
y = []
yy = []
for i in range(len(x)):
y.append(ans_F(x[i], a, b, Interpolation_times))
yy.append(func(f, l, r, x[i]))
x[i] = (x[i] * (r - l)) / (2 * pi) + (l + r) / 2
fig = plt.figure()
plt.plot(x, y, label='interpolation')
plt.plot(x, yy, label='raw')
plt.legend()
plt.show()
plt.close(fig)
# 打印出拟合的结果
def judge_sign(a):
if a < 0:
return '-'
else:
return '+'
def print_trans_result(a, b, Interpolation_times, l, r):
print("S(y) = %f" % (a[0] / 2))
print(" %c %.3lf cos(y) %c %.3lf sin(y)"
% (judge_sign(a[1]), abs(a[1]), judge_sign(b[1]), abs(b[1])))
for i in range(2, Interpolation_times + 1):
print(" %c %.3lf cos(%dy) %c %.3lf sin(%dy)"
% (judge_sign(a[i]), abs(a[i]), i, judge_sign(b[i]), abs(b[i]), i))
print("")
tmp = pi * (l + r) / (r - l)
print("y = %.3lfx %c %.3lf"
% (2 * pi / (r - l), judge_sign(-tmp), abs(tmp)))
# 对于给定插值次数不是2的整数幂的处理
# 我们将插值点的个数提升至最近的2的整数幂,并对结尾进行截断
def extend(Interpolation_times):
lim = 1
p = 0
while lim < Interpolation_times:
lim *= 2
p += 1
return lim, p
2. Trigonometric_Interpolation.py
import functions as F
import math
pi = math.pi
# 内置的默认插值函数
def f(x):
return x * x * math.cos(x)
# 将函数映射到区间[-pi, pi]
# 以函数作为参数,类似Matlab的sub
def transform_f(F, l, r, x):
return F(x * (r - l) / (2 * pi) + (l + r) / 2)
def Interpolation(Interpolation_times, l = -pi, r = pi, func = f):
function = transform_f
n, p = F.extend(Interpolation_times)
a, b = F.FFT(n, p + 1, func, function, l = l, r = r)
F.draw_pic(a, b, Interpolation_times, func, function, l, r)
F.print_trans_result(a, b, Interpolation_times, l, r)
3. main.py
import Trigonometric_Interpolation as TI
import math
# 默认情况的插值
TI.Interpolation(16)
# 给定函数和区间的插值
def ff(x):
return x*x*x*x - 3*x*x*x + 2*x*x - math.tan(x*(x-2))
TI.Interpolation(4, l = 0, r = 2, func = ff)
四、实验分析
1. 变换结果的含义
注意我们要求的核心式子:
c j = ∑ k = 0 N − 1 x k ω N k j c_j=\sum_{k=0}^{N-1}x_k\omega_N^{kj} cj=k=0∑N−1xkωNkj
注意到 ω N k = ω N − k \omega_N^{k}=\omega_N^{-k} ωNk=ωN−k ,很显然,如果把 ω N \omega_N ωN 看成时域的序列,这是一个在时域卷积的式子。由傅里叶变换我们知道,时域卷积等于频域相乘。由于直接暴力卷积的复杂度是 O ( n 2 ) O(n^2) O(n2) ,在 n n n 较大时不可接受,我们考虑把序列 x k x_k xk 变换到频域。我们发现 ω N \omega_N ωN 也恰好是一系列的频域信号。
因此我们通过FFT得到的序列 c j c_j cj 就是一系列的时域信号了。由于我们的目的是利用三角函数(傅立叶级数)来逼近原函数,本身就需要的是频域信号,因此无需进行快速傅立叶逆变换(IDFT)。我们将得到的频域信号 c j c_j cj 利用欧拉公式转换成 a j a_j aj 和 b j b_j bj ,即可得到逼近函数。
抛开函数逼近这个问题,如果我们要做的是多项式乘法这种结果在时域表示的序列,我们可以将两个序列DFT,在频域相乘后得到答案的频域信号,然后通过IDFT恢复至时域。
2. 对快速傅立叶变换的理解
离散傅立叶变换巧妙的利用了单位根 ω N k \omega_N^{k} ωNk 的性质。所谓单位根,可以理解为将单位圆 N N N 等分,位于第一象限的第一个向量即是单位根。由欧拉公式,这 N N N 个向量每个与单位根做乘机可以得到下一个向量。
-
ω N k + n 2 = − ω N k \omega_N^{k+\frac{n}{2}}=-\omega_N^{k} ωNk+2n=−ωNk
理解为:一个向量旋转 180 180 180 度,得到其相反值。
-
ω N k = ω 2 N 2 k \omega_N^{k}=\omega_{2N}^{2k} ωNk=ω2N2k
利用欧拉公式可证明。
-
ω N 0 = ω N N = 1 \omega_N^{0}=\omega_N^{N}=1 ωN0=ωNN=1
易证。
利用分治的思想,我们尝试把序列分成两部分:
c j = ∑ k = 0 N / 2 − 1 x k ω N k j = ∑ k = 0 N / 2 − 1 x N / 2 + k ω N k j + ∑ k = 0 N − 1 x k ω N j ( N / 2 + k ) = ∑ k = 0 N / 2 − 1 ( x k + ( − 1 ) j x N / 2 + k ) ω N k j \begin{aligned} c_j&=\sum_{k=0}^{N/2-1}x_k\omega_N^{kj}=\sum_{k=0}^{N/2-1}x_{N/2+k}\ \omega_N^{kj}+\sum_{k=0}^{N-1}x_k\omega_N^{j(N/2+k)}\cr &=\sum_{k=0}^{N/2-1}\left(x_k+\left(-1\right)^jx_{N/2+k}\right)\omega_N^{kj} \end{aligned} cj=k=0∑N/2−1xkωNkj=k=0∑N/2−1xN/2+k ωNkj+k=0∑N−1xkωNj(N/2+k)=k=0∑N/2−1(xk+(−1)jxN/2+k)ωNkj
按照奇偶分组后可将序列分成两部分,可以再分别进行DFT:
l e t : y k = x k + x N / 2 + k , y N / 2 + k = ( x k − x N / 2 + k ) ω N k let:\ \ \ \ y_k=x_k+x_{N/2+k},\ \ y_{N/2+k}=\left(x_k-x_{N/2+k}\right)\omega_N^{k} let: yk=xk+xN/2+k, yN/2+k=(xk−xN/2+k)ωNk
c 2 j = ∑ k = 0 N / 2 − 1 x k ω N / 2 k j c 2 j + 1 = ∑ k = 0 N / 2 − 1 y N / 2 + k ω N / 2 k j \begin{aligned} c_{2j}&=\sum_{k=0}^{N/2-1}x_k\omega_{N/2}^{kj}\cr c_{2j+1}&=\sum_{k=0}^{N/2-1}y_{N/2+k}\omega_{N/2}^{kj} \end{aligned} c2jc2j+1=k=0∑N/2−1xkωN/2kj=k=0∑N/2−1yN/2+kωN/2kj
复杂度分析: T ( n ) = 2 T ( n 2 ) + n = O ( n l o g n ) T(n)=2T\left(\frac{n}{2}\right)+n=O(nlogn) T(n)=2T(2n)+n=O(nlogn) 。
3. 对快速傅立叶变换的一些感想
快速傅立叶变换具有化腐朽为神奇的魔力。现在火热的深度学习,需要大量的卷积运算来提取特征,时域暴力卷积的低效让傅立叶变换大展身手;在其基础上衍生出了许多类似的算法:数论上,类似于单位根的性质,一些具有特殊性质的质数可以利用原根进行快速数论变换(NTT);类似于其分治思想,又有了下标卷积的快速沃尔什变换(FWT)。
当然浮点误差是FFT较大的缺陷。很明显的,同样的算法下,我的拟合函数就和书上略有差别。工业上,python 和 Java 的高精度乘法均没有使用 FFT 算法,基础的运算操作即便是极为微小的差错也是不可饶恕的。但不论怎样,FFT都是一个优秀而高效的算法。