小白入门关联规则之子图模式的类Apriori方法和gSpan算法挖掘学习
关联规则之子图模式
- 关联规则之子图模式
- 文章目的
- 基本概念
- 类apriori方法
- gSpan算法
- DFS编码
- 最右扩展
- 实验研究
- 参考博客
- 参考文献
关联规则之子图模式
文章目的
- 了解子图模式在什么情况下使用
- 理解子图模式的概念和原理
- 学习子图模式的两种算法
- 研究子图模式的算法应用
基本概念
首先我们要明白这样一个事情,在这么多关联规则的方法中,我们为什么要使用子图模式。这种子图模式在什么领域应用?
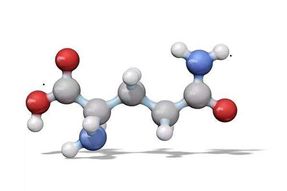
图1
由上图1我们可以看到,有顶点有边。假设这是一个蛋白质的图,图中的顶点就代表了氨基酸,图中的边代表了氨基酸与氨基酸之间的化合作用,在这种情况下,由于常用氨基酸只有20种,所以图中的顶点必定会重复。但是,如果使用的是频繁项集的表示方法,由于项在项集中最多出现一次,且无法表示出图中顶点的关系,显然就无法完整地通过频繁项集把类似于图1表示出来。所以我们需要引入一种方法来表示这样的结构关系,那就是频繁子图。
另外,可以看到子图模式的实际应用领域,如下表所示。
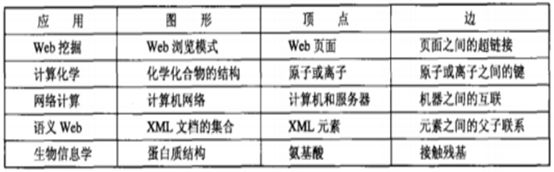
通过前面的引入,我们对子图模式有一个直观的理解。接下来就介绍一下子图模式的基本概念。
子图:图G′=(V′,E′) 是另一个图G=(V,E) 的子图,如果它的顶点集V’是V的子集,并且它的边集E’是E的子集,子图关系记做G′⊆sG
支持度:给定图的集族ς, 子图g的支持度定义为包含它的所有图所占的百分比。
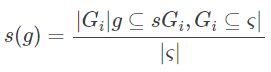
由于支持度是我们算法输入的一个参数,我们需要对支持度进一步说明该公式是什么意思,如下图2所示,g1是G1、G3、G4和G5的子图,支持度=4/5=80%。
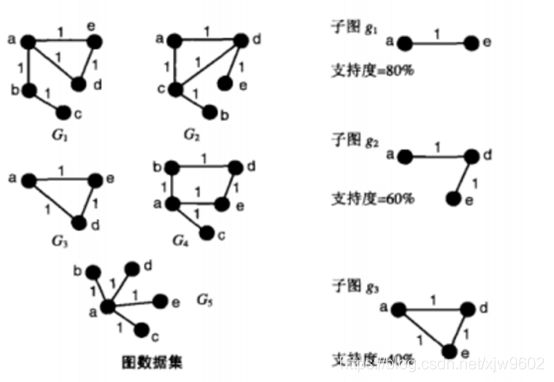
图2
到此,子图模式的基本概念,我们能够理解。接下来学习子图模式的类apriori方法和gspan算法。
类apriori方法
首先明确我们的目标是频繁子图挖掘。那么频繁子图挖掘怎么判断是频繁呢?我们来看一下概念。频繁子图挖掘 :给定集合ς和支持度阈值minsup,频繁子图挖掘的目标是找出使得所有s(g)≥minsup的子图g。
具体的步骤分为以下四步:
- 候选产生
- 候选剪枝
- 支持度计数
- 候选删除
我们来看候选产生,候选产生有两种常用方法,分别为顶点增长和边增长。顶点增长:通过添加一个新的结点到已经存在的一个频繁子图上来产生候选。可以使用邻接矩阵来表示图,每一项M(i,j)为链接vi和vj的边或者0。如下图3所示,顶点增长方法可以看作合并一对(k-1)X(k-1)的邻接矩阵,产生K x K邻接矩阵的过程。
图3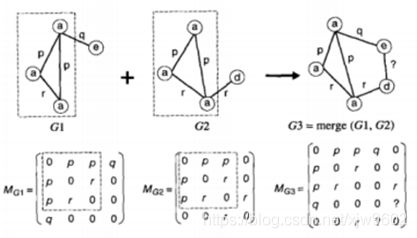
图3
在上图3中,G1 和G2都含有4个顶点和4条边。合并之后,图G3有5个顶点,但G3边的数目取决于顶点d和e是否相连。如果d和e时不相连的,则G3有5条边,并且(d,e)对应的矩阵项为0;否则,G3有6条边,并且(d,e)的矩阵项对应与新创建的边的标号。由于该边的标号未知,我们需要对(d,e)考虑所有可能的边标号,从而大大增加了候选子图的个数。
通过边增长产生候选,边增长将一个新的边插入一个已经存在的频繁子图中,与顶点增长不同,结果子图的顶点个数不一定增加,如下图4所示。
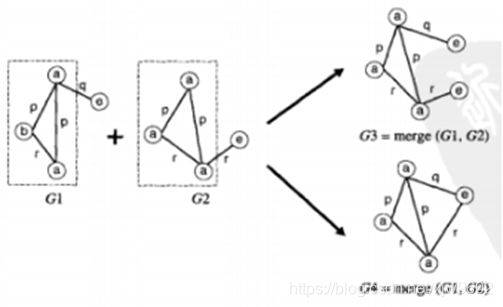
图4
由上图显示了通过边增长策略合并G1和G2得到的来给你个可能的候选子图。第一个候选子图G3多了一个顶点,而第二个候选子图G4的顶点个数与原来的图一样。
候选剪枝
产生候选k子图后,需要减去(k-1)子图非频繁的候选。候选简直可以通过如下步骤实现:相继从k子图中删除一条边,并检查对应的(k-1)子图是否连通且频繁。如果不是,则该候选k子图可以丢弃。意思是一次删除一条,总共有k个子图要检测。
为了检查(k-1)-子图是否频繁,需要将它和其他频繁(k-1)-子图匹配,判定两个图是否拓扑等价称为图同构问题。图同构是什么意思呢?即若图的顶点可以任意移动,边是弹性的,只要在不拉断的条件下,一个图可以变形为另一个图。如下图5所示,这两个图是同构的。
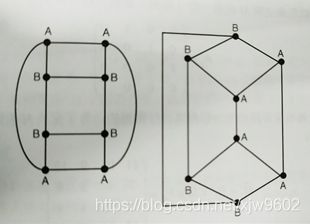
图5
此时,我们可以知道图是同构的,又由于图的表示从不同顶点开始建立的邻接矩阵是不一样的,也就是说一个图的邻接矩阵表示有很多个。我们就需要对于每个图建立一个唯一的表示。也称为规范标号。若图是同构的,则规范标号相同,通过比较规范标号来检查图同构。那么如何构造图的规范标号呢?步骤如下:
- 找出图的邻接矩阵表示,利用矩阵中基本矩阵进行行列互换
- 确定每个矩阵的串表示,由于邻接矩阵是对称的,因此只需要根据矩阵的上三角部分构造。
- 比较图的所有串表示,并选出具有最小(最大)字典序值的串,确保每个图的串表达式唯一
当我们剪枝完成之后,将剪枝后剩余的候选图进行支持度计算,将其中大于支持度阈值的候选图记为满足条件的频繁子图。下面公式为计算支持度的公式。
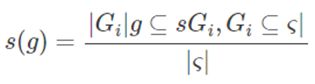
至此,类apriori方法介绍完毕,但是在每一层频繁子图的挖掘过程中,Apriori算法都会产生大量的非频繁的候选子图。然后对候选的频繁子图执行支持度计数。对于所有频繁的候选子图,还需要进行图的同构测试,以减除重复的频繁候选子图。因为图的同构测试是一种NP完全问题,所以对于大规模的频繁子图进行图的同构测试是一个开销很大的过程,甚至是不可能完成的任务。因此,大量生成的候选子图和图的同构测试的巨大开销是Apriori类方法的性能瓶颈。
gSpan算法
所以,接下来介绍另外一种算法,gspan算法。gSpan算法通过执行最右扩展的策略减少了重复的产生,同时也保证了搜索结果的完备性。gSpan算法设计出一种新式的图的规范标号,将图的同构测试与重复图的检测结合到一块,避免了在已经获得的频繁子图集合中搜索重复图。
DFS编码
为了遍历图,gSpan算法采用深度优先搜索。初始,随机选择一个起始顶点,并且对图中访问过的顶点做标记。被访问过的顶点集合反复扩展,直到建立一个完全的深度优先搜索 (DFS) 树。这种新式的规范标号就是dfs编码。如下图所示,对于每个加下标的图, 可以将其转换成边序列。
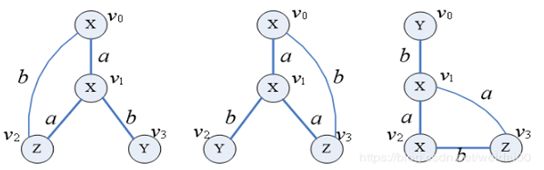
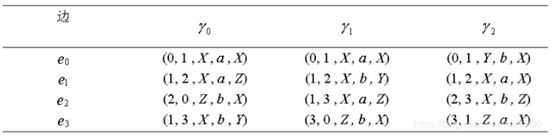
最右扩展
给定图G 和G 的DFS树T ,一条新边e 可以添加到最右节点和最右路径上另一个节点之间(后向扩展);或者可以引进一个新的节点并且连接到最右路径上的节点(前向扩展)。由于这两种扩展都发生在最右路径上,因此称为最右扩展。
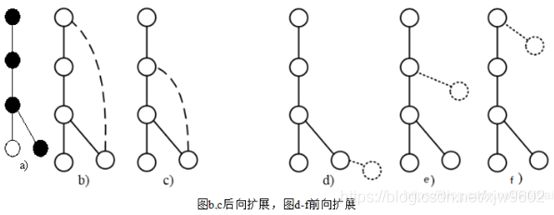
如上图所示,图b是扩展时候第一优先级,如果第一优先级的子图是不符合规则的或者在所有子图中是不频繁的,那么进入第二优先级c。途中从b到f分别是优先级从第一到第五。
因此,了解基本概念的dfs编码和最右扩展后,下面以一个具体例子进行说明。
首先,当我们拿到这样的图输入。可以看到
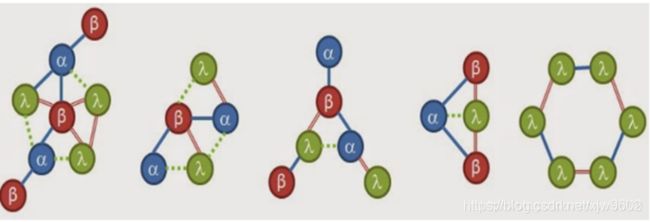
图里共有有7个alpha(α)顶点,8个beta(β)顶点和14个lambda(λ)顶点。有15个边缘为纯蓝色,13个为双红色,8个为绿色点缀。然后将最高计数的顶点和边开始降序排列标号。
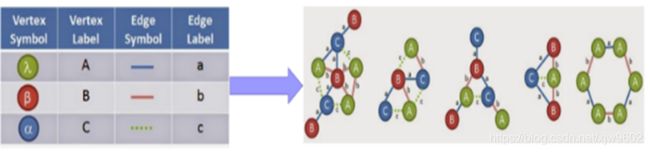
标号好后,查看各个边(例如:A,b,A),看是否满足最小支持阈值。比如,(B,a,C)可以在四个图中找到,所以支持数量为4,同理查找所有边。
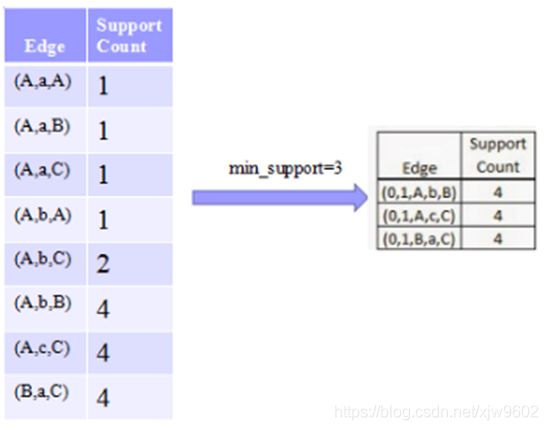
查找结果如上图所示,假设最小支持度为3,最后能够得到的边为(0,1,A,b,B)、(0,1,A,c,C)、(0,1,B,a,C),这三条边为频繁子图开始,以其中一条边开始扩展,后面在频繁子图出现的边也必须是这三条边中的一条,因为这些才是频繁的。

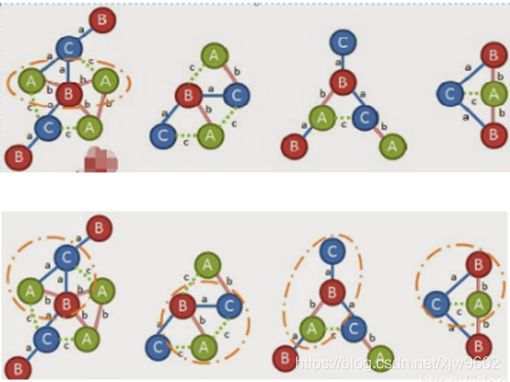
首先从(0,1,A,b,B)开始扩展,遇到(1,2B,aC)支持度为4,说明可以从这个边开始继续扩展,下面并列的(0,2A,c,C)待定。


接下来又找到了(2,0,C,c,A)作为扩展边,支持度为4.然后继续按照最有扩展规则进行扩展。

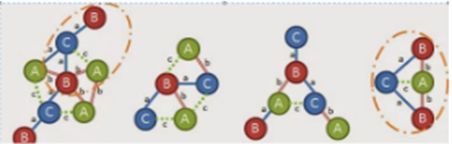
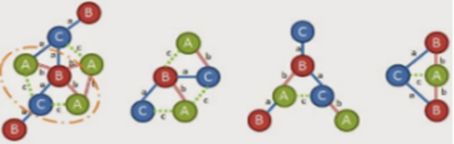
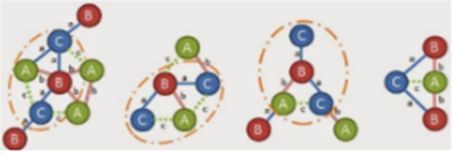
此时,找到(1,3,B,a,C)符合规则,可以得到到现在为止,我们的扩展的图是;
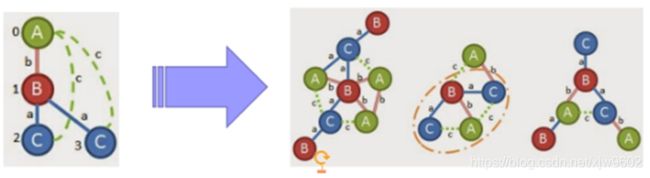
接下来,基于优先级规则,将顶点3链接到顶点0,如上图所示,仅存在一个,所以进入下一个优先级,但是顶点3和顶点1已经链接,因此需要添加顶点。
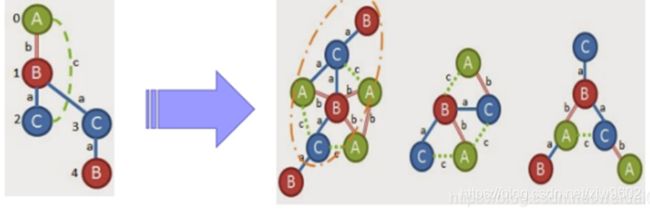
此时添加(C,a,B),但只存在一个。又尝试添加 (C,c,A),但在图中找不到。所以需要从根‘A’增长,可以使用(A,b,B)或(A,c,C).
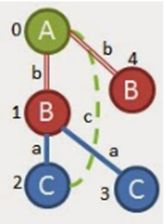
从添加(A,b,B)开始,得到如右图所示子图,但在原图集中找不到。
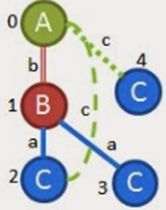
从添加(A,c,C)开始,得到如右图所示子图,但在原图集中找不到。
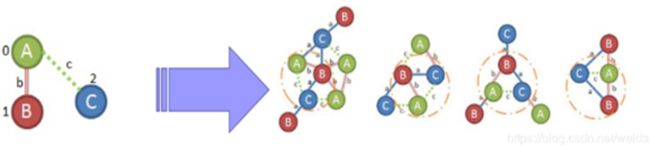
此时,回到最近一个待定状态(1,3,B,b,A),其support<3,继续回到(0,3,A,c,C)support<3,继续回到上一个待定状态(0,2,A,c,C),可得图上图所示。
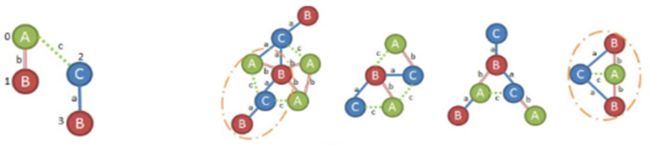
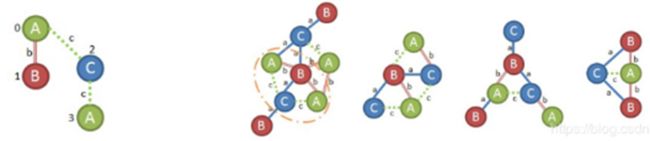
从C节点扩展,我们的两个选项是(2,3,C,a,B)和(2,3,C,c,A)分别添加后,如上图所示。
此时,第一条边(0,1,A,b,B)扩展结束,接下来同理扩展第二条边(0,1,A,c,C),并且在原图中删除(A,b,B)边,原图变为:
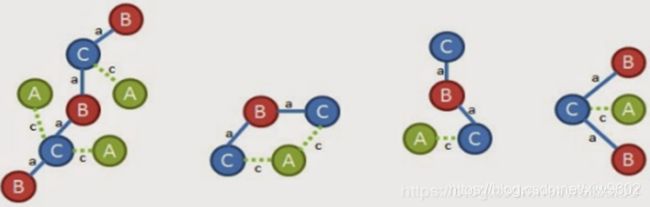
从上图中继续扩展(0,1,A,c,C),最终通过三条边的扩展可以得到频繁子图:
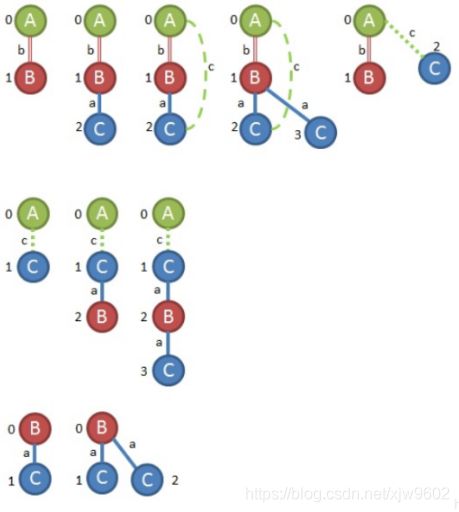
至此,gspan算法挖掘结束。接下来探索一下实验研究。
实验研究
首先我们先来看一下gspan算法的输入和输出。
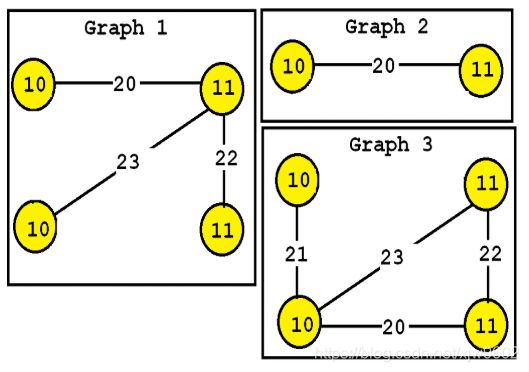
当我们有上面图集,首先需要将其抽象成数字进行输入。如下所示,
T # 0 表示这是图形的第一行,文件中第0个图
V 0 10 表示当前图形的第0个顶点,带有标签10
E 0 1 20 表示第0个顶点和第1个顶点,边的标签是20

然后经过算法的运算执行,可以得到输出为:

T # 0 * 3 表示文件中第0个图,支持度为3
V 0 10 表示第0个顶点,标签为10
x 0 1 2 表示在包含当前子图的所有图的标签。
如上所示,不同频繁子图是不同的氨基酸结构, 氨基酸结构(T # 0 * 3)是促使长高蛋白质,氨基酸结构(T # 1 * 3)是促使长帅蛋白质。原图即不同的蛋白质,不同的氨基酸结构会影响蛋白质的功能.那么我们是否可以找到又高又帅的蛋白质呢?
因此,我们拿到频繁子图和对应的图集,也就是拿到氨基酸结构和对应的蛋白质。我们是否可以从这些筛选出来的蛋白质中再进行挖掘,运用apriori方法,从这些蛋白质中找到又高又帅的蛋白质。
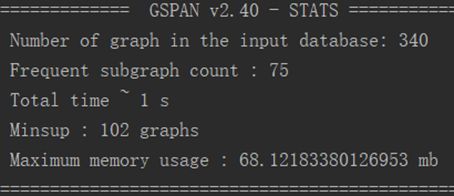
这是我们的运行结果,340个图的真实数据集,设置支持度为30%,即具有该频繁子图的蛋白质占所有蛋白质的30%,输出75个频繁子图。
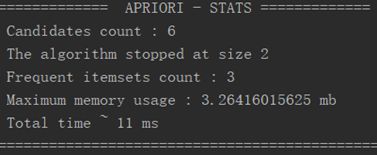
然后75个频繁子图对应的原图序号,就是apriori算法的输入(这里设定阈值为90%)。最终找到某些蛋白质中包含的氨基酸结构是最多的,也就是包含频繁子图是最多的。那么这个就是我们所要研究的蛋白质。然后把这个蛋白质的所有的氨基酸结构给画出来。

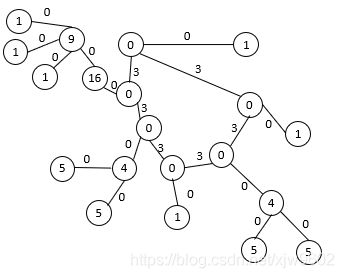
最终得到的结果如上图所示,12号、23号和38号蛋白质具备的频繁子图最多,可以理解为这就是我们要找的又高又帅的蛋白质。该蛋白质如下图所示:
参考博客
https://blog.csdn.net/weidai00/article/details/85245217
https://www.cnblogs.com/wbwang/p/7535307.html#_Toc482375353
http://www.philippe-fournier-viger.com/spmf/index.php?link=FAQ.php
http://blog.sina.com.cn/s/blog_6fb7db430100ve2w.html
https://www.cnblogs.com/zhang293/p/9427988.html
参考文献
[1]宋美娜,金远平.一个基于DFS编码的图形匹配算法[J].计算机与数字工程,2009,37(09):72-75.
[2]郭玉林,刘勇.频繁子图挖掘算法gSpan的设计与实现[J].智能计算机与应用,2011,1(05):55-57.
[3]吴卫江. Apriori算法思想在频繁子图挖掘中应用的研究[C]. 中国仪器仪表学会.第六届全国信息获取与处理学术会议论文集(2).中国仪器仪表学会:《仪器仪表学报》杂志社,2008:172-175.
[4]王艳辉,吴斌,王柏.频繁子图挖掘算法综述[J].计算机科学,2005(10):193-196+250.
[5]鲁慧民,冯博琴,宋擒豹.频繁子图挖掘研究综述[J].微电子学与计算机,2009,26(03):156-161.
[6]gSpan: Graph-Based Substructure Pattern Mining(原作者文章)