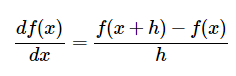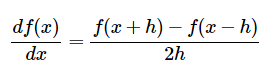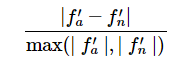斯坦福大学深度学习公开课cs231n学习笔记（8）神经网络学习过程中的检查事项和参数调优

在这节课中，主要讲述了神经网络的检查事项（例如梯度检查，合理性检查和学习过程中对损失函数、权重、每层的激活函数与梯度分布等的检查等）和神经网络的参数调优实现方法（例如：随机梯度下降方法，动量方法，学习率退火方法等等）

-----------第一部分：检查事项----------

梯度检查：

课中提出当使用有限差值来近似计算数值梯度的时候，下面的公式方法是不可行的：

          （1）

而在实际中常使用下面的中心化梯度计算公式：

  （2）

公式2的结果要比公式1更准确，公式1的误差近似为O(h)，第二个公式的误差近似为O(h^2)，

另外，在进行误差比较时，应该使用下面的相对误差比较法：

                      （3）

公式3比较误差时是计算的两者的差值占两个梯度绝对值较大值（分母取的是两个梯度绝对值的最大值）的比例，分母也可以是两个梯度绝对值的和。这样做可以防止当其中一个梯度等于0时，分母为0的情况（这种情况在ReLU中经常发生），所以还需要注意当两个梯度都为零时并且通过了梯度检查的情况。老师给出了在实践中的几种情形：

• 相对误差>1e-2，通常意味着梯度可能出错了。
• 1e-2>相对误差>1e-4，这个结果也不是很好。
  
• 相对误差<1e-4，这个结果对于含有不可导点的目标函数是可以的；但如果目标函数不存在kink（例如使用tanh和softmax），那么相对误差还是有点大。
  
• 相对误差<1e-7，或者更小，表示这是好的结果。
  

在多层神经网络中，误差时逐层累积的。对于一个可微分函数，如果误差为1e-2，通常就是梯度计算出错了。

另外，梯度检查时所用的数值精度也会影响到结果，例如，可能出现使用单精度数的相对误差为1e-2，但使用双精度数时的相对误差为1e-8的情况。 还需要注意保持浮点数的有效范围，在论文《What Every Computer Scientist Should Konw About Floating-Point Artthmetic》描述了多种可能因为浮点数值计算导致的错误。老师建议将原始的解析梯度和数值梯度数据打印出来，以确保用来比较的数值不要太小（通常绝对值小于1e-10是很坏的情况）。但是如果出现确实过小的情形，可以借助一个常数将损失函数的数值范围暂时扩展到一个更“好”的范围，使得浮点数变得更加密集；比较理想的数值范围是在1.0的数量级上，即浮点数指数为0。

还有一种情况是：目标函数存在不可导点（kinks）。

不可导点是指目标函数不存在导数的部分，ReLU、SVM损失函数、Maxout神经元等都存在kinks点。以ReLU函数为例，当x=0时，函数不可导，即是函数的一个kinks点，下图1是ReLU的函数曲线：

  图1

在x=e-6处，理论梯度应该是0，但当使用上面公式（2）求梯度时，如果h>e-6，求出的梯度结果并不为0，因为 f(x+h) 越过了不可导点。而在实际应用中，上述情况是很常见。例如，用CIFAR-10训练的SVM中，样本数为50000个，每个样本产生9个 max(0,x) 式子，所以共有 450,000个式子，所以遇到很多的不可导点是正常现象。

针对上面的情形，课中给出的建议是：

（1）使用少量的数据点。因为含有不可导点损失函数的数据点越少，出现的不可导点就越少，在计算有限差值近似时越过不可导点的概率就越小；并且这还可以使得检查过程变得高效。

（2）谨慎设置步长 h 。步长值并不是越小越好，当h过小时，可能会遇到上面说的数值精度问题。如果梯度检查无法进行，可以尝试将 h 调到1e-4或者1e-6。

（3）需要注意梯度检查的时机。最好让神经网络学习一小段时间，等到损失函数开始下降的以后再进行梯度检查。因为如果从一开始就进行梯度检查，此时梯度可能正处于不正常的边界。

另外，梯度检查还需要注意的三点有：

（1）计算数据损失时注意正则化损失的影响，不要让正则化损失掩盖数据损失。

由于损失函数包括数据损失和正则化损失两部分，所以可能存在正则化损失吞没数据损失的风险。建议做法是：先关掉正则化部分，而是对数据损失做单独检查，然后再对正则化损失做单独检查。

对正则化做单独检查的方法有：1. 修改代码，去掉其中数据损失的部分； 2.提高正则化强度，确认其效果在梯度检查中能否忽略。

（2）注意随机失活和数据扩张的不确定影响。

这可能给计算梯度结果带来不确定的误差影响。如果关闭这些操作，则无法对它们进行梯度检查（例如随机失活的反向传播可能存在错误），所以更好的解决方法是在计算 f(x+h) 和 f(x-h) 前强制增加一个特定的随机种子，在计算解析梯度时也采取这个方法。

（3）检查少量的维度。

在实际应用中，神经网络可能有上百万的参数，在这种情况下只能检查部分维度。但需要注意的是，选取的参数应该从所有不同的参数中选取部分检查，避免出现从参数向量中随机选取出的参数可能只是偏置参数的情况。

进行学习之前的合理性检查技巧：

参数调优的过程是费时费力的，所以在开始之前，下面的技巧是很有必要的：

（1）原文中“Look for correct loss at chance performance”，这里的chance performance指的是不是统计概率中的得分的意思（我不确定，如果有清楚的还望告知！）。 当使用小参数初始化时，确保得到的损失值与期望的损失值是一样的。最好的方式是单独对数据损失进行检查（正则化强度置零）。

（2）当增大正则化强度时，查看损失值是否跟着变大。

（3）在整个数据集进行训练之前，先在一个很小的数据集上进行训练（比如20个数据），并设置正则化强度为0，确保此时的损失值为0。只有这个检查通过，整个数据集的训练才有意义。

学习过程中的检查：

在神经网络训练过程中，有许多有用的参数（例如损失函数值，验证集和训练集的准确率，权重的更新比例等）需要监控，这些参数对于不同超参数的设置和调优具有指导意义。

（1）损失函数值

图2

上图2中，x轴表示周期。左面是不同学习率对应的损失函数值曲线；右图是一个典型的损失函数值随时间的变化曲线。从左图中，我们发现，学习率设置过高时，损失值并不单调了，而红色曲线对应的是较好的学习率。

另外，损失函数值的震荡程度还与批尺寸（batch size）有关：当批尺寸为1时，震荡相对会比较大；当批尺寸是整个数据集时，震荡会比较小，因为每个梯度的更新都在单调地优化损失函数（学习率过高除外）。

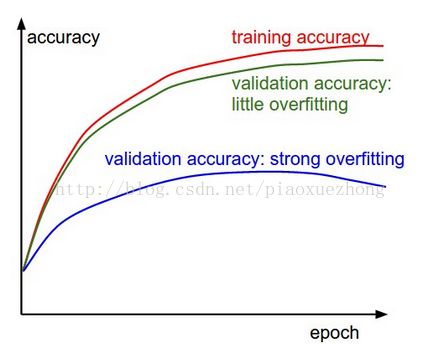
（2）训练集和验证集的准确率

   图3

上图3中，蓝色的验证集曲线表明相比于训练集/验证集的准确率低了很多，两者中间的缝隙程度也能模型过拟合的程度。此时应该增大正则化强度（更大的权重惩罚，更多的随机失活等）或者收集更多的数据。 如果遇到验证集曲线和训练集曲线近乎重合的情况，说明模型容量不够大，此时应该通过增加参数的数量使得模型容量更大些。

（3）权重的更新比例

这个之前课中也提过，这个参数指的是每次训练后有更新的权重占所有权重的比例。经验性的结论是这个比例应该在1e-3左右，如果小于此值，表明学习率可能设置的过小；如果大于此值，表明学习率可能设置的过大。

（4）课中还给出了几种判别学习过程是否出现问题的方法

• 输出网络中所有层的激活数据和梯度分布的柱状图。例如，使用tanh的神经元的激活数据的值，应该分布在整个[-1,1]区间内，但如果出现神经元的输出全部是0，或者集中在-1和1上，那么就表明有问题了。
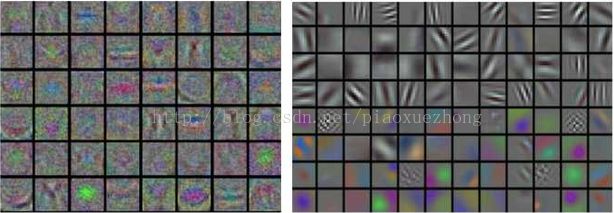
• 如果数据是图像像素数据，可以把第一层特征可视化。
  

  图4

上图是将将神经网络的第一层权重可视化的例子。左边的特征充满了噪音，表明网络可能出现了以下问题：网络不收敛，学习率设置不恰当，正则化惩罚的权重过低等。右边的特征比较平滑，干净而且种类多，表明训练过程良好。

-----------第二部分：参数调优----------

参数更新：

优化算法是通过改善训练方式，来最小化(或最大化)损失函数的过程。优化算法分为两大类：
1. 一阶优化算法。为了计算多变量函数的导数，会用梯度取代导数，使用偏导数来计算梯度。

2. 二阶优化算法。 二阶优化算法使用二阶导数(也叫Hessian方法)优化损失函数。课中也提及了其迭代公式，但是由于其计算成本比较高，所以应用的并不广泛，不加说明了。

当可以使用反向传播计算解析梯度后，梯度能被用来进行更新参数的过程。课中提及了几种网络优化算法：梯度下降法，动量更新法，学习率退火法等。

（1）梯度下降法。 参数更新最简单的方式是沿着梯度负方向改变参数。假设参数向量为x ，其梯度为dx，更新形式为：

x += - learning_rate * dx

其中，learning_rate是之前说的学习率。
注：批量梯度下降在计算损失函数的梯度时，是遍历数据集中的每一个样本，如果在每一次迭代中都进行梯度下降是非常低效的，因为算法的每次迭代仅以很小的步进来提升损失函数。为了解决这个问题，可以使用小批量（Mini-batch）梯度下降算法，该算法在数据集的一个小批量上近似计算梯度，然后使用这个梯度去更新权值。比如卷积神经网络，每次在训练集中选择包含256个样本的一批数据，然后使用这批数据计算梯度，完成参数更新，代码附在下面。用来估计梯度的 batch 大小是可以选择的一个超参数，当它等于 1 时，即为随机梯度下降（SGD），大多数深度学习框架都会选择随机梯度下降的 batch 大小。

#批量梯度下降的实现：
while True:
  weights_grad = evaluate_gradient(loss_fun, data, weights)
  weights += - step_size * weights_grad # perform parameter update

#小批量梯度下降的实现
while True:
  data_batch = sample_training_data(data, 256) # sample 256 examples
  weights_grad = evaluate_gradient(loss_fun, data_batch, weights)
  weights += - step_size * weights_grad # perform parameter update

#随机梯度下降的实现
while True:
  data_batch = sample_training_data(data, 1) # use a single example
  weights_grad = evaluate_gradient(loss_fun, data_batch, weights)
  weights += - step_size * weights_grad # perform parameter update

使用梯度下降的挑战：
1. 很难选择合适的学习率。学习率太小会导致网络收敛过于缓慢，而学习率太大可能会影响收敛，并导致损失函数在最小值上波动，甚至出现梯度发散。
2. 相同的学习率并不适用于所有的参数更新。尤其是训练集数据很稀疏，并且特征频率非常不同的时候；对于很少出现的特征，应使用更大的更新率。
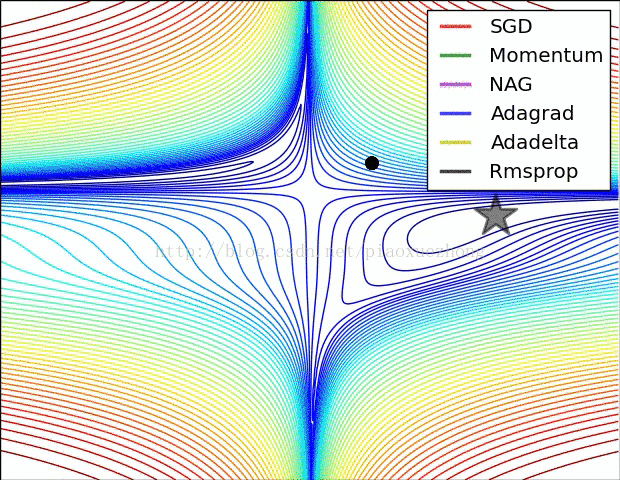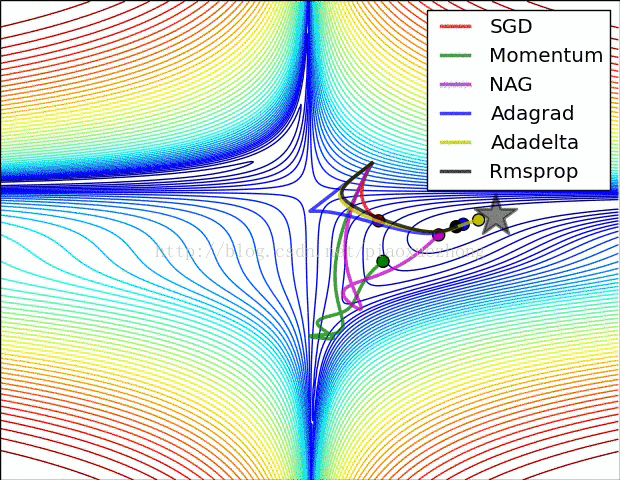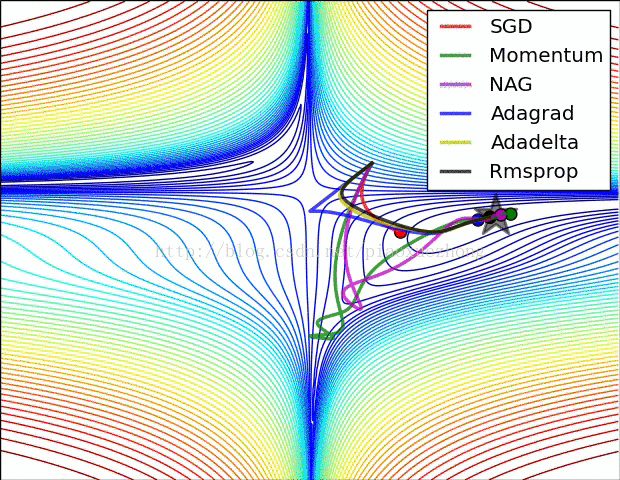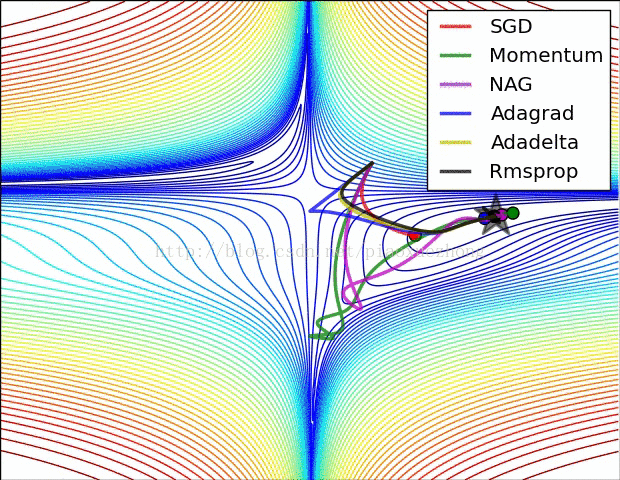
3. 在神经网络中，最小化非凸误差函数的一大挑战是避免陷于局部最小值中。实际问题中这并非源于局部极小值，而是来自鞍点，即在一个维度向上倾斜但在另一维度向下倾斜的点。鞍点通常被相同误差值的平面包围，这使得SGD算法很难脱离出来，因为梯度在所有维度上接近于零。

（2）动量更新法。动量法或说具有动量的 SGD 有助于加速向量向着正确的梯度方向下降，加快收敛速度。

SGD方法中的高方差振荡会使得网络震荡，动量（Momentum）更新方法可以通过优化相关方向的训练和弱化无关方向的振荡，来加速SGD训练过程。动量更新有两种定义方法：一种是吴恩达提出的：定义一个动量，即是梯度的移动平均值。然后用它来更新网络的权重，公式如下：

式中 L 是损失函数，α 是学习率，β为动量项，一般取值0.9。另一种表达动量更新的方式是：

# Momentum update
v = mu * v - learning_rate * dx # integrate velocity，mu即上面的动量项
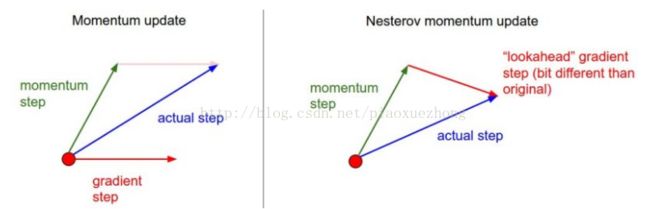
x += v # integrate position

Nesterov动量：当参数向量位于位置 x 时，由上面的代码可知，动量部分会通过 mu * v 稍微改变参数向量。可以将未来的近似位置x + mu * v 看做是“向前看”，并计算 x + mu * v处的梯度。视图如下：

实现如下：

x_ahead = x + mu * v
# evaluate dx_ahead (the gradient at x_ahead instead of at x)
v = mu * v - learning_rate * dx_ahead
x += v

（3）学习率退火算法

训练深度网络过程中，让学习率随着时间减弱是一种有效地方法。如果学习率很高，系统的动能就很大，参数向量跳动的就回厉害，不能够稳定到损失函数更深更窄的区域。通常，学习率退火有3种方式：

1. 随步数衰减：每进行几个周期就根据一些因素降低学习率。典型的值是每过5个周期就将学习率减少一半，或者每20个周期减少到之前的0.1。这些数值的设定是严重依赖具体问题和模型的选择的。在实践中可能看见这么一种经验做法：使用一个固定的学习率来进行训练的同时观察验证集错误率，每当验证集错误率停止下降，就乘以一个常数（比如0.5）来降低学习率。
2. 指数衰减。数学公式是，其中t是迭代次数（也可以使用周期作为单位）。
3. 1/t衰减。数学公式是。

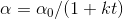单参数自适应学习率方法

前面方法中的学习率是一种全局操作，并且对所有的参数都是使用同样的学习率。学习率调参是很耗费资源的过程，下面是几种自适应学习率调参的方法。

（1）Adagrad 是由Duchi等提出的自适应学习率算法。

# Assume the gradient dx and parameter vector x
cache += dx**2
x += - learning_rate * dx / (np.sqrt(cache) + eps)

其中，变量  cache 的尺寸和梯度矩阵的尺寸是相同的，它跟踪每个参数的梯度平方和。由于， cache 放在分母位置，所以在更新参数  x 时，高梯度值的权重的学习率会被减弱，而低梯度值的权重的学习率会被增强。 eps 用于平滑（一般设为1e-4到1e-8），可以防止出现除数为0的情况。 Adagrad的缺点是，在深度学习中单调的学习率通常过于激进并且过早地停止学习。
（2） RMSprop，该方法并未发表，出自于Geoff Hinton的Coursera课程中的第六节课的第29页PPT。该方法是对Adagrad方法的改进，它 使用梯度平方的滑动平均方式使得不像Adagrad那样激进。

cache = decay_rate * cache + (1 - decay_rate) * dx**2
x += - learning_rate * dx / (np.sqrt(cache) + eps)

其中， decay_rate 是一个超参数，常用的值为[0.9,0.99,0.999]中的一个。与 Adagrad不同的是，学习率不会单调变小。

（3）Adam，Adam看起来像是RMSProp的动量版。

m = beta1*m + (1-beta1)*dx
v = beta2*v + (1-beta2)*(dx**2)
x += - learning_rate * m / (np.sqrt(v) + eps)

在引述论文中，推荐的参数值为：eps=1e-8, beta1=0.9, beta2=0.999。由于  m,v 两个矩阵初始为0，所以完整的 Adam算法还包含了偏置（bias）的矫正方法。一般， Adam比 RMSProp要好，老师推荐的更新方法是 SGD+Nesterov动量方法，或 Adam方法。

   图1   图2

图1是一个损失函数的等高线图，显示了不同最优化算法的直观效果，其中基于动量的方法出现了折返的情况。图2展示了一个马鞍状的最优化地形，其中，SGD很难突破对称性，一直卡在顶部；RMSProp等方法能够朝着马鞍方向继续前进，虽然该方向梯度小，但是由于 RMSProp方法中的分母项的存在，可以提高在该方向的学习率。

最后，附几篇拓展文章：

• Leon Bottou的《SGD要点和技巧》
• Yann LeCun的《Efficient BackProp》
• Yoshua Bengio的《Practical Recommendations for Gradient-Based Training of Deep Architectures》

参考：

http://cs231n.github.io/neural-networks-3/

https://zhuanlan.zhihu.com/p/21741716?refer=intelligentunit

https://zhuanlan.zhihu.com/p/21798784?refer=intelligentunit

http://blog.csdn.net/u012526120/article/details/49183279

https://zhuanlan.zhihu.com/p/27449596?utm_source=weibo&utm_medium=social