简单的并差集算法实例
算法学习移步:http://blog.csdn.net/dm_vincent/article/details/7655764
模板
int fa[N];
void init(int n) {
for (int i = 0; i <= n; i++)
fa[i] = i;
}
}
void unin(int u, int v) {
int fau = find(u);
int fav = find(v);
if (fau == fav) return;
fa[fav] = fau;
}
int find(int u) {
if (fa[u] != u) {
fa[u] = find(fa[u]);
}
return fa[u];
}下面是杭电的几道并差集算法例题。
HDU1232
某省调查城镇交通状况,得到现有城镇道路统计表,表中列出了每条道路直接连通的城镇。省政府“畅通工程”的目标是使全省任何两个城镇间都可以实现交通(但不一定有直接的道路相连,只要互相间接通过道路可达即可)。问最少还需要建设多少条道路?
输入:测试输入包含若干测试用例。每个测试用例的第1行给出两个正整数,分别是城镇数目N ( < 1000 )和道路数目M;随后的M行对应M条道路,每行给出一对正整数,分别是该条道路直接连通的两个城镇的编号。为简单起见,城镇从1到N编号。
注意:两个城市之间可以有多条道路相通,也就是说
3 3
1 2
1 2
2 1
这种输入也是合法的
当N为0时,输入结束,该用例不被处理。输出:对每个测试用例,在1行里输出最少还需要建设的道路数目。
代码:
#include0;
}
int find(int a){
while(a!=id[a])
a=id[a];
return a;
}
void merge(int a,int b){
int pa=find(a);
int pb=find(b);
if(pa!=pb)
id[pa]=pb;
}
int main(){
int n,m;
freopen("1.txt","r",stdin);
while(cin>>n>>m&&n){
init();
int a,b;
for(int i=0;icin>>a>>b;
merge(a,b);
}
int s=0;
for(int i=1;i<=n;i++){
if(find(i)==i)
s++;
}
cout<1< HDU1272
上次Gardon的迷宫城堡小希玩了很久(见Problem B),现在她也想设计一个迷宫让Gardon来走。但是她设计迷宫的思路不一样,首先她认为所有的通道都应该是双向连通的,就是说如果有一个通道连通了房间A和B,那么既可以通过它从房间A走到房间B,也可以通过它从房间B走到房间A,为了提高难度,小希希望任意两个房间有且仅有一条路径可以相通(除非走了回头路)。小希现在把她的设计图给你,让你帮忙判断她的设计图是否符合她的设计思路。比如下面的例子,前两个是符合条件的,但是最后一个却有两种方法从5到达8。
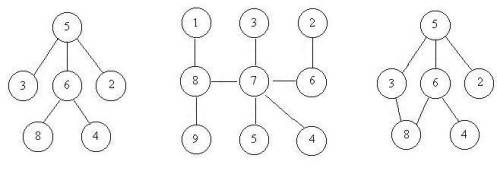
输入:输入包含多组数据,每组数据是一个以0 0结尾的整数对列表,表示了一条通道连接的两个房间的编号。房间的编号至少为1,且不超过100000。每两组数据之间有一个空行。
整个文件以两个-1结尾。
输出:对于输入的每一组数据,输出仅包括一行。如果该迷宫符合小希的思路,那么输出”Yes”,否则输出”No”。
代码
#include0;
}
int find(int a){
while(a!=fa[a])
a=fa[a];
return a;
}
void merge(int a,int b){
int pa=find(a);
int pb=find(b);
if(pa!=pb)
fa[pa]=pb;
}
int main(){
int n,m;
int flag=0;
int sum=0;
freopen("1.txt","r",stdin);
init();
while(cin>>n>>m,n!=-1&&m!=-1){
if(n==0&&m==0){
if(flag)
cout<<"No"<else{
for(int i=1;iif(vis[i]&&fa[i]==i){
sum++;
}
}
if(sum>1)
cout<<"No"<else
cout<<"Yes"<0;
sum=0;
continue;
}
vis[n]=vis[m]=1;
if(find(n)==find(m))
flag=1;
merge(n,m);
}
} HDU1269
为了训练小希的方向感,Gardon建立了一座大城堡,里面有N个房间(N<=10000)和M条通道(M<=100000),每个通道都是单向的,就是说若称某通道连通了A房间和B房间,只说明可以通过这个通道由A房间到达B房间,但并不说明通过它可以由B房间到达A房间。Gardon需要请你写个程序确认一下是否任意两个房间都是相互连通的,即:对于任意的i和j,至少存在一条路径可以从房间i到房间j,也存在一条路径可以从房间j到房间i。
输入:输入包含多组数据,输入的第一行有两个数:N和M,接下来的M行每行有两个数a和b,表示了一条通道可以从A房间来到B房间。文件最后以两个0结束。
输出:对于输入的每组数据,如果任意两个房间都是相互连接的,输出”Yes”,否则输出”No”。
代码
#includeelse
cout<<"No"< HDU1213
Today is Ignatius’ birthday. He invites a lot of friends. Now it’s dinner time. Ignatius wants to know how many tables he needs at least. You have to notice that not all the friends know each other, and all the friends do not want to stay with strangers.
One important rule for this problem is that if I tell you A knows B, and B knows C, that means A, B, C know each other, so they can stay in one table.
For example: If I tell you A knows B, B knows C, and D knows E, so A, B, C can stay in one table, and D, E have to stay in the other one. So Ignatius needs 2 tables at least.
输入:The input starts with an integer T(1<=T<=25) which indicate the number of test cases. Then T test cases follow. Each test case starts with two integers N and M(1<=N,M<=1000). N indicates the number of friends, the friends are marked from 1 to N. Then M lines follow. Each line consists of two integers A and B(A!=B), that means friend A and friend B know each other. There will be a blank line between two cases.
输出:For each test case, just output how many tables Ignatius needs at least. Do NOT print any blanks.
代码
#include