第15天:NLP——语言模型(上)
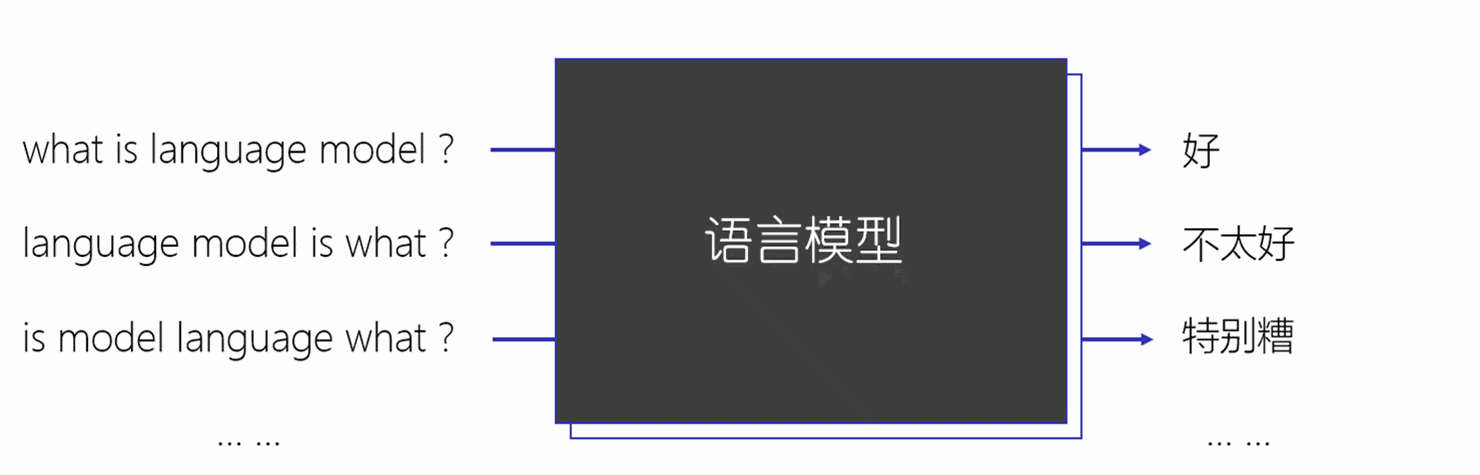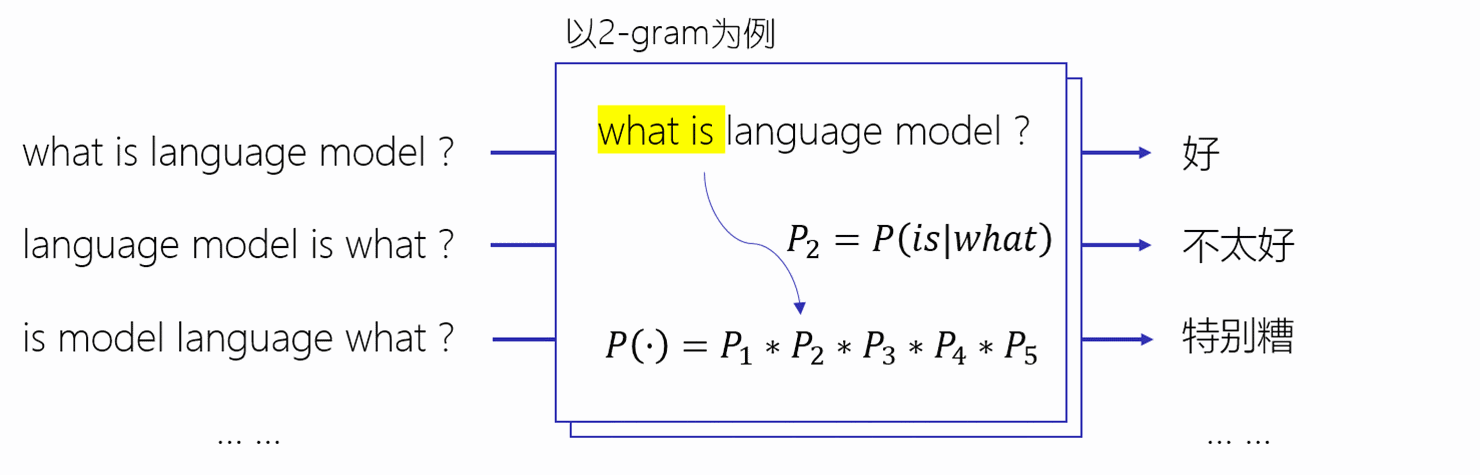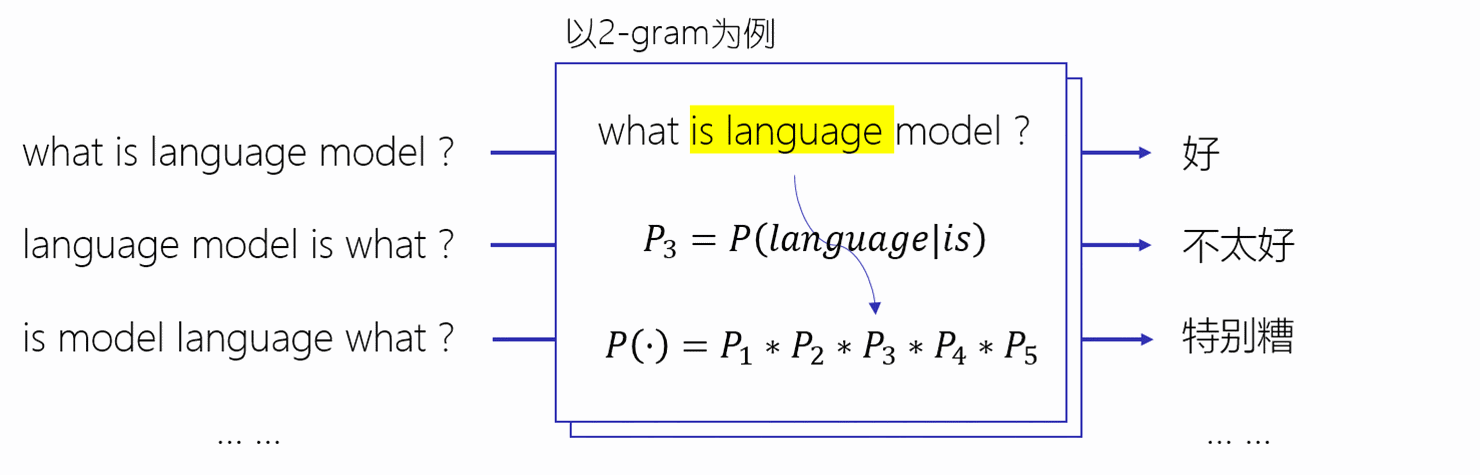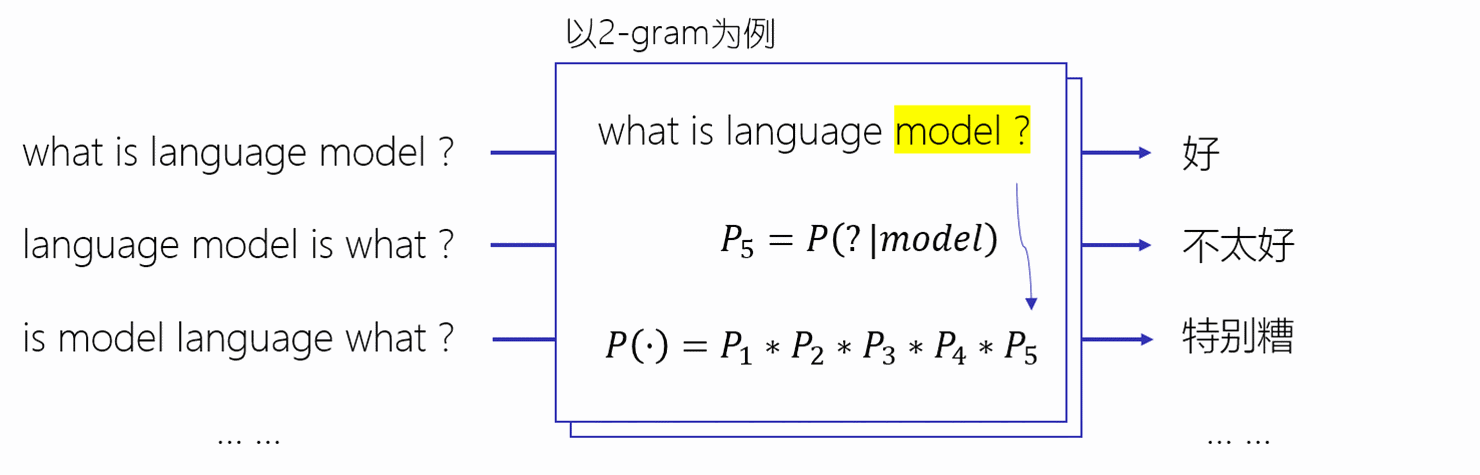
在自然语言处理中最为核心的就是语言模型(LM)。因此,学习语言模型是自然语言处理中的重中之重。在介绍语言模型之前,我们首先给大家介绍Nosiy Channel Model以及Chain Rule。
Nosiy Channel Model
这里给大家介绍一个公式:
![]()
其实这个公式是根据贝叶斯公式推出来的,具体推导如下:

主要的应用场景在于语音识别、机器翻译、拼写纠错、OCR识别以及密码破解。通过这些应用我们不难发现:其实这些应用都有一个共同点:那就是给定一段信号,将其转化为文本的形式。这几种应用的过程其实就是以上这个公式的具体应用。具体如下:

Chain Rule
首先给大家一个联合分布公式,这是Chain Rule的基础公式:

同理:我们给定A,B,C,D,则有:
![]()
这个其实我们可以给出证明,在证明中,用到的核心的公式就是概率联合分布的公式。并且有一点很重要,那就是在证明过程中不断将其复杂的多个字母看做一个整体,其实就是我们之前的换元,这样会让我们的证明更加的清晰。具体证明如下:
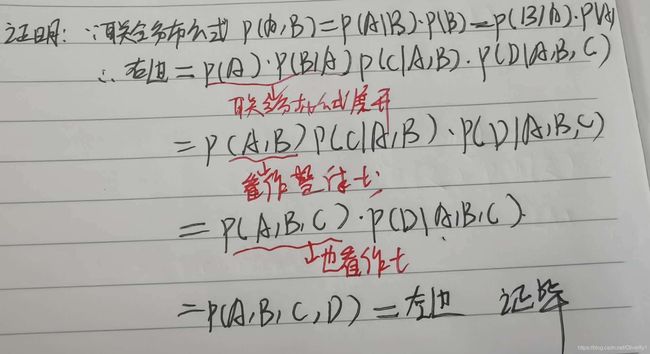
我们将其推广到一般的情况,即有如下的公式:
![]()
我们可以举个例子来说明这个Chain Rule的具体用法。
![]()
这里需要注意的是:P(是|今天)是表示“今天”的前提下,是“是”的概率,同理,P(春节|今天,是)表示“今天是”的前提下,出现“春节”的概率。假设给定以下一个语料:[今天是春节我们都休息…今天是春节我们都放假…]

这显然是有问题的,这也是Chain Rule的特点(缺点):后面的概率过于依赖前面的概率。也就是说只要有一个词不在语料库中,则整个的句子概率为0。并且也存在稀疏性问题,这也是语言模型中存在的一个问题,接下来给大家介绍语言模型。
语言模型(Language Model)
语言模型用来判断:是否一句话从语法上通顺。当然这是本人对语言模型通俗的理解。它的目标就是:Compute the probability of a sentence or sequence of words.用公式表示为:P(s) = P(w1,w2,w3,w4,w5…wn)。所用到的方式为给定一个句子,计算该句子在当前LM下的概率。重点是LM的训练。这个LM的训练用到的就是前面提到的Noisy Channel Model以及Chain Rule以及后面介绍的Markov Assumption和Unigram, Bigram, N-gram等方式。接下来给大家介绍一个很著名的Markov Assumption。
Markov Assumption(马尔科夫假设)
在深度学习中,大家一定对隐马尔科夫模型以及条件随机场很熟悉吧,它们都是基于马尔科夫假设。马尔科夫假设是用来估计两个模型之间的近似概率。接下来给大家介绍first order、secod order以及third order Markov Assumption计算公式:

我们举个例子来详细说明该模型怎么应用。
例如:P(休息|今天,是,春节,我们,都)
- P(休息|都) ===>1st order Markov Assumption
- P(休息|我们,都) ===>2nd order Markov Assumption
- P(休息|春节,我们,都) ===>3rd order Markov Assumptio
如果给定一个训练好的Language Model,列出了以下概率:
P(是|今天)=0.01
P(今天)=0.002
P(周日|是)=0.001
P(周日|今天)=0.0001
P(周日)=0.02
P(是|周日)=0.0002
我们使用 1st order Markov Assumption来计算今天是周日 VS 今天周日是的概率,则:
P(今天 是 周日) = P(今天)·P(是|今天)·P(周日|是) = 0.002×0.01×0.001=2×10^(-8) P(今天
周日 是) = P(今天)·P(周日|今天)·P(是|周日) = 0.002×0.0001×0.0002=4×10^(-10)
可以得知:P(今天 是 周日) > P(今天 周日 是),即P(今天 是 周日) 的语义更好,当然事实上也符合我们的正常的语法。这就是马尔科夫假设在语言模型中的应用。
Unigram Bigram N-gram
1、Unigram
Unigram其实就是最简单的独立假设。每个单词都是独立的,没有考虑语义。假设W_1,W_2,W_3,W_4,…,W_n是句子分词的结果,则有:
![]()
我们通过一个例子来说明这个问题,例如
P(今天,是,春节,我们,都,休息) = P(今天)·P(是)·P(春节)·P(我们)·P(都)·P(休息)
P(今天,春节,是,都,我们,休息) = P(今天)·P(春节)·P(是)·P(都)·P(我们)·P(休息)
从上面的例子可以看出,句子的顺序不一样,但是正常通过unigram计算后的P都一样,所以这样并不能很好的区分语义。我们再来看一个例子。

我们通过计算可知,由于在词库中没有“一起”,结果导致该项的概率为0,实际上这是不可能的。接下来给大家介绍Bigram。
2、Bigram
由于前面的Unigram模型没有考虑语义,因此Bigram考虑到与前1个单词的顺序,这里可以判断语义。假设W_1,W_2,W_3,W_4,…,W_n是句子分词的结果,则有:

3、N-gram
前面我们介绍了Unigram以及Bigram,接下来给大家介绍N-gram,这里需要说明的是,尽管这里介绍的是N-gram,但是,一般我们的n不会超过7,最常用的就是前面介绍的这样中模型,即n=0,1的时候。接下来我们n=2,也就是考虑到与前2个单词的顺序,因此可以判断语义。假设W_1,W_2,W_3,W_4,…,W_n是句子分词的结果,则有:
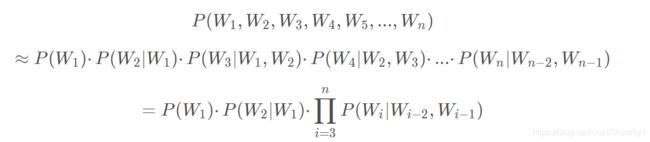
估计语言模型的概率(Estimating Probability of Language Model)
1、Unigram:Estimating Probability
接下来我们介绍如何通过独立模型去估计语言模型的概率。以下是其公式:
P(Wn) = 词汇Wn出现次数 / 语料库所有词汇数量V。即:
![]()
2、Bigram:Estimating Probability
p(w1,w2,w3,w4…wn) = p(w1)* p(w2|w1)* p(w3|w2,w1)…p(Wn|Wn-2,Wn-1)。P(Wn/Wn-2,Wn-1) = 出现Wn的同时也出现词汇Wn-1,Wn-2的次数 / 词汇Wn出现次数。这里需要注意的是:对于其中一项概率为0,可以作平滑处理。
评估语言模型(Evaluation of Language Model)
前面我们介绍了如何去估计一个语言模型的概率,那么如何评估我们估计的一个语言模型的是好是坏呢?
在理想的情况下:
1、假设有两个语言模型A,B
2、选定一个特定的任务比如拼写纠错
3、把两个模型A,B都应用了此任务中
4、最后比较准确率,从而判断A,B的表现。
Perplexity
我们给出Perplexity的表达式为Perplexity = 2(-x),其中的x : average log likelihood。具体计算过程如下:
- 将训练好的 LM 放入 语料库,计算 likelihood。
- likelihood 的越大,x越大,2^(-x) 越小,Perplexity越小,越小越好!!
- Perplexity 尤其适用 unsupervised 文本的情况
接下来我们介绍Perplexity的计算。Perplexity = 2(-x),其中的x : average log likelihood (平均 对数 似然)。我们计算X 的过程:
- likelihood : 计算P(Wn)
- log likelihood: 计算logP(Wn)
- average log likelihood: x = (logP(W1)+…+logP(Wn))/n
- 最后将x带入Perplexity公式。
我们接下来用一个案例来加深对其计算过程的理解:我们给出以下语言模型以及需要评估的句子,接下来计算x。

具体的计算过程如下:

我们将其训练集达到38 million words,测试集为1.5million words,对比其N-gram Order、Unigram、Bigram以及Trigram,结果如下:

从上面的结果可以看出:一般情况下,N-gram LM 效果更好。
总结
本文主要介绍了NLP中最重要的核心——语言模型(LM),在此之前首先给大家补充了Noisy Channel Model以及帮大家回顾了概率中的Chain Rule规则。并且我们介绍了语言模型的概念以及通过马尔科夫假设和Unigram, Bigram, N-gram,并且通过这些方法的计算,我们发现无论用那种方式,只要语料库中没有一个单词,导致整个句子的概率为0,这是很不正常的,这是语言模型中的一个问题,还有就是稀疏性问题。下一篇文章我们会给大家解决本文章留下来的语言模型的这个问题——稀疏性问题,首先给大家剧透一下,这里用到的是平滑技术。今天的文章就写在这里,希望对大家理解语言模型的理解有一定的帮助。最后送大家一句话“Inspire Aspire Unitl i Expire——生命不息,奋斗不止”。