leetcode题解-2020.03.29(题目编号1/892/914/999/820/1162/2/3)
文章目录
- 前言
- 1 两数之和
- 题目描述
- 思路解析
- 示例代码
- 892 三维形体的表面积
- 题目描述
- 思路解析
- 示例代码
- 914 卡牌分组
- 题目描述
- 思路解析
- 示例代码
- 999 可以被一步捕获的棋子数
- 题目描述
- 思路解析
- 示例代码
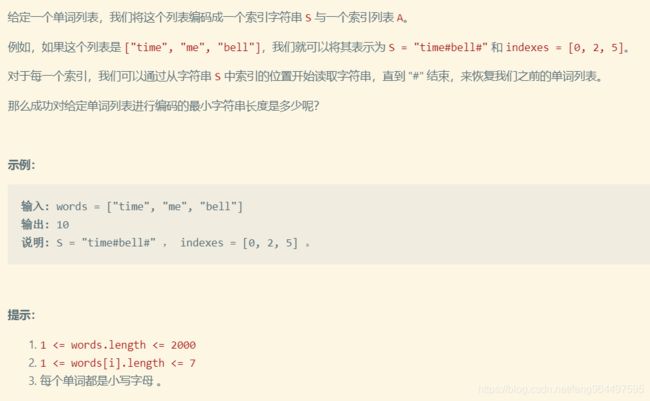
- 820 单词的压缩编码
- 题目描述
- 思路解析
- 示例代码
- 1162 地图分析
- 题目描述
- 思路解析
- 示例代码
- 2 两数相加
- 题目描述
- 思路解析
- 示例代码
- 3 无重复字符的最长子串
- 题目描述
- 思路解析
- 示例代码
前言
本周完成的题目有:
- 1 两数之和(简单难度)
- 892 三维形体的表面积(简单难度,每日一题)
- 914 卡牌分组(简单难度,每日一题)
- 999 可以被一步捕获的棋子数(简单难度,每日一题)
- 820 单词的压缩编码(中等难度,每日一题)
- 1162 地图分析(中等难度,每日一题)
- 2 两数相加(中等难度)
- 3 无重复字符的最长子串(中等难度)
博客专栏地址:https://blog.csdn.net/feng964497595/category_9848847.html
github地址:https://github.com/mufeng964497595/leetcode
1 两数之和
题目描述
给定一个整数数组 nums 和一个目标值 target,请你在该数组中找出和为目标值的那两个整数,并返回他们的数组下标。
你可以假设每种输入只会对应一个答案。但是,你不能重复利用这个数组中同样的元素。
示例:
给定 nums = [2, 7, 11, 15], target = 9
因为 nums[0] + nums[1] = 2 + 7 = 9
所以返回 [0, 1]
思路解析
- 一般题目拿到手,先考虑最简单的暴力算法。题目要找数,而且只找两个,那就很简单地用两个for循环嵌套遍历一波,把两两组合都算出来就可以了,注意别重复取同一个数了,例如输入[1,2,3],要找4,就不能返回[1, 1],而要返回[0, 2]。
- 暴力算法之外,有没有更快一点的?当然有啦。题目输入是一个数组,要我们输出下标,那一般就是要把数值的值和下标记录起来。所以,我们可以用一个map来记录值与下标的关系,把数组的值和下标都放到map里,然后遍历map,看目标值-当前遍历到的值是不是也在map中,且与当前遍历到的值不在同一个位置,如果是的话,那就找到结果了。
- 方法2有没有问题?当然有=_=||。考虑这样一组用例:[1,3,3,2],目标值是6,那么在预处理的时候,map对于key相同的值会用后插入的结果来覆盖掉,所以map里面其实只有一个3,那么就会error啦。那可能会想到,使用multimap是不是能解决?答案是可以的,不过代码写起来会有点恶心,因为multimap查找key只会返回找到的其中一个值,没办法把所有key相同的结果都返回回来,要自己去搜,这性能就有点影响了。
- 那要怎么解决呢?其实很好办。我们前面是先预处理数组里的值到map中,才会有这个冲突的问题,那如果我们不预处理,而是先把map置为空,然后遍历数组,看目标值-当前遍历到的值是否在map中,如果不在,就插入map,在的话,那就是找到结果了,而且也不存在找到的两个值是同一个下标的情况。这样就解决上面的冲突问题啦。
- 可能有同学会问,对于key相同的情况,在map上不是依旧会冲突吗?其实不然。按题目的描述,一次只会有一个答案,那么对于key相同且其中一个下标是答案的一部分的情况,就只会是key相同的两个下标都是答案,且只会有两个key相同的下标,否则就跟题目的描述冲突了。既然只会有这种情况,而我是边遍历数组边插入map,那么就不存在这两个key都在map中这种情况了。
示例代码
class Solution {
public:
vector twoSum(vector& nums, int target) {
// 用map来记录已搜索过的值&对应的下标
std::map mVal2Idx;
vector vRes;
// 提前分配空间,避免push_back触发空间重新分配,影响性能
vRes.reserve(2);
int size = nums.size();
for (int i= 0; i < size; ++i) {
int val = target - nums[i];
auto mit = mVal2Idx.find(val);
if (mVal2Idx.end() == mit) {
// 没找到,将数组当前值送入map
mVal2Idx.insert(std::make_pair(nums[i], i));
} else {
// 从map中找到另一个值,那就得到结果了。
// 对于数组中有两个值相同的情况也兼容了,
// 因为题目说只有一个答案,那么如果出现两个值相同且其中一个是答案的情况,
// 就只能是这两个值都是答案这一种可能。
// 而此时map里只有一个值,所以不存在下标被覆盖的情况
// mit->second比较小,放前面
vRes.push_back(mit->second);
vRes.push_back(i);
break;
}
}
return vRes;
}
};
892 三维形体的表面积
题目描述
在 N * N 的网格上,我们放置一些 1 * 1 * 1 的立方体。
每个值 v = grid[i][j] 表示 v 个正方体叠放在对应单元格 (i, j) 上。
请你返回最终形体的表面积。
思路解析
- 算表面积,暴力算法就不太能搞了,要换换思路当成是智力题
- 假设,只有一列111的正方体,共n个,那么表面积怎么算呢?发挥下想象力,n个正方体竖着叠在一起,那么有四个侧面,每个侧面有n个11的面,那么侧面表面积就有4n,再加上上下两个面,所以表面积是4*n+2。(这里说的n>0哈)
- 如果每列正方体都没叠在一起,共m列,那么总的表面积也就可以算了,把每一列都套入公式算一下就好了。
- 但是题目这样出了,就肯定有一些叠在一起的,那么我们就用总的表面积来减去叠在一起的表面积就好了。那要怎么算那些叠在一起的呢?
- 单独看一列正方体,它被别人挡住的情况就只会出现在上下左右这四个方向,每个方向挡掉的表面积就是看谁矮了。例如一列有4个正方体,另一列有3个,两列并排放,那对于我这一列,就是挡掉3个嘛。
- 那么思路就清晰了:遍历网格的每一列,计算4*grid[i][j]+2得到这一列没被挡的总表面积(grid[i][j]=0就不用算了,直接跳过)。然后在分别比较一下grid[i][j]与它相邻的四个方向,减去小的那个高度,就得到当前列最终的表面积了。每一列都这样算就ok了。
- 是不是可以再优化一下呢?想想看哈,例如我们从i=0~n-1,j=0-n-1来遍历每一个网格,在访问它的四个方向的时候,对于当前列的左、下两个方向要减去的表面积,其实已经在计算左边这一列和下面这一列的时候就计算出来了,没必要再计算一次(两列并在一起,他们互相挡掉的表面积是一样的),在减去的时候*2就可以不用再浪费时间去再算一次左、下两个方向了。这可省掉了一半的时间。
示例代码
class Solution {
public:
int surfaceArea(vector>& grid) {
int n = grid.size();
int dirx[] = {0, 1}, diry[] = {1, 0};
int ans = 0;
for (int i = 0; i < n; ++i) {
for (int j = 0; j < n; ++j) {
// 当前格子没有正方体,不用处理
if (0 == grid[i][j]) continue;
ans += grid[i][j] * 4 + 2; // 四个面+上下底面
// 查找当前格子右边和上面相邻的两个格子,减去重复的区域。
for (int k = 0; k < 2; ++k) {
int x = i + dirx[k], y = j + diry[k];
if (x >= n || y >= n) continue;
// 两列都被挡住,所以减去的表面积要*2
ans -= std::min(grid[i][j], grid[x][y]) * 2;
}
}
}
return ans;
}
};
914 卡牌分组
题目描述
给定一副牌,每张牌上都写着一个整数。
此时,你需要选定一个数字 X,使我们可以将整副牌按下述规则分成 1 组或更多组:
- 每组都有 X 张牌。
- 组内所有的牌上都写着相同的整数。
仅当你可选的 X >= 2 时返回 true。
示例 1:
输入:[1,2,3,4,4,3,2,1]
输出:true
解释:可行的分组是 [1,1],[2,2],[3,3],[4,4]
思路解析
- 其实题目搞那个“可行的分组”就是来吓人的,他只要你输出true或者false,而不需要输出具体要怎么分组,别想着去计算具体要怎么分,否则会陷入一条不归路。
- 分组要分出每组有X张牌,且组内的牌面要相同,那么就要先统计一下每个牌面有几张牌。
- 统计完成后,每个组都需要有x张牌,且分组的数量不限,那么对于牌面1有n1张牌,n1肯定要能被x整除,即n1是x的倍数。对于牌面2有n2张牌,n2也必须是x的倍数。依此类推,也就是说,x是所有牌面张数的倍数,这个概念熟不熟悉?换个名词就是,x是所有牌面张数的公约数。题目要求有超过1个不同的x时返回true,也就是这些牌面张数的公约数超过1个。又已知1是所有非0整数的公约数,那么答案就很明显啦,这些牌面张数的最大公约数大于1,就返回true,否则就返回false。
- 最大公约数怎么求呢?辗转相除法就ok啦,这里主要讲题解思路,求最大公约数在网上的介绍也很多,就不详细介绍了。
示例代码
class Solution {
public:
bool hasGroupsSizeX(vector& deck) {
// 用map统计每个数字有几张牌
std::map mCard2Num;
for (auto val : deck) {
++mCard2Num[val];
}
// 计算各个数的最大公约数,大于1就表示有超过一种分配方法
int gcd = 1;
bool first = true;
for (auto item : mCard2Num) {
if (first) {
// 第一个数是自己的最大公约数
gcd = item.second;
first = false;
} else {
// 计算最大公约数
gcd = CalcGCD(gcd, item.second);
}
if (1 == gcd) break;
}
return gcd > 1;
}
private:
int CalcGCD(int a, int b) {
return b == 0 ? a : CalcGCD(b, a % b);
}
};
999 可以被一步捕获的棋子数
题目描述
题目太长了,就转述一下。
题目意思大概就是,R可以往上下左右这四个方向一直走,只要走到边界、遇到B、遇到p就停止。问有多少个p是R走一步就可以吃到的。
思路解析
- 直接照着做就好了,水题一道。。。
- 第一步肯定是先找到R在哪个位置啦
- 找到之后呢,往上走一走,走到边界、遇到B、遇到p就停止,看看能不能遇到p,如果遇到了,就计数+1。另外三个方向也一样。
示例代码
class Solution {
public:
int numRookCaptures(vector>& board) {
// 找车在哪
int n = board.size();
int x, y;
bool bFind = false;
for (int i = 0; !bFind && i < n; ++i) {
for (int j = 0; !bFind && j < n; ++j) {
if ('R' == board[i][j]) {
x = i; y = j;
bFind = true;
}
}
}
if (!bFind) return 0;
// 四个方向都走一走,撞到边界、自家人、敌军就可以停了
int ans = 0;
int dirx[] = {0, 1, 0, -1}, diry[] = {1, 0, -1, 0};
for (int i = 0; i < 4; ++i) {
int new_x = x + dirx[i];
int new_y = y + diry[i];
while (new_x >= 0 && new_x < n && new_y >= 0 && new_y < n) {
if ('B' == board[new_x][new_y]) break;
if ('p' == board[new_x][new_y]) {
++ans;
break;
}
new_x += dirx[i];
new_y += diry[i];
}
}
return ans;
}
};
820 单词的压缩编码
题目描述
思路解析
- 题目乍一看是要算字符串子串问题,但分析一下,如果字符串a是字符串b的一部分,且不是后缀,那么以"abc"、“dabcd"为例,按照题目的意思就会压缩成"dabc#d#”,但是这样的话,字符串"dabcd"就断开了,因此这种情况是不符合题意的。也就是说,只有当字符串a是字符串b的后缀,才符合题意。因此这道题其实是要字符串后缀问题。
- 单词总数2000个,单词长度7,那么直接暴力解法,两个for循环嵌套计算,把整个单词都是任意一个其它单词的后缀的单词去掉,其余剩下来的n个单词的总长度加上n个#号符就是最小字符串长度了。
- 除了暴力算法还有没有别的解法呢?看到字符串后缀,很自然地就想到用后缀树来处理。
这里简单介绍一下后缀树。后缀树,简单理解的话,就是用字符串的后缀拼成一棵树,这样相同后缀的字符串就会共用一部分节点,那么组成后缀树之后,对于那种整个字符串都是某个字符串的后缀的这种情况,就会隐藏在树中间,最后统计这棵树的每条路有多长,答案就是多少了。
以字符串"abcd"、“bbcd”、“abc”、“bcd"为例组成后缀树,那么就是:
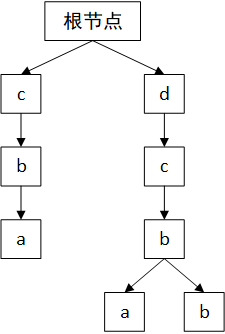
遍历这棵树的每条路,就是"cba”、“dcba”、“dcbb”,原本的字符串"bcd"很自然地就被隐藏掉了。 - 建完树再来遍历,总觉得会慢了点,可不可以在建树的时候就顺便统计呢?当然可以嘿嘿嘿。还是以字符串"abcd"、“bbcd”、“abc”、“bcd"为例(以下文字描述对应看看上面的图会容易理解些)。初始时树是空的,那么对于字符串"abcd"的每个字符都是新增的节点,所以字符串"abcd"就是最终后缀树的一条路了,此时长度就是4+1=5(加上#号)。接下来处理字符串"bbcd”,后缀"bcd"都是现有的节点,就直接顺着树往下走,最后一个字符’b’不存在这个节点,就新增节点’b’。由于"bbcd"这个字符串有新增节点,也就是说字符串"bbcd"不是现有任一字符串的后缀,所以现在的长度就是5+(4+1)=10。接下来处理字符串"abc",同理,不是后缀串,现在的长度是10+(3+1)=14。最后处理字符串"bcd",发现整个字符串的节点在后缀树里面都有了,也就是说字符串"bcd"是现有某一个字符串的后缀,那么就不需要加上这个字符串的长度了,所以答案是14+0=14。
- 上面这个解法有没有问题呢?当然有=_=||。考虑"bcd"、“abcd"这个例子,按照上面的解法,先以"bcd"建树,此时有新建节点,故长度是3+1=4,再处理字符串"abcd”,也有新建节点,故长度是4+(4+1)=9。而其实答案是5。而把字符串反过来,先处理"abcd",再处理"bcd",得出来的长度就是5了。那要怎么办呢?一种方法是在后缀树上标记一下每个字符串的终结标记,如果插入新的字符串的时候,发现走到了一个含有终结标记的节点,就把计算出来的长度减掉根节点到这个终结标记节点的长度,并抹掉这个终结标记。另一种方法就是先把字符串数组按字符串长度递减的顺序排序,再进行步骤4,就ok了。
示例代码
这里只展示使用终结标记的代码
class Solution {
public:
int minimumLengthEncoding(vector& words) {
int ans = 0;
SuffixTree root;
for (auto word : words) {
int len = word.size();
SuffixTree* pNode = &root; // 用来遍历的指针
int layer = 0;
bool isSuffix = true; // 标记当前字符串是否是后缀串
for (int i = len - 1; i >= 0; --i) {
++layer;
auto& next = pNode->next;
if (next.find(word[i]) != next.end()) {
// 使用现有节点
pNode = next[word[i]];
} else {
// 创建新节点
SuffixTree* pNewNode = new SuffixTree();
next.insert(std::make_pair(word[i], pNewNode));
pNode = pNewNode;
isSuffix = false;
}
if (pNode->isEnd && i != 0) {
// 当前节点有是某个字符串的终结节点,减去这个字符串的长度
// 加上i!=0的判断,是因为这种情况下就意味着有两个字符串完全相同,
// 前面的处理逻辑本身就会将后加的字符串当成后缀给舍弃,就没必要减掉前面的字符串。
ans -= layer + 1;
pNode->isEnd = false;
}
}
if (!isSuffix) {
ans += layer + 1; // 加上#号的长度
pNode->isEnd = true; // 最后一个节点打上终结标记
}
}
return ans;
}
private:
// 后缀树节点
class SuffixTree {
public:
SuffixTree() : isEnd(false) {
}
~SuffixTree() {
for (auto item : next) {
Delete(item.second);
}
}
private:
// 释放内存
void Delete(SuffixTree* tree) {
if (!tree) return;
for (auto item : tree->next) {
Delete(item.second);
}
}
public:
std::map next; // 树的子节点
bool isEnd; // 字符串终结标记
};
};
1162 地图分析
题目描述
题目看起来挺绕的,其实就是两个概念在绕:
- 距离陆地区域最远的海洋区域。这个离陆地区域的距离怎么算呢?其实就是这块海洋到所有陆地的最短距离。把所有海洋到陆地的最短距离算出来,挑出一个距离最远的,就是目标海洋了。
- 该海洋区域到离它最近的陆地区域的距离。其实跟1是同一个东西,只不过题目不需要返回目标海洋的坐标,只需要返回距离。
思路解析
- 题目要问距离,而且求的是曼哈顿距离,而不是直线距离。看题目曼哈顿距离的概念,那么其实就等于是从陆地出发,走上下左右四个方向,走几步到达海洋,那么曼哈顿距离就是多少。看到这个,出于技术敏感性,很自然地就优先考虑一下bfs广度优先搜索了。
- bfs,从各块陆地出发,一步一步走,走的时候对已走过的区域打上标表示已走过不需要重复走,并记录走到对应区域用了几步,最后访问的那个区域就是目标海洋了,用的步数就是答案。
- 鉴于bfs是个基础算法,网上资料也多,这里也就不赘述了。
示例代码
class Solution {
public:
int maxDistance(vector>& grid) {
// 找出所有陆地的坐标,压入队列
int dwLandNum(0);
std::queue q;
// bfs visit标记,其实也可以用grid来打标就行了,但是破坏原始数据的这个习惯不太好
bool visit[105][105];
memset(visit, 0, sizeof(visit));
int n = grid.size();
for (int i = 0; i < n; ++i) {
for (int j = 0; j < n; ++j) {
if (1 == grid[i][j]) {
++dwLandNum;
q.push(Point(i, j, 0));
visit[i][j] = true;
}
}
}
// bfs搜索就行了,最后一个找到的海洋就是目标
int dirx[] = {0, 1, 0, -1}, diry[] = {1, 0, -1, 0};
int ans = -1;
while (!q.empty()) {
Point p = q.front();
q.pop();
for (int i = 0; i < 4; ++i) {
int x = p.x + dirx[i];
int y = p.y + diry[i];
if (x >= 0 && x < n && y >= 0 && y < n && !visit[x][y] && 0 == grid[x][y]) {
visit[x][y] = true;
ans = p.step + 1;
q.push(Point(x, y, ans)); // 压入队列
}
}
}
return ans;
}
private:
struct Point {
int x, y; // 坐标
int step; // 搜索到当前坐标所花费的步数
Point(int xx = 0, int yy = 0, int s = 0)
: x(xx), y(yy), step(s) {
}
};
};
2 两数相加
题目描述
题目讲的很直白了,就是给出两个数,已经按十进制按位拆出放到链表中,求这两个数相加得到的链表。
思路解析
模拟题,直接按照加法模拟照做就行了。因为我不想养成破坏原始数据的习惯,所以我新开了一个链表来保存计算结果。
题目有几个注意事项:
- 两个链表可能会有空指针(不知道测试样例有没有哈),如果有某一个链表是空指针,就直接return另一个链表指针就可以了。
- 两个链表的长度不一定一样长
- 两个链表都加完之后,可能还会有进位,需要处理一下。(例如9 + 2 会生成进位1).
示例代码
class Solution {
public:
ListNode* addTwoNumbers(ListNode* l1, ListNode* l2) {
// 任一链表为nullptr,直接返回另一个链表,不需要处理
if (!l1) {
return l2;
} else if (!l2) {
return l1;
}
ListNode* p1 = l1;
ListNode* p2 = l2;
// 为了不养成破坏原始数据的习惯,使用第三个链表来记录结果
ListNode* ans = nullptr;
ListNode* pNow = nullptr;
int add(0); // 上一步加法的增量
while (p1 && p2) {
int val = p1->val + p2->val + add;
DealVal(val, add);
if (!ans) {
ans = new ListNode(val);
pNow = ans;
} else {
ListNode* tmp = new ListNode(val);
pNow->next = tmp;
pNow = tmp;
}
p1 = p1->next;
p2 = p2->next;
}
// 走到这一步,已保证pNow、ans不是空指针
if (p1) {
AddList(p1, pNow, add);
} else {
AddList(p2, pNow, add);
}
// 最后可能还有加法的进位
if (0 != add) {
ListNode* tmp = new ListNode(add);
pNow->next = tmp;
}
return ans;
}
private:
void DealVal(int& val, int& add) {
if (val >= 10) {
// 向前进位
val -= 10;
add = 1;
} else {
add = 0;
}
}
void AddList(ListNode*& pList, ListNode*& pRes, int& add) {
while (pList) {
int val = pList->val + add;
DealVal(val, add);
ListNode* tmp = new ListNode(val);
pRes->next = tmp;
pRes = tmp;
pList = pList->next;
}
}
};
3 无重复字符的最长子串
题目描述
思路解析
-
题目乍一看是字符串子串问题,但其实不是。这道题换个马甲,改成求数组中无重复数字的最长连续区间长度,也是一样的道理,别被骗了然后一直往字符串算法上面去套。
-
因为做过挺多算法的,所以看到这种最长连续区间类型的题目,很自然就想到尺取法。你要是问我怎么就能想到这个算法,我也解释不上来,可能是打ACM培养出来的敏感性吧。。。。下面以字符串"pwekwp"为例演示一下尺取法。
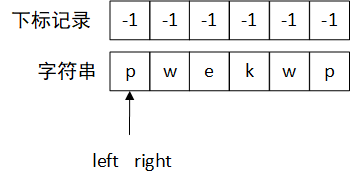
初始如上图所示。尺取法有left、right两个指针,用来像尺子一样丈量数组。下标记录数据是用来标记已访问过的字符对应的下标,有两个作用,一个是标记哪些字符已访问,另一个是方便快速找到字符对应的上一个下标。
初始时left、right指向同一个字符,长度就是1啦,更新下标记录。这时候right指针右移,得到下图: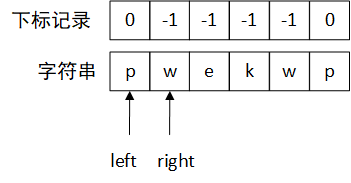
此时right指针对应的下标记录为-1,表示未访问过,那此时长度就是right-left+1=2了。再更新一下w的下标,right指针右移。同理,省略掉right指针在e、k的情况,直接演示下一个w的情况。注意一点就是,right指针右移的时候更新当前的最新长度。移动到下一个w时,最新长度已经是4了。
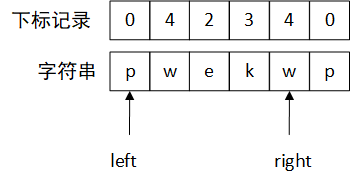
w对应的下标记录是1,且在left ~ right之间,那就说明left ~ right已经遇到重复的字符了,这时候把left指针移动到w下标记录+1的位置,也就是第一个e的位置,并将w的下标记录改为right的位置。然后更新当前的长度。由于right - left + 1 = 3 < 4,所以不需要更新。之后再继续把right指针右移。
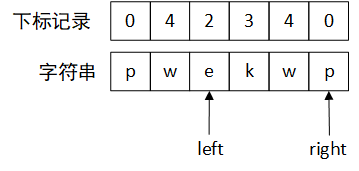
这时候发现right对应的字符p已经有了下标记录,但是下标记录不在left ~ right中间,依旧认为是没有重复字符,更新长度,right指针右移。此时right指针已经超出范围了,可以结束了。(为什么不需要再看left指针右移呢?因为left ~ right已经没有重复字符了,left指针右移的长度肯定比现在的要短,就没必要浪费时间去算了) -
从上面介绍的步骤可以看出,使用尺取法,只需要遍历一次字符串即可,时间复杂度O(n),很快速,实现起来也很简单。
示例代码
class Solution {
public:
int lengthOfLongestSubstring(string s) {
int pos[256+5]; // 保存字符与下标的映射,字符ASCII码就那几百个
memset(pos, -1, sizeof(pos));
int len = s.length();
int left = 0, right = 0;
int ans = 0;
while (right < len) {
if (left == right) {
// 指向同一个字符,记录下标,右指针右移
pos[s[left]] = left;
++right;
ans = std::max(ans, 1);
} else {
if (pos[s[right]] != -1 && pos[s[right]] >= left) {
// 发现left~right中间的重复字符,right - left就是不重复字符串的长度
ans = std::max(ans, right - left);
// 左指针移动到重复字符的右边一位,避开这个重复字符
left = pos[s[right]] + 1;
} else {
// 未发现重复字符,更新当前长度
ans = std::max(ans, right - left + 1);
}
// 更新下标,右指针右移
pos[s[right]] = right;
++right;
}
}
return ans;
}
};