线段树基础入门详解（适用于初学者）

由于以前看多了各种博客，关于线段树的讲解总是十分冗长，因此特此作文，大概讲解基本概念及操作。初次写博，多多包涵

一、线段树的概念
线段树在各个节点保存一条线段（数组中的一段子数组），主要用于高效解决连续区间的动态查询问题，由于二叉结构的特性，它基本能保持每个操作的复杂度为O(logn)。（看不懂不用管，没啥用）

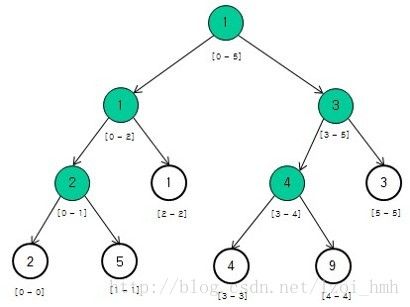
这个图是线段树求数组array[2, 5, 1, 4, 9, 3]的区间最小和的例子（看不懂没关系，下面解释）。

图中每个节点下面那个中括号里[a-b]意为该节点表示数组array从array[a]到array[b]的范围内的最小值（节点中间那个数就是最小值，可以把array自己手动试一试）。这个地方有点类似二分的思想，父亲的区间是[a,b]，那么(c=(a+b)/2)左儿子的区间是[a,c]，右儿子的区间是[c+1,b]（所有的线段树都必须遵循这个规律，这主要是为了在后边的操作中方便搜索，先不用管）

如图可见每个节点所代表的范围就是2个儿子的范围加起来，那么它的值也就是两个儿子值中较小的那个（本例子求的是最小值）（总体来说：一层一层从叶节点往上不断扩大答案的范围，叶节点只是适用于原始数组中的单个数据的答案（如果按照上面的例子，也就是一个数的最小值，它本身），在中间得到适用于数组中某一段的答案（某一段中的最小值），到了顶上根节点就得到适用于整个数组的答案了（整个数组中的最小值），这里要抽象地想一想这个过程，就会有所领悟）

通过同样的方式，只需要一点点改动，也就能实现求区间最大值，区间和等功能。

二、线段树的基本操作（附带详细注释版）
(1)：线段树的构造
void build(int node, int begin, int end),主要思想是递归构造，如果当前节点记录的区间只有一个值，则直接赋值，否则递归构造左右子树，最后回溯的时候给当前节点赋值

#include   
using namespace std;  

const int maxind = 256;  
int segTree[maxind * 4 + 10];    //segtree用于存放线段树
int array[maxind];     //array用于存放原始数组
/* 构造函数，得到线段树 */  
void build(int node, int begin, int end)    
{    
    if (begin == end)    
  {      segTree[node] = array[begin]; /* 只有一个元素,节点记录该单元素 */ 
  return;   
}
    else    
    {     
        /* 递归构造左右子树 */   
        build(2*node, begin, (begin+end)/2);    //查找左孩子
        build(2*node+1, (begin+end)/2+1, end);   //查找右孩子

        /* 回溯时得到当前node节点的线段信息 */    
        if (segTree[2 * node] <= segTree[2 * node + 1])     //选取最小值
            segTree[node] = segTree[2 * node];    
        else    
            segTree[node] = segTree[2 * node + 1];    
    }    
}  

int main()  
{  
    array[0] = 1；
  array[1] = 2；
  array[2] = 2；
  array[3] = 4；
  array[4] = 1；
  array[5] = 3;  
    build(1, 0, 5);  
    for(int i = 1; i<=20; ++i)  
     cout<< "seg"<< i << "=" <return 0;  
}   

我们上面讲的父亲和儿子节点表示范围的规律在这里就运用了

(2)：区间查询
int query(int node, int begin, int end, int left, int right);
（其中node为当前查询节点，begin,end为当前节点存储的区间，left,right为此次query所要查询的区间）
主要思想是把所要查询的区间[a,b]划分为线段树上的节点，然后将这些节点代表的区间合并起来得到所需信息
比如前面一个图中所示的树，如果询问区间是[0,2]，或者询问的区间是[3,3]，不难直接找到对应的节点回答这一问题。但并不是所有的提问都这么容易回答

int query(int node, int begin, int end, int left, int right)    //以后所有的查找都是从根结点开始
{   
    int p1, p2;    

    /*  当前查询区间和要求的区间没有交集  */  
    if (left > end || right < begin)    
        return 0x7ff;    

    /*  如果当前查询区间包含在要求的区间中，子集 */      
    if (begin >= left && end <= right)    
        return segTree[node];    

    /*  如果当前查询区间和要求区间有交集，但不是子集  */  
       p1 = query(2 * node, begin, (begin + end) / 2, left, right);   //查找左子树
    p2 = query(2 * node + 1, (begin + end) / 2 + 1, end, left, right);  //  查找右子树

    /*  返回较小值  */     
    if (p1 <= p2)    
        return  p1;    
    return  p2;      
}   

可见，这样的过程一定选出了尽量少的区间，它们相连后正好涵盖了整个[left,right]，没有重复也没有遗漏。同时，考虑到线段树上每层的节点最多会被选取2个，一共选取的节点数也是O(log n)的，因此查询的时间复杂度也是O(log n)。
线段树并不适合所有区间查询情况，它的使用条件是“相邻的区间的信息可以被合并成两个区间的并区间的信息”。即问题是可以被分解解决的。

（3）单节点更新
这里与前面查询方法类似，只不过反过来了

void Updata(int node, int begin, int end, int ind, int add)/*node:当前搜索到的元素在线段树中的下标 
                                                        add:加上的数值
                                                        [begin,end]：当前节点表示的区间
                                                        ind：待更新的节点在原始数组中的下标*/    
{    

    if( begin == end )    //找到了这个节点，更新
    {    
        segTree[node] += add;    
        return ;    
    }    
    int m = ( begin + end ) /2;    //计算中间值
    if(ind <= m)    
        Updata(node * 2,begin, m, ind, add);    //在左子树中更新
    else    
        Updata(node * 2 + 1, m + 1, end, ind, add);    //在右子树中更新
    /*回溯更新父节点*/    
    segTree[node] = min(segTree[node * 2], segTree[node * 2 + 1]);     //搜索完左右子树后，回溯当前节点

}   

（4）区间更新（线段树中最有用的）
需要用到延迟标记，每个结点新增加一个标记，记录这个结点是否被进行了某种修改操作(这种修改操作会影响其子结点)。对于任意区间的修改，我们先按照查询的方式将其划分成线段树中的结点，然后修改这些结点的信息，并给这些结点标上代表这种修改操作的标记。在修改和查询的时候，如果我们到了一个结点p，并且决定考虑其子结点，那么我们就要看看结点p有没有标记，如果有，就要按照标记修改其子结点的信息，并且给子结点都标上相同的标记，同时消掉p的标记。（但这样运算，就需要对整个程序进行修改，代码如下）

const int INFINITE = INT_MAX;
const int MAXNUM = 1000;
struct SegTreeNode
{
    int val;
    int addMark;//延迟标记
}segTree[MAXNUM];//定义线段树

/*
功能：构建线段树
root：当前线段树的根节点下标
arr: 用来构造线段树的数组
istart：数组的起始位置
iend：数组的结束位置
*/
void build(int root, int arr[], int istart, int iend)
{
    segTree[root].addMark = 0;//----设置标延迟记域
    if(istart == iend)//叶子节点
        segTree[root].val = arr[istart];
    else
    {
        int mid = (istart + iend) / 2;
        build(root*2+1, arr, istart, mid);//递归构造左子树
        build(root*2+2, arr, mid+1, iend);//递归构造右子树
        //根据左右子树根节点的值，更新当前根节点的值
        segTree[root].val=min(segTree[root*2+1].val,segTree[root*2+2].val);
    }
}
/*
功能：当前节点的标志域向孩子节点传递
root: 当前线段树的根节点下标
*/
void pushDown(int root)
{
    if(segTree[root].addMark != 0)//有做过更改
    {
        //设置左右孩子节点的标志域，因为孩子节点可能
        //被多次延迟标记又没有向下传递
        //所以是 “+=”
        segTree[root*2+1].addMark += segTree[root].addMark;
        segTree[root*2+2].addMark += segTree[root].addMark;
        //根据标志域设置孩子节点的值。因为我们是
        //求区间最小值，因此当区间内每个元
        //素加上一个值时，区间的最小值也加上这个值
        segTree[root*2+1].val += segTree[root].addMark;
        segTree[root*2+2].val += segTree[root].addMark;
        //传递后，当前节点标记域清空
        segTree[root].addMark = 0;
    }
}
/*
功能：线段树的区间查询
root：当前线段树的根节点下标
[nstart, nend]: 当前节点所表示的区间
[qstart, qend]: 此次查询的区间
*/

int query(int root, int nstart, int nend, int qstart, int qend)
{
    //查询区间和当前节点区间没有交集
    if(qstart > nend || qend < nstart)
        return INFINITE;
    //当前节点区间包含在查询区间内
    if(qstart <= nstart && qend >= nend)
        return segTree[root].val;
    //分别从左右子树查询，返回两者查询结果的较小值
    pushDown(root); //----延迟标志域向下传递
    int mid = (nstart + nend) / 2;
    return min(query(root*2+1, nstart, mid, qstart, qend),
               query(root*2+2, mid + 1, nend, qstart, qend));

}
/*
功能：更新线段树中某个区间内叶子节点的值
root：当前线段树的根节点下标
[nstart, nend]: 当前节点所表示的区间
[ustart, uend]: 待更新的区间
addVal: 更新的值（原来的值加上addVal）
*/
void update(int root, int nstart, int nend, int ustart, int uend, int addVal)
{
    //更新区间和当前节点区间没有交集
    if(ustart > nend || uend < nstart)
        return ;
    //当前节点区间包含在更新区间内
    if(ustart <= nstart && uend >= nend)
    {
        segTree[root].addMark += addVal;
        segTree[root].val += addVal;
        return ;
    }
    pushDown(root); //延迟标记向下传递
    //更新左右孩子节点
    int mid = (nstart + nend) / 2;
    update(root*2+1, nstart, mid, ustart, uend, addVal);
    update(root*2+2, mid+1, nend, ustart, uend, addVal);
    //根据左右子树的值回溯更新当前节点的值
    segTree[root].val = min(segTree[root*2+1].val, segTree[root*2+2].val);
}

三、经典例题