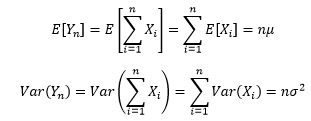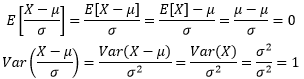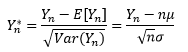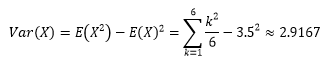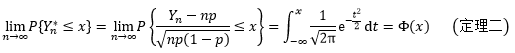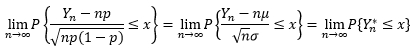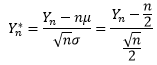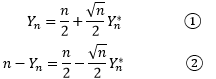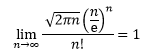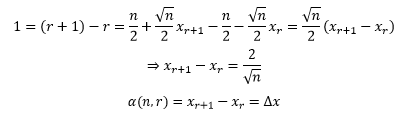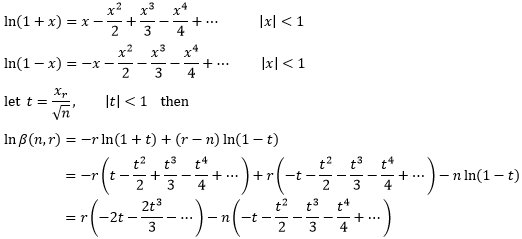概率统计19——中心极限定理
大数定律告诉我们,如果想要求得一个随机变量的期望,只需要进行多次重复试验,然后取均值就可以了。然而在使用大数定律时仍然需要小心,因为大数定律并没有明确指出到底需要多少次试验才能充分接近我们所期待的极限。无论实验多少次,我们仍然不能否认存在这样的情况:所抛出的骰子全部是同一点数,尽管这种情况发生的概率很小。
用Yn表示一系列独立同分布的随机变量X1, X2, …, Xn之和,既然X1, X2, …, Xn是随机变量,那么它们的和也是随机的。
一个令人惊奇的事实是,Yn的标准化形式总是趋近于正态分布。这意味着随机过程呈现出不确定性的表面下,其实是高度组织化的,所有随机变量最终都归于正态分布。这种现象就是中心极限定理的客观背景。
标准化处理
对于Yn来说,我们知道它的期望和方差:
为了简单起见,可以先假设μ=0,σ2 > 0,这样就可以认为Yn期望等于Xi的期望。
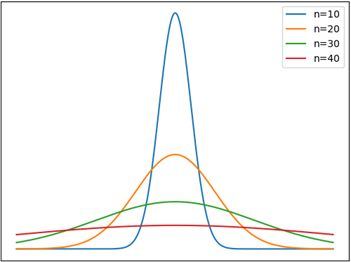
方差刻画了单个随机变量相对于均值的波动程度,类似地,我们也想要知道随机变量之和的波动,以便了解“骰子全部都是1点”这种小概率事件发生的几率。问题是,当n→∞时,Yn的方差是发散的:
![]()
随着n的增大,Yn的分布越来越均匀,在这种情况下讨论Var(Yn)没有任何意义:
Yn的分布越来越均匀
为了能够有效地讨论Yn的方差,需要对其进行标准化处理。
如果把变量做一个线性变换,可以发现下面的现象:
只要令X* = (X - μ)/σ,就可以让任意随机变量的期望化为0,方差化为1,这种转换称为标准化或归一化。
Yn的标准化是:
中心极限定理
中心极限定理告诉我们,如果有一个独立同分布的随机变量序列X1, X2, …, Xn,它们的期望为μ,方差为σ2>0,那么关于这些随机变量之和Yn的标准化变量Yn*的分布函数Fn(x),对于任意x满足:
想要证明这个定理并不容易,但我们可以在后文中给出一个从旁侧击的论据。
Yn*是Yn的标准化,二者的分布是一回事,因此中心极限定理的另一种写法是:
这里的~符号表示“近似于”。也就是说,对于均值为μ,方差为σ2>0的独立同分布的随机变量X1, X2, …, Xn之和Yn的标准化变量Yn*,当n充分大时,Yn* 趋近于均值为0,方差为1的正态分布:
![]()
我们可以把Var(Xi)看作一个微小的误差,Yn是微小误差的累加。中心极限定理告诉我们,当无数次微小误差的逐渐累加后,就会形成肉眼可见的巨大变化,并最终接近正态分布。
另外两种表达
在一般的情况下,很难求出Yn的分布函数,尤其是我们面对的经常是“小数”时。在现实生活中,这个“小数”常常就是1,因此才会说“不以成败论英雄”。但是当n充分大时,可以通过φ(x)给出其近似分布,这样就可以利用正态分布对Yn出现的概率进行分析。
把Yn*的分子和分母同时除以n:
于是得到了中心极限定理的另一种写法:
上一章我们计算了大数定律下均值的期望和方差:
由此,中心极限定理的第三种写法是:
以掷骰子为例,随机变量X是每次投掷骰子的结果,出现1~6点的概率都是1/6,E[X]=3.5,其方差是:
我们用程序模拟多次投掷骰子。每次试验投掷n次骰子,试验1000次,看看这种情况下点数均值的分布。
import numpy as np
import matplotlib.pyplot as plt
from scipy import stats
fig = plt.figure(figsize=(10, 5))
plt.subplots_adjust(hspace=0.5) # 调整子图之间的上下边距
mu, sigma_square = 3.5, 2.9167 # 骰子的期望和方差
xs = np.arange(0, 7, 0.01)
for i, n in enumerate([2, 10, 20, 50]):
ax = fig.add_subplot(2, 2, i + 1)
means = [np.random.randint(1, 7, n).mean() for i in range(1000)] # 生成1000组均值
sigma = np.sqrt(sigma_square / n)
ax.hist(means, bins=30, density=True, alpha=0.2, edgecolor='black', label='试验分布')
ys = stats.norm.pdf(xs, mu, sigma)
ax.plot(xs, ys, 'r--', label='$Y_n/n$~N($\mu,\sigma^2$)')
ax.set_xlabel('$Y_n/n, n={}$'.format(n))
ax.set_ylabel('pdf')
ax.legend(loc='upper right')
plt.rcParams['font.sans-serif'] = ['SimHei'] # 用来正常显示中文标签
plt.show()
n的值越大,Yn/n越趋近于N(μ,σ2/n)的正态分布。
示例
浙江大学《概率论与数理统计》中有一个很好的示例,直接贴图一下:
棣莫弗-拉普拉斯定理
我们通常讲的中心极限定理的全称是独立同分布中心极限定理。棣莫弗-拉普拉斯(De Moiver-Laplace)定理可以看作是独立同分布中心极限定理的窄化形式。
设Yn(n=1,2,…)服从参数为n,p(0 < p < 1)的二项分布Yn~B(n, p),Yn*是Yn的标准化,则对于任意x,有:
定理二是说,二项分布随机变量的标准化形式近似于均值为0,方差为1的正态分布。
根据二项分布的定义可知,Yn是n重伯努利事件中成功事件发生的次数。因此可以把Yn分解为n个伯努利随机变量之和,我们知道伯努利随机变量的期望是μ = p,方差是σ2 = p(1 - p),因此:
这和定理一的形式相同,既然相信定理一成立,那么定理二也成立。
用特例佐证
我们用成功率p=1/2的特例来检验棣莫弗-拉普拉斯定理,此时Yn~B(n, 1/2),根据二项分布的性质,我们也知道这特例条件下Yn的均值、方差和标准差:
由此可以得到Yn的标准化形式:
进一步可以用Yn*表示Yn:
现在进行简单的代数,假设当Yn = r时,Yn* = xr。由于Yn*是Yn的标准化,因此二者的概率是一样的,根据二项分布:
现在需要借助一下斯特林公式。
斯特林公式是一种适用于大数阶乘的近似公式。一般来说,当n很大的时候,n阶乘的计算量十分大,所以斯特林公式十分好用,而且,即使在n很小的时候,斯特林公式的取值也十分准确。
或更精确的:
将斯特林公式应用于③:
现在将r替换成xr,根据①和②:
xr可以用r和n表达,所以上式实际上是关于n和r的函数,由此我们做一个化简:
回顾定理二,可以知道:
现在1/√2π已经有了,我们的目标是让α和β趋近于合理的极限,最终使得二者的积是exp(-xr3/2)dt。向这个目标努力,当n很大时,将⑤代入α(r, n):
得到了这么个结果,似乎作用十分有限。再次利用⑤将会发现一个奇妙的关系:
α终于和微分扯上关系了,n很大时,它将成为⑥中的dx。
现在来看β(n, r)。为了便于操作,我们取对数以便消除幂:
既然n是一个充分大的数,那么可以判定xr/√n < 1。通过无穷级数的知识,我们知道当|x| < 1时ln(1+x)的展开式(来源可参考 单变量微积分30——幂级数和泰勒级数),并利用这一点展开lnβ:
当n充分大时,|t|< < 1, t的幂次越高,对结果的影响越小,因此我们抛弃高于t2的项,并再次借助⑤:
现在终于达到了目的:
虽然这只是一个二项分布的特殊情况,但仍然呈现出清晰的道理:任何大量独立同分布的随机过程都将以一个正态分布为模型,这也是很多分布的曲线都是倒钟形的原因。
出处:微信公众号 "我是8位的"
本文以学习、研究和分享为主,如需转载,请联系本人,标明作者和出处,非商业用途!
扫描二维码关注作者公众号“我是8位的”
![]()