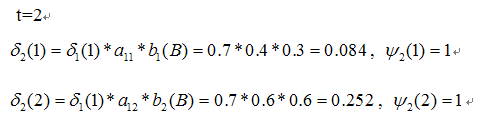HMM--hidden markov model
Hmm讲解
隐马尔科夫模型是指我现在有一个状态序列，每个状态对应一个观测量，我现在只知道每个时刻的观测量，我想知道这个状态序列最可能是什么。
举个例子，假如有三种天气，晴，雨，云；有一个人会逛街，郊游，或者在家。我现在知道他这几天的行为(观测值)是逛街，逛街，在家，郊游，我想知道这几天最可能的天气(状态)。这就是HMM解决的问题。
直观上来说,我们很容易想到：
1. 一个人显然在雨天郊游的概率小于雨天在家的概率
2. 我们也知道天气的变化遵从一定的规律，比如晴天变成晴天的概率是0.5，变成雨天的概率是0.2，变成多云的概率是0.3。
3. 另外，显然这个天气的状态序列是和第一天的天气状态有关的。
我们现在这就让我们想到，我们需要三种概率分布来描述现在这个天气--行为的模型
1. 每个天气状态下行为观察值的概率分布
2. 状态转移概率分布
3. 初始状态概率分布
HMM的数学描述
前提
HMM是基于这样的前提
1. 一个状态只由它的前一个状态确定，例如，明天天气的概率分布完全被今天的天气确定。
2. 一个状态可以完全确定观测值的概率，例如，我的行为的概率分布完全由当天的天气确定
需要值得一提的是，一个状态只由它的前一个状态确定并不是说前两个，前三个状态对当前状态没有影响，只是把这种影响通过概率的方式加到前一个状态上了。
如果一个模型满足这样的前提，那么我们可以用HMM解决其中的问题
数学推导及结论
HMM的数学推导用到的知识我们在高中的时候都学过了，但是需要大家仔细理解，在这里提醒大家，在看公式推导的时候要注意什么。
1. 这个公式的条件是什么
2. 描述的是什么物理模型
3. 自己举出例子来解释这个公式
如果学过动态规划，那么你会发现HMM包含的三个核心算法中有两个都是DP的问题(前向后向算法和Viterbi算法)。但是我觉得它的状态的定义和状态转移方程还是很巧妙的，值得学习。至于第三个Baum-Welch算法，我个人认为就是EM思想在HMM中的运用。如果有兴趣的同学可以参见我的讲解EM的博文
以下是我从南京邮电大学陈泉金学长的硕士论文中关于HMM公式部分的截图，写的很详细
Viterbi算法解决模型评估问题
给定观测序列 O=O1O2O3…Ot和模型参数λ=(A,B,π)，怎样寻找满足这种观察序列意义上最优的隐含状态序列S，这一步中最常用的算法就是Viterbi算法了。
同样的，我们先引入3个符号：
：表示在观察时刻t正处在状态j，且沿一条路径q1q2q3..qt，产生出的o1o2o3…ot最大概率。
：表示的是一个状态值，该状态值产生了上面的 ，也就是说计算时是由上一次那个状态产生的。
：表示在观察时刻t中所有的内最大的那个状态，所以它也是一个状态值。
由上面的解释可以得出这3个符合的数学表达式如下：
所有说当已知观察序列，要用viterbi算法求解最优状态序列时与前面一讲中的求最大观察值概率的算法非常相似。只是在求 时不再是将其来源相加，而是取其中最大的那个。
废话少说，还是看刚开始的那个题目：
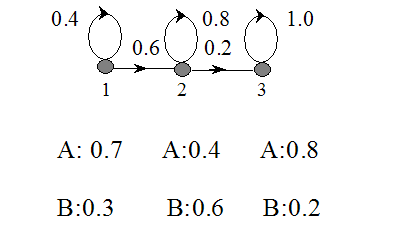
HMM模型如下，试通过前向算法计算产生观察符号序列O={ABAB}时用Viterbi算法求出最大可能的状态序列。
当然初始概率矩阵π=(1,0,0),即开始处于状态1。按照上面的公式理论，我们的递推依次解出
，
以及
。解法如下：
第一次观察时：
第二次观察时：
第三次观察时：
第四次观察时：
其递推结果为：
所以最后的结果状态序列为s1、s2、s2、s2.
其计算结果示意图如下所示：
浅绿色的箭头表示最有可能的状态序列。写得比较乱，大家随便凑合着看。