序列标注模型综述

命名实体识别是序列标注的子问题，需要将元素进行定位和分类，如人名、组织名、地点、时间、质量等。命名实体识别的任务就是识别出待处理文本中三大类（实体类、时间类和数字类）、七小类（人名、机构名、地名、时间、日期、货币和百分比） 命名实体。

一般来说进行命名实体识别的方法可以分成两大类：基于规则的方法和基于统计的方法。
基于规则的方法是要人工建立实体识别规则，存在着成本高昂的缺点。
基于统计的方法一般需要语料库来进行训练，常用的方法有最大熵、CRF、HMM、神经网络等方法。

逐一介绍。

1. 必备知识点

1.1 概率图

1.1.1 概览

在统计概率图（probability graph models）中，参考宗成庆老师的书，是这样的体系结构：

在概率图模型中，数据(样本)由公式$G=(V,E)$建模表示：

• $V$表示节点，即随机变量（可以是一个token或者一个label），具体地，用$Y=(y_1,y_2,...y_n)$为随机变量建模，注意$Y$现在是代表了一批随机变量（想象对应一条sequence，包含了很多的token），$P(Y)$为这些随机变量的分布；
• $E$表示边，即概率依赖关系。后面结合HMM或CRF的graph具体解释。

1.1.2 有向图 vs 无向图

上图可以看到，贝叶斯网络（信念网络）都是有向的，马尔可夫网络无向。所以，贝叶斯网络适合为有单向依赖的数据建模，马尔可夫网络适合实体之间互相依赖的建模。具体地，他们的核心差异表现在如何求$P=(Y)$，即怎么表示 $Y=(y_1,\cdots ,y_n）$ 这个的联合概率。

1. 有向图
   对于有向图模型，这么求联合概率：
   
   举个例子，对于下面的这个有向图的随机变量：
   
   应该这样表示他们的联合概率:
   

2. 无向图
   对于无向图，一般就指马尔可夫网络。
   
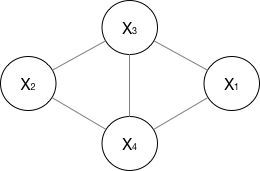
   如果一个图太大，可以用因子分解将 P=(Y) 写为若干个联合概率的乘积。将一个图分为若干个“小团”，注意每个团必须是“最大团”。则有：
   
   其中：
   
   所以像上面的无向图：
   
   其中， ${\psi }_c(Y_c)$ 是一个最大团 C 上随机变量们的联合概率，一般取指数函数的：
   
   上面的函数叫做势函数。注意 $e^{{\sum }_k{\lambda }_k{f}_k(c,y|c,x)}$ 即有CRF的影子~

   那么概率无向图的联合概率分布可以在因子分解下表示为：
   
   上述公式是CRF的开端~

1.1.3 齐次马尔可夫假设&马尔可夫性

1. 齐次马尔科夫假设
   齐次马尔科夫假设，这样假设：马尔科夫链$(x_1,x_2,...,x_n)$ 里的$x_i$总是只受$x_{i-1}$一个参数的影响。
   马尔科夫假设这里相当于就是个1-gram。

   马尔科夫过程呢？即，在一个过程中，每个状态的转移只依赖于前n个状态，并且只是个n阶的模型。最简单的马尔科夫过程是一阶的，即只依赖于其哪一个状态。

2. 马尔科夫性马尔科夫性是是保证或者判断概率图是否为概率无向图的条件。
   三点内容：a. 成对，b. 局部，c. 全局。

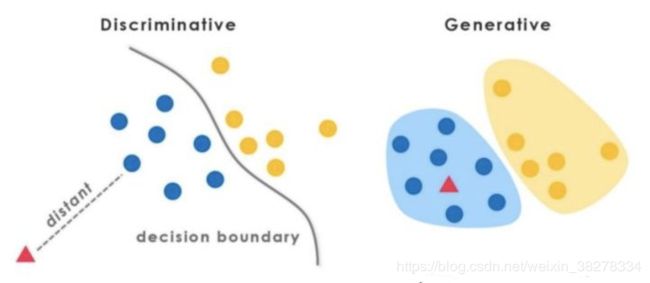
1.2 判别式（discriminative）模型 vs. 生成式(generative)模型

在监督学习下，模型可以分为判别式模型与生成式模型。
根据经验，A批模型（神经网络模型、SVM、perceptron、LR、DT……）与B批模型（NB、LDA……）的区别：

1. A批模型是这么工作的，他们直接将数据的Y（或者label），根据所提供的features，学习，最后画出了一个明显或者比较明显的边界（具体怎么做到的？通过复杂的函数映射，或者决策叠加等等mechanism），这一点线性LR、线性SVM很明显。
2. B批模型是这么工作的，他们先从训练样本数据中，将所有的数据的分布情况摸透，然后最终确定一个分布，来作为所有的输入数据的分布，并且他是一个联合分布$P(X,Y)$ (注意 $X$包含所有的特征 $x_i$ ，$Y$包含所有的label)。然后来了新的样本数据（inference），通过学习来的模型的联合分布$P(X,Y)$ ，再结合新样本给的$X$，通过条件概率就能出来$Y$：
   

• 判别式模型

  A批模型对应了判别式模型。根据上面的两句话的区别，可以知道判别模型的特征了，所以有句话说：判别模型是直接对$P(Y|X)$建模，即直接根据X特征来对Y建模训练。
  具体地，训练过程是确定构件$P(Y|X)$ 模型里面“复杂映射关系”中的参数，然后再去inference一批新的sample。

  • 所以判别式模型的特征总结如下：
  1. 对 P(Y|X) 建模
  2. 对所有的样本只构建一个模型，确认总体判别边界
  3. 根据新输入数据的特征，预测最可能的label
  4. 判别式的优点是：对数据量要求没生成式的严格，速度也会快，小数据量下准确率也会好些。

• 生成式模型
  B批模型对应了生成式模型。并且需要注意的是，在模型训练中，学习到的是X与Y的联合模型$P(X,Y)$ ，也就是说，在训练阶段是只对$P(X,Y)$ 建模，需要确定维护这个联合概率分布的所有的信息参数。完了之后在inference再对新的sample计算$P(Y|X)$ ，导出$Y$ ,但这已经不属于建模阶段了。

  结合NB过一遍生成式模型的工作流程。学习阶段，建模： $P(X,Y)=P(X|Y)P(Y)$,然后 $P(Y|X)=\frac{P(X,Y)}{P(X)}$ 。另外，LDA也是这样，只是需要确定很多个概率分布，并且建模抽样都比较复杂。

  • 所以生成式总结下有如下特点：
  1. 对$P(X,Y)$ 建模
  2. 这里我们主要讲分类问题，所以是要对每个label($y_i$)都需要建模，最终选择最优概率的label为结果，所以 没有什么判别边界。（对于序列标注问题，那只需要构件一个model）
  3. 中间生成联合分布，并可生成采样数据。
  4. 生成式模型的优点在于，所包含的信息非常齐全，所以不仅可以用来输出label，还可以干其他的事情。生成式模型关注结果是如何产生的。但是生成式模型需要非常充足的数据量以保证采样到了数据本来的面目，所以速度相比之下，慢。

最后identity the picture below:

1.3 序列建模

常见的序列有如：时序数据、本文句子、语音数据等等。广义下的序列有这些特点：

• 节点之间有关联依赖性/无关联依赖性序列的
• 节点是随机的/确定的
• 序列是线性变化/非线性的……

对不同的序列有不同的问题需求，常见的序列建模方法总结有如下：

1. 拟合，预测未来节点（或走势分析）：
   a. 常规序列建模方法：AR、MA、ARMA、ARIMA
   b. 回归拟合
   c. Neural Networks

2. 判断不同序列类别，即分类问题：HMM、CRF、General Classifier（ML models、NN models）

3. 不同时序对应的状态的分析，即序列标注问题：HMM、CRF、RecurrentNNs

本文只关注在2. & 3. 类问题下的建模过程和方法。

1. 最大熵模型

2. 隐马尔可夫模型HMM

2.1理解HMM

HMM属于典型的生成式模型。对照1.2的讲解，是要从训练数据中学到数据的各种分布，这正是HMM的5要素，其中有3个就是整个数据的不同角度的概率分布：

• $Q$, 隐藏状态集$N=\{q_1,q_2,...,q_N\}$ , 隐藏节点不能随意取，只能限定取包含在隐藏状态集中的符号。 ，
• $V$, 观测集 $M=\{v_1,v_2,...v_M\}$ , 同样观测节点不能随意取，只能限定取包含在观测状态集中的符号。
• A ，状态转移概率矩阵，这是其中一个概率分布。$A=[a_{ij}{]}_{N\ast M}$ （N为隐藏状态集元素个数），其中 $a_{ij}=P(i_{t+1}=q_j|i_t=q_i)$即第i个隐状态节点在t时刻处于状态$q_i$的条件下在t+1转移到$q_j$的概率。
• B，观测概率矩阵，这个就是另一个概率分布。$B=[b_{ij}{]}_{N\ast M}$（N为隐藏状态集元素个数，M为观测集元素个数），其中$b_{ij}=P(o_t=v_k|i_t=q_j)$ 即第i个观测节点时刻t处于状态$q_j$的条件下生成观测$v_k$的概率。
• $\pi$，初始状态概率向量：$\pi =({\pi }_i)$,其中，${\pi }_i=P(i_1=q_i)$，是时刻t=1处于状态$q_i$的概率。

隐马尔科夫模型由初始状态向量$\pi$，状态转移矩阵A和观测概率矩阵B决定。。$\pi$和A决定状态序列，B决定观测序列。因此，马尔科夫模型可以用三元符号表示，即 $\lambda$=(A,B,$\pi$),A,B,$\pi$称为隐马尔科夫模型的三要素。

状态转移概率矩阵A与初始状态概率向量$\pi$确定了隐藏的马尔科夫链，生成不可观测的状态序列。
观测概率矩阵B与状态序列综合确定了如何产生观测序列。

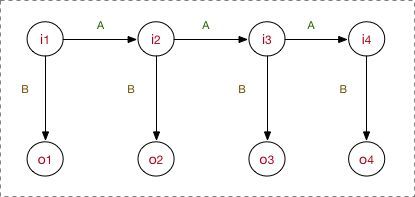
模型先去学习确定以上5要素，之后在inference阶段的工作流程是：首先，隐状态节点 $i_t$是不能直接观测到的数据节点，$o_t$才是能观测到的节点，并且注意箭头的指向表示了依赖生成条件关系，$i_t$在A的指导下生成下一个隐状态节点$i_{t+1}$，并且$i_t$ 在 B 的指导下生成依赖于该 $i_t$ 的观测节点 , 并且只能观测到序列$(o_1,o_2,...o_i)$ 。
举例子说明（序列标注问题，POS，标注集BES）：
input: “学习出一个模型，然后再预测出一条指定”
expected output: 学/B 习/E 出/S 一/B 个/E 模/B 型/E ，/S 然/B 后/E 再/E 预/B 测/E ……
其中，input里面所有的char构成的字表，形成观测集 ，因为字序列在inference阶段是我所能看见的；
标注集BES构成隐藏状态集 ，这是无法直接获取的，也是预测任务；至于A,B,$\pi$ ，这些概率分布信息都是在学习过程中所确定的参数。

高层次的理解：

1. 根据概率图分类，可以看到HMM属于有向图，并且是生成式模型，直接对联合概率分布建模:
   
   (注意，这个公式不在模型运行的任何阶段能体现出来，只是都这么来表示HMM是个生成式模型，他的联合概率 $P(O,I)$就是这么计算的)。
2. 并且B中 $b_{ij}=P(o_t|i_t)$ ，这意味着o对i有依赖性。
3. 在A中， $a_{ij}=P(i_{t+1|i_t})$，也就是说只遵循了一阶马尔科夫假设，1-gram。试想，如果数据的依赖超过1-gram，那肯定HMM肯定是考虑不进去的。这一点限制了HMM的性能。

2.2 模型运行过程

模型的运行过程（工作流程）对应了HMM的3个问题。
2.2.1 学习训练过程
对照1.2的讲解，HMM学习训练的过程，就是找出数据的分布情况，也就是模型参数的确定。
主要学习算法按照训练数据除了观测状态序列$(o_1,o_2,...o_i)$ 是否还有隐状态序列$(i_1,i_2,...i_i)$ 分为：

• 极大似然估计, with 隐状态序列
• Baum-Welch(前向后向), without 隐状态序列
  这里不展开讲~

3. 条件随机场CRF

4. Bi-LSTM+CRF

该命名实体识别方法是一种将深度学习方法和机器学习方法相结合的模型。

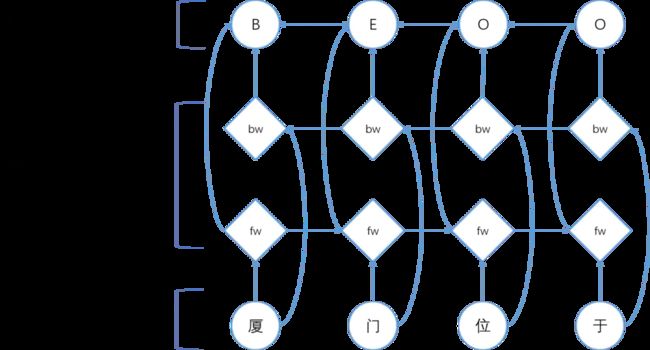
Bi-LSTM+CRF模型结构图

如图：

1. 输入层是一个将文本序列中的每个汉字利用预先训练好的字向量进行向量化，作为Bi-LSTM层的输入。
2. 利用一个双向的LSTM(Bi-LSTM)对输入序列进行encode操作，也就是进行特征提取操纵。采用双向LSTM的效果要比单向的LSTM效果好，因为双向LSTM将序列正向和逆向均进行了遍历，相较于单向LSTM可以提取到更多的特征。
3. 在经过双向LSTM层之后，我们这里使用一个CRF层进行decode，将Bi-LSTM层提取到的特征作为输入，然后利用CRF从这些特征中计算出序列中每一个元素的标签。

CRF是机器学习的方法，机器学习中困难的一点就是如何选择和构造特征。Bi-LSTM属于深度学习方法，深度学习的优势在于不需要人为的构造和选择特征，模型会根据训练语料自动的选择构造特征。因此采用Bi-LSTM进行特征的选择构造，然后采用CRF根据得到的特征进行decode，得到最终的序列标注的结果。这样讲深度学习和机器学习相结合的，互相取长补短。

参考：https://www.zhihu.com/search?type=content&q=条件随机场
https://www.zhihu.com/question/35866596/answer/236886066