K-Means牛刀小试之文档聚类

注：本文中介绍的tfidf矩阵，余弦距离计算等概念倘若有不清晰的，可以先去看看博主的前一篇文章：利用余弦距离比较文档间的相似度

一.K-Means算法的实现思路

1.1 初始化K个中心点

对于最初的k个中心结点的选取，采用的是随机选取的方式，首先是定义一个索引列表，然后根据文档的数量来生成随机数，当随机生成的索引不在索引列表中时将其添加到索引数组中去直至找齐k个中心结点的索引为止，然后利用索引去文档中找出对应的k个中心点，代码实现如下：

def randPick(k,matrix):
    """
    k：K-Means算法的k值
    matrix：文档对应的tfidf矩阵
    返回的是对应中心点
    """
    index,docnums = [],matrix.shape[0]
    random.seed(1)
    while index == [] or len(index) < k:
        idx= random.randint(0,docnums - 1)
        if idx not in index:
            index.append(idx)
    return matrix[index]

1.2 距离计算方式的选取

对于中心点与各文档间的"距离"计算公式本文采用的余弦距离，当然你也可以采取其他的距离计算方式。

1.3 K-Means的收敛方式选取

对于本项目，K-Means收敛方式有很多种：

• 指定一个固定的迭代次数
• 文档划分不再变化
• 中心点都不再发生变化

本项目最终选取的方案是：K个簇的中心点不再改变

1.4 计算文档到k个中心点的距离

对于文档到k个中心点的距离计算采用的是余弦距离，为了提升运算速度使用了numpy矩阵运算。

1.4.1 构造中心点矩阵

首先，将k个中心点构造成一个中心点矩阵，其结构如下图所示：

在中心点矩阵中，每行代表一个中心点，总行数为K表示共有K个中心点。

1.4.2 构造文档矩阵

文档矩阵即为文档的tfidf矩阵，具体介绍详解本文开头链接文章，为了方便理解后面的距离计算过程，同样将其结构展示如下：

1.4.3 中心点到各文档的距离计算

设中心点矩阵为$C$，其维度为$K\times N$，文档矩阵为$D$，其维度为$M\times N$（M为文档数），因此中心点与文档的距离计算公式如下：
$$Dis=C\bullet D^{\mathrm{T}}$$
最后计算出的距离矩阵维度为$K\times M$，其结构见下图：

由图我们可以清楚的看到，在该距离矩阵中，每一行代表了$M$个文档到该行对应的中心点的距离。

1.4.4 对应源码展示

def getCosineDistance(seeds,docmatrix):
    """
    计算中心点与各个文档间的距离
    seeds：中心点
    docmatrix：标识文档矩阵
    """
    return np.matmul(seeds,docmatrix.T)

1.5 分配文档到最近的簇并计算簇的中心点

1.5.1 分配文档到对应的簇

根据距离矩阵，我们可以找到距离每个文档最近（余弦距离值最大）的中心点，然后将其分配到对应的中心点所在的簇即可。该过程实质上就是找第$j$列的最大值所在的行$i$，因为第$j$列代表文档$j$，第$i$行代表中心点$i$，要实现该功能可以使用Numpy中的内置函数numpy.where，该函数的详细用法这里不做详细阐述。

1.5.2 簇中心的计算方式

对于划分后的簇，其中心点为簇中所有文档的"平均值"。

1.5.3 对应源码展示

def redivideClusters(cosmatrix,k,docmatrix):
    """
    cosmatrix：根据中心点计算出的余弦矩阵
    将文档划分到对应的簇，并返回新划分的簇和对应簇的中心点
    """
    clusters = [[] for _ in range(k)]   #k个簇
    x,y = np.where(cosmatrix == np.max(cosmatrix,axis=0))
    for i,j in zip(x,y):
        #print(cosmatrix[i][j])
        clusters[i].append(j)
    #重新计算中心点
    nseeds = []
    for cluster in clusters:
        vectors = docmatrix[cluster]
        s = (np.sum(vectors,axis=0) / len(vectors)).tolist()
        nseeds.append(s)
       
    return clusters,np.array(nseeds)

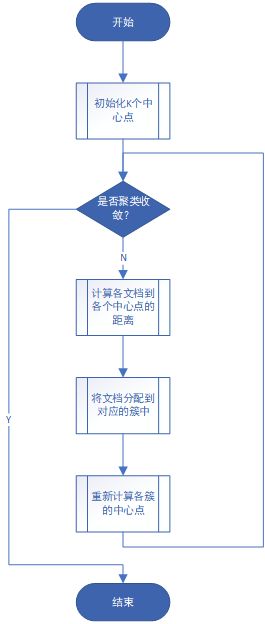
1.6 完整算法流程

1.6.1 完整算法流程图展示

1.6.2 K-Means算法主函数源码

def kmeans(k,norm):
    """
    k：簇个数
    norm：经过归一化后的文档tfidf矩阵
    输出k个簇和最终的中心点
    """
    seeds,clusters = randPick(k,norm),[] #从文档矩阵中随机挑选k个中心点
    clusterChanged = True #聚簇收敛标志位

    while clusterChanged:
        cd = getCosineDistance(seeds,norm) #计算各文档到各中心的距离
        clusters,nseeds = redivideClusters(cd,k,norm) #将各文档划分到对应的簇
        if (np.array(nseeds) == np.array(seeds)).all(): #中心不再发生变化
            clusterChanged = False
        else:
            seeds = nseeds
    return clusters,seeds

二.聚类结果展示

本项目设定的K值为20，将587个中文新闻文档进行聚簇后的最大的三个簇进行展示如下：

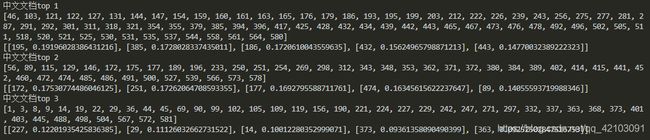
在该结果中第一个列表为簇中文档在文档列表中的索引其真实文档编号为该值加1，第二个列表中每个子元素都包含一个文档索引和其到对应中心点的距离。下面挑取其中第二个簇中距离簇中心最近的5个文档进行展示：

由上述结果可以看出五篇文章都是和全国游泳冠军赛话题有关的。

三.结语

以上便是本文的全过程，在上述过程中有些地方是可以进行改进的，例如K值的选择等，这些各位可以私下进行实践，最后还是日常求支持，你们的支持是博主码文的不竭动力！！！
完整源码下载：项目github开源地址