关于使用遗传算法解决TSP商旅问题的实例——MATLAB下的模型创建

1 遗传算法基本概念

借鉴自然进化的理念，问题优化的过程可以看成类似于生物进化的过程，通过模拟自然界的生物进化，研究者提出了一种解决优化问题的创造性方法———GA遗传算法。

1.1基本算法原理

GA算法最开始为一种随机自适应的全局搜索算法。
遗传算法正是通过模拟自然界中生物的遗传进化过程，对优化问题的最优解进行搜索。算法维护一个代表问题潜在解的群体，对于群体的优化，算法引入了类似自然进化中选择、交配、以及变异算子。遗传算法搜索全局最优解的过程是一个不断迭代的过程，每一次迭代相当于生物进化中的一次循环，直到满足算法的终止条件为止。

在遗传算法中，问题的每个有效解被称为一个“染色体”，在有些书籍中也称为“串”，相对于群体中每个生物个体，染色体的具体形式是一个使用特定编码方式生成的串，编码串中的每一个编码单元称为基因。

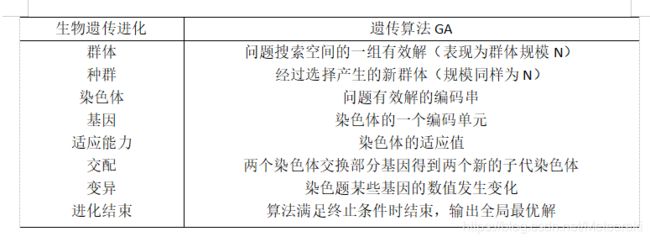
1.2 比较对应

1.3理论支持

①模式定理

对于遗传算法，Holland给出了著名的模式定理，为遗传算法提供了理论支持。

模式： 是指群体中编码的某些位置具有相似结构的染色体集合。这边可用0或1组成的二进制符号序列作为染色体的编码。其中如：
模式01 x x x 0 则表示以01开头且0结尾的编码串对应的染色体的集合。

阶： 模式中具有确定取值的基因个数，如0 1 x x x 0 的阶为3。

模式定义长度： 是指模式中第一个具有确定取指的基因到最后一个具有确定取值的基因的距离，上例为5。 而x 1 x x x x 定义长度为0.

该定理指出，遗传算法的实质是通过选择、交配、变异算子对模式进行搜索，缔结定义长度较小且平均适应高于群体平均适应值的模式在群体中方的比例将呈现指数级增长，即随着精华的不断进行，教优染色体个数将快速增加。模式定理证明了遗传算法寻求全局最优解的可能性，但是不能抱枕算法一定能找到全局最优解，Goldberg提出的积木块假设，能对该定理做出补充，说明遗传算法具有能找到全局最优解的能力。

2 具体算法流程

遗传算法的实现主要包含以下七个重要问题：

1. 染色体的编码；
2. 躯体的初始化；
3. 适应值评价；
4. 选择种族；
5. 种族交配；
6. 群体变异；
7. 算法流程；

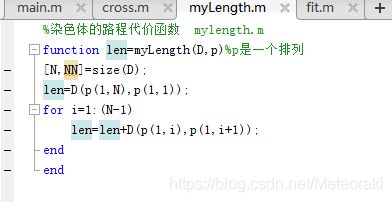
2.1 染色体的编码

目前用于染色体编码的方式有格雷码编码，字母编码，多参数交叉编码。这里我们采用两种较为简单的编码：二进制编码和浮点数（实数）编码。其中二进制编码较为简单，但是在编码精度方面较差，史书编码方式适合于表示取值范围比较大的数值，用于多维函数优化问题，效果较为突出，对降低采用遗传算法对染色体进行处理的复杂性起到了很好的作用。

2.2 群体初始化

遗传算法在一个给定的初始进化群体进行迭代搜索，一般情况下遗传算法在躯体初始化阶段采用的是随机数初始方法的。

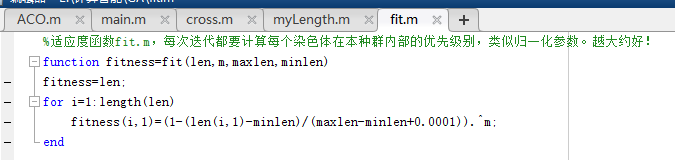
2.3 适应值评价

评估函数用于评估各个染色体的适应值，进而区分优劣。具体问题时，可以套用问题定义的函数表达式。例如求解某个函数的最小值可以对问题定义的目标函数F（x）进行以下变化得到算法的评估函数Eval（C）。

                         Eval（c）= -f（x）
                其中x表示一个有效解，c表示x对应的染色体

适应值会出现两种情况，一种时极小情形即院十适应值越小个体性能越好，另一种反之。
遗传算法中某些选择策略则要求适应函数时非负的，而且适应值越大表明个体的性能越好。

2.4选择算子

种群的选择使用轮盘赌选择算法该算法是遗传算法最经常使用的选择算法，基本思想是给予概率的随机选择。不同的选择策略将 导致不同的选择压力，即下一代附带个体的复制数目的不同分配关系。

轮盘赌选择算法
首先根据群体中每个染色体的适应值得到群体中所有染色体的适应值综合，并且分别计算每个染色体适应值于群体适应值总和的比Pi即所占总体的百分比，将一个圆盘分为若干份，对应成正比关系。
每次转动轮盘表示一次选择，，依次进行N次选择即可得到规模同样为N的种群。
以下为轮盘转动的伪代码:

FUNCTION RWS
  M->0;
  R->random(0,1);
  for i=0 to N
  M->M+Pi;
  if R<=M
    return i;
    end if
    end for
    end FUNCTION

从以上机制可以看出，较优染色体的P值较大，被选择的概率就相对较大，但是由于选择过程具有随机性，不能每次都选中较优染色体，因此给予了较差染色体的生存空间。

2.5 交配算子(杂交算子)

杂交运算是指对两个相互匹配的染色体按某种方式相互交换其部分基因而形成两个新的个体。
① 单点杂交：称为简单杂交，它指在个体编码串中值随机设计一个杂交点，然后再该店互换两个配对个体的部分染色体。

 如下：
 0110 1              0110 0
           ————>
 1100 1              1100 1

②双点杂交与多点杂交
双点杂交是指再个体编码串中设置了两个杂交点，然后再进行基因交换。

③均匀杂交
均匀杂交是指两个配对个体每一个基因座上的基因都以相同的杂交概率进行交换，从而形成两个新的个体。均匀杂交实际上可归属多点杂交的范围。

2.6 变异算子

染色体的变异作用于基因上，对于交配后新中去中染色体的每一位基因根据变异概率Pm判断该基因是否进行变异。实际运用中可适当降低变异率，目的是为了保持遗传算法较好的运行性能。一般设置在0.001~0.1之间。遗传算法中使用变异算子主要偶以下两个目的：
1）改善遗传算法的局部搜索能力。
2）维持群体的多样性，防止出现早熟现象。

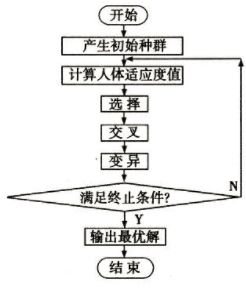
2.7 算法流程

1. 初始化规模为N的群体，其中染色体每个基因的值采用随机数产生器生成并满足问题定义的范围，当前进化代数Generation为0。
2. 采用评估函数对群体中所有染色体进行评价，分别计算每个染色体的适应值，保存适应值最大的染色体Betst。
3. 采用轮盘赌选择算法对群体的染色体进行选择操作产生规模同样的为N的种群。
4. 按照概率Pc从种群中选择染色体进行交配，每两个进行交配的附带染色体，交换部分基因产生两个新的子代染色体，子代染色体取代父代染色体进入新种群。没有进行交配的染色体直接复制进入新的种群。
5. 按照概率Pm对新种群中染色体的基因进行变异操作，发生变异基因数值发生改变。变异后的染色体取代原有染色体进入新群体，未发生变异的染色体直接进入新群体。
6. 变异后的新群体取代原有群体，重新计算群体中各个染色体的适应值，倘若群体的最大适应值大于Best的适应值，则以该最大适应值对应染色体替代Best。
7. 当前进化代数Generation加1，如果Generation超过规定的最大进化代数或B二十天达到规定的误差要求，算法结束 否则返回第三步。

3 关于经典TSP问题

在求解这个问题前，我们先来回顾以下tsp问题的定义。旅行商问题，即TSP问题(Travelling Salesman Problem)又译为旅行推销员问题、货郎担问题，是数学领域中著名问题之一。假设有一个旅行商人要拜访n个城市，他必须选择所要走的路径，路径的限制是每个城市只能拜访一次，而且最后要回到原来出发的城市。路径的选择目标是要求得的路径路程为所有路径之中的最小值。

4 解决问题的分析

那么我们之前有通过遗传算法的参数设置来知道遗传迭代的过程，也通过蚁群算法来解决TSP问题，那么如何用遗传的迭代来求解TSP问题呢？如下分析：
我们将通过修改城市序列，种群数目和交叉变异概率来测试该模型在不同情况下的运行情况，在不断训练中学习参数和原理。

4.1第一次原始测试

具体步骤如下：

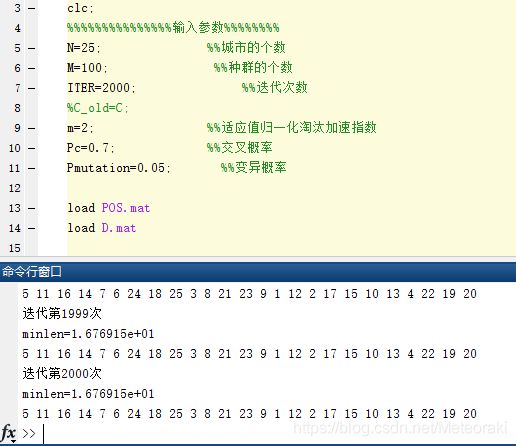
①参数设置

之后的调试训练代码和这些参数有关。

②生成基础城市地图

为了保证实验结果参数变量的唯一性，我们最开始通过随机生成城市地图来找到合适的位置，最终确定下地图，用load函数方法将其中一个随机生成的地图导入。

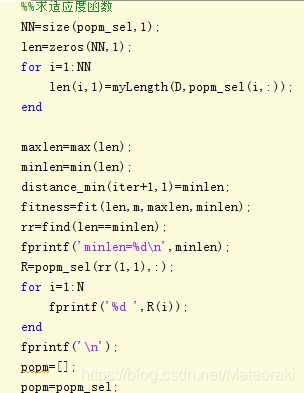
③ 选择算子匹配自适应函数

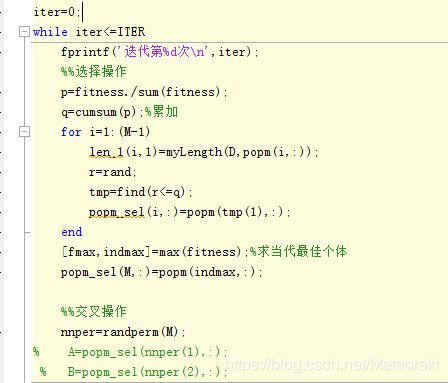
④开始迭代

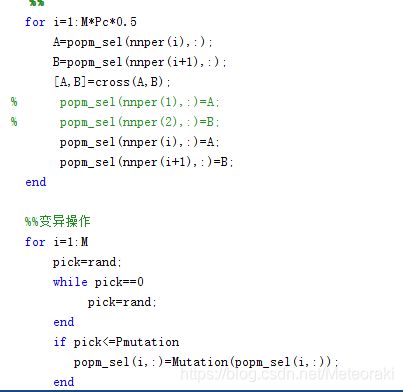
每次迭代后都需要进行交叉操作和变异操作

同时在迭代中求自适应函数（每次都不同）

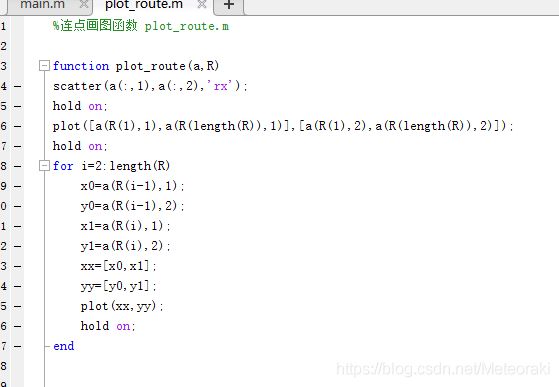
⑤结束迭代可视化结果

⑥实验结果展示

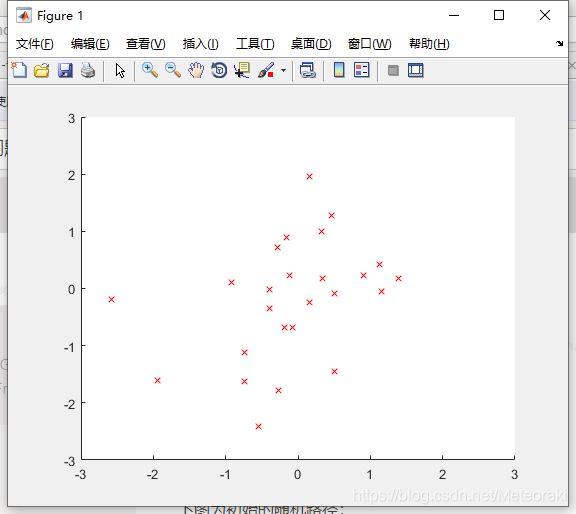
下图figure1为随机生成的城市地图：

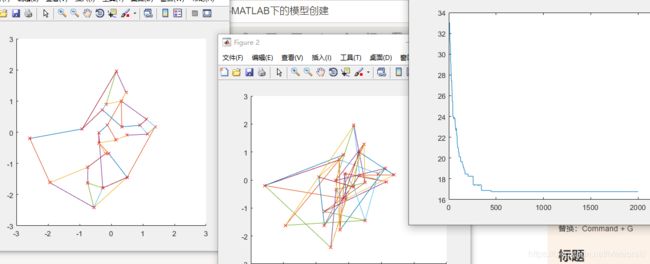
下图figure2为初始的随机路径：

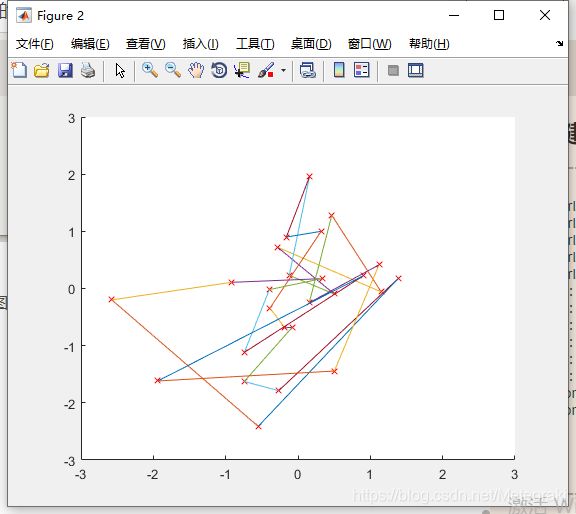
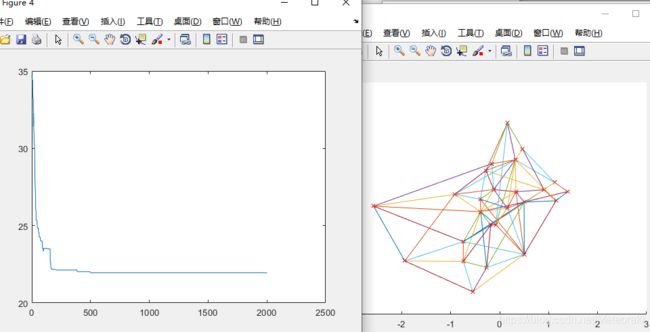
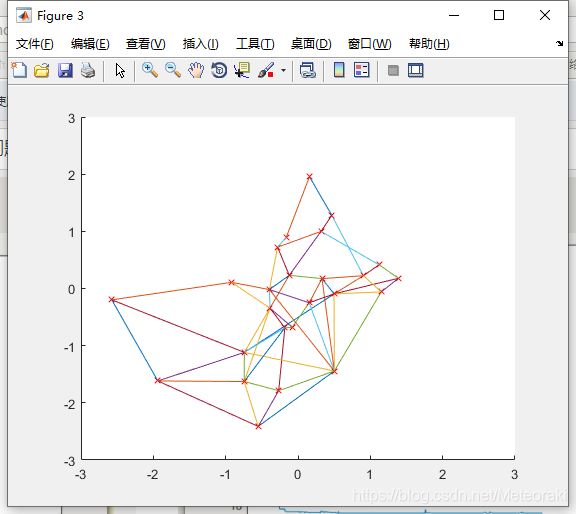
下图figure3为最终迭代后确定的最短路径：

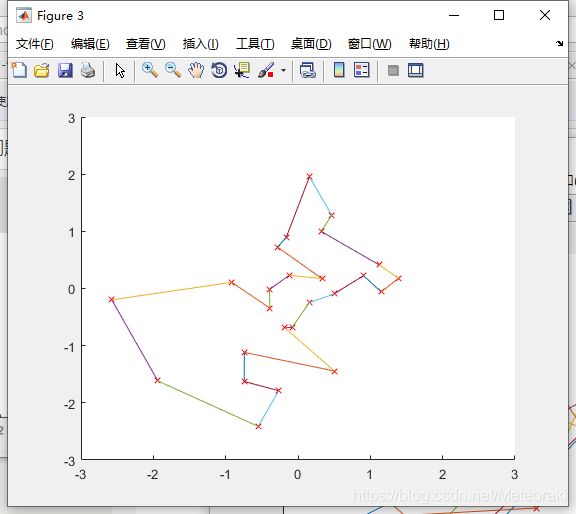
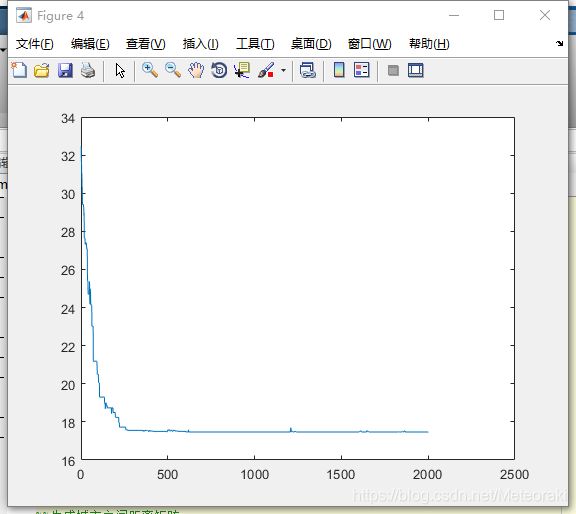
下图figure4为迭代最短路径的变化曲线：

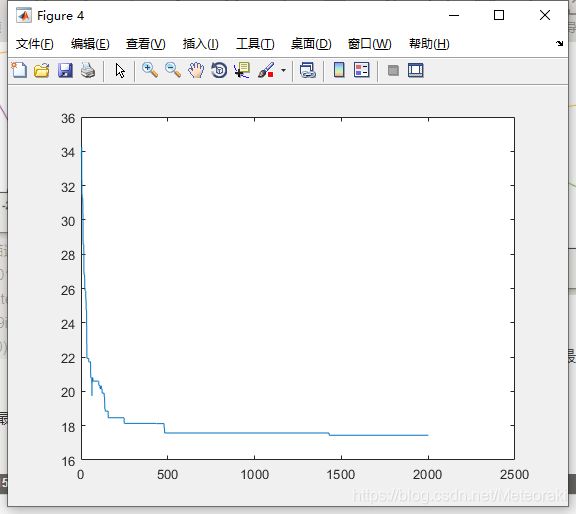
可以看出，随着迭代次数的不断增加，最短路径越来越小且变化逐渐趋于平缓。

4.2修改参数再测试

最初的原始参数为：

将种群的个数修改为500：

测试结果：


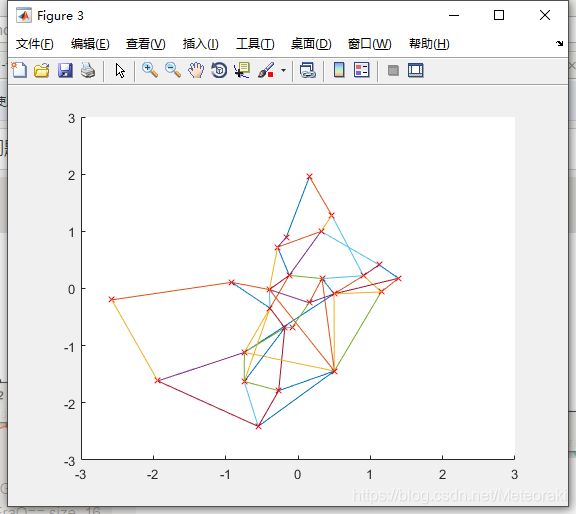
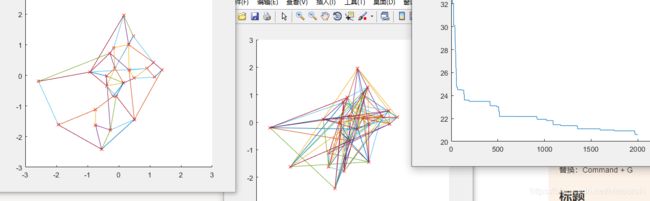
当我把种群数量改为3000时，迭代时间大大加长：

适应值归一化淘汰加速指数不宜过大！多次测试结果浮动极大！
这里将m从2改为5

改小交叉概率，由原来的0.8改为0.5，不得变太小，否则很难通过现有次数的迭代找到最小值，不宜过大，否则也找不到最佳（改为0.9后效率没有明显提高，且有所下降）0.7的效果比0.8的好！！！！！

将变异概率从0.05修改到0.1
看看结果如何：（这个结果以外的也很不错！）

当变为0.01时呢！
这时我们发现，他的迭代效果非常差，到很后面的还在发生大的下滑，所以变异太小也不可取！

5 结论

交叉概率需要适中，不宜过大不宜过小，变异概率同理，种群数量不是越多越好，根据网路上的解释又看到说3000为佳，我就测试了，感觉效果蛮一般的，我又测试了4000感觉效果也没啥特别突出越到迭代后期会出现震荡，归一化加速值不宜随便调整！