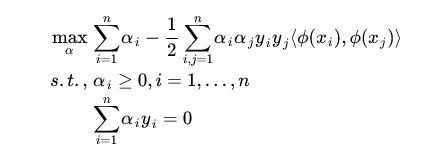Spark机器学习系列之13： 支持向量机SVM

支持向量机系列学习笔记包括以下几篇：
Spark机器学习系列之13： 支持向量机SVM ：http://blog.csdn.net/qq_34531825/article/details/52881804
支持向量机学习之2：核函数http://blog.csdn.net/qq_34531825/article/details/52895621
支持向量机学习之3：SVR（回归）http://blog.csdn.net/qq_34531825/article/details/52891780

C−SVM 基本公式推导过程

理论部分：SVM涉及的理论知识非常繁杂了，大家直接看：
支持向量机通俗导论（理解SVM的三层境界） http://blog.csdn.net/v_july_v/article/details/7624837

下面摘抄一小部分内容（不考虑推导细节的话，基本上能理解C-SVM方法推导的整个流程）.

对偶问题（包括KKT条件）在SVM起到很重要的作用，如果对此不很了解，则难以理解SVM推导过程。关于对偶分析，可以参考我的另一篇文章:http://blog.csdn.net/qq_34531825/article/details/52872819) 。

核函数部分可以参考http://blog.csdn.net/qq_34531825/article/details/52895621。

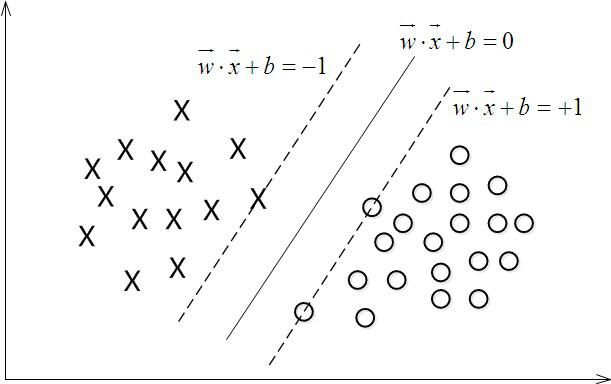
我们用一个超平面划分图中对图中的两类数据进行分类，超平面写成 f(x)=wTx+b=0 ,在线性可分的情况下，我们能找到一些支持向量，满足 |wTx+b|=1 。

如何理解这一点呢？如果我们找到一个 （w，b） 来表达超平面 f(x)=wTx+b=0 ,那么通过缩放，相当于找到了无数个 （λ∗w，λ∗b）,λ不等于0即可 ，都可以等价的来表达这个超平面，比如说 f(x)=3x1+4x2−2x3+6=0 和 f(x)=1.5x1+2x2−x3+3=0 表示一模一样的超平面，也就是说我们通过缩放(w,b)，总能使得里超平面两侧最近的距离相等的这些支持向量(support vectors)满足 |f(xi)|=|wTxi+b|=1 ，以达到简化问题的目的。

对一个数据点进行分类，当超平面离数据点的“间隔”越大，分类的确信度（confidence）也越大。所以，为了使得分类的确信度尽量高，需要让所选择的超平面能够最大化这个“间隔”值。这个间隔如下图中的 Gap2 所示。

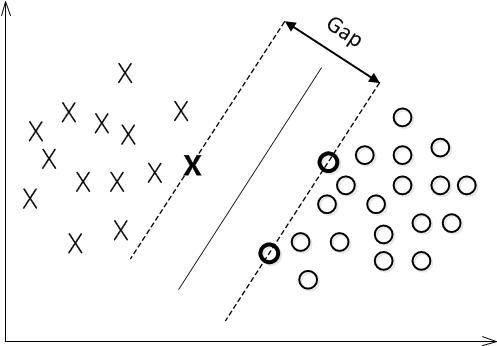
从解析几何的角度可以证明 xi 点离超平面方程 wTx+b=0 的距离为：

γ=|wTxi+b|||w||=|f(xi)|||w||

由于支持向量满足 |wTxi+b|=1 ,因此 Gap2=1||w||
定义函数
yi=1      当f(x)>0,
yi=−1   当f(x)<0,

需要求解的目标函数及约束条件为：

max  1||w||

s.t.   yi(wTxi+b)≥1   i=1,2...n

等价于下面的凸二次规划问题：

min  12||w||2

s.t.   yi(wTxi+b)≥1   i=1,2...n

可以利用通过拉格朗日对偶性（Lagrange Duality）变换到对偶变量 (dual variable) 的优化问题。（关于对偶分析，可以参考我的另一篇文章:http://blog.csdn.net/qq_34531825/article/details/52872819) 。

拉格朗日函数为：

L(w,b,α)=12||w||2−∑i=1nαi(yi(wTxi+b)−1)

原问题的对偶函数为：

θ(w,b,α)=maxαi≥0{L(w,b,α)}

对偶问题为：

min  θ((w,b,α))

αi≥0

按照KKT条件求解：
首先对w和b求偏导：

∂L∂w=0=>w=∑i=1nαiyixi

∂L∂b=0=>∑i=1nαiyi=0

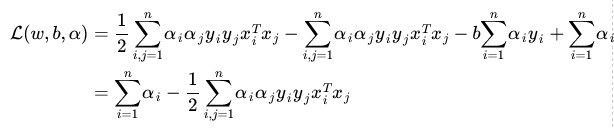
问题转换为下公式，只包含变量 α

对于非线性数据，用核函数进行映射 xi↦ϕ(xi),xj↦ϕ(xj) ：

使用松弛变量处理 outliers 方法
虽然通过映射 将原始数据映射到高维空间之后，能够线性分隔的概率大大增加，但是对于某些情况还是很难处理。

例如可能并不是因为数据本身是非线性结构的，而只是因为数据有噪音。对于这种偏离正常位置很远的数据点，我们称之为 outlier ，在我们原来的 SVM 模型里，outlier 的存在有可能造成很大的影响，因为超平面本身就是只有少数几个 support vector 组成的，如果这些 support vector 里又存在 outlier 的话，其影响就很大了。

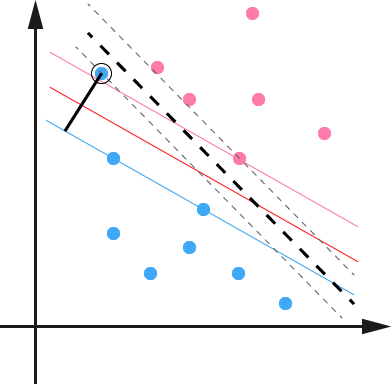
现在考虑到outlier问题，引入松弛变量：

原问题变成

其中 C 是一个参数，用于控制目标函数中两项（“寻找 margin 最大的超平面”和“保证数据点偏差量最小”）之间的权重。 C 是一个事先确定好的常量。
对偶问题：

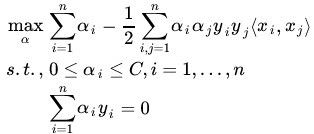
序列最小最优化SMO算法：
在 α={α1,α2,...,αn} 上求上述目标函数的最小值。为了求解这些乘子，每次从中任意抽取两个乘子 α1,α2 ，然后固定 α1,α2 以外的其它乘子 α3,α4,...,αn ，使得目标函数只是关于 α1,α2 的函数。这样，不断的从一堆乘子中任意抽取两个求解，不断的迭代求解子问题，最终达到求解原问题的目的。

以上内容主要摘抄自：
支持向量机通俗导论（理解SVM的三层境界） http://blog.csdn.net/v_july_v/article/details/7624837
希望了解全面SVM，推荐参考原文。

Spark 优缺点分析

以下翻译自Scikit。
The advantages of support vector machines are:
（1）Effective in high dimensional spaces.在高维空间表现良好。
（2）Still effective in cases where number of dimensions is greater than the number of samples.在数据维度大于样本点数时候，依然可以起作用
（3）Uses a subset of training points in the decision function (called support vectors), so it is also memory efficient.仅仅使用训练数据的一个子集（支持向量），因此是内存友好型的算法。
（4）Versatile: different Kernel functions can be specified for the decision function. Common kernels are provided, but it is also possible to specify custom kernels.适应广，能解决多种情况下的分类问题，这是由于它支持不同类型的核函数，甚至支持自定义的核函数。
能灵活使用多种核函数的确使得SVM变得非常强大，而核函数相关的理论很深奥，初步的探讨可参考转载的一篇文章：http://blog.csdn.net/qq_34531825/article/details/52895621
The disadvantages of support vector machines include:
（1）If the number of features is much greater than the number of samples, the method is likely to give poor performances.在数据维度（特征个数）多于样本数很多的时候，通常只能训练出一个表现很差的模型。
（2）SVMs do not directly provide probability estimates, these are calculated using an expensive five-fold cross-validation (see Scores and probabilities, below).SVM不支持直接进行概率估计，Scikit中使用很耗费资源的5折交叉检验来估计概率。

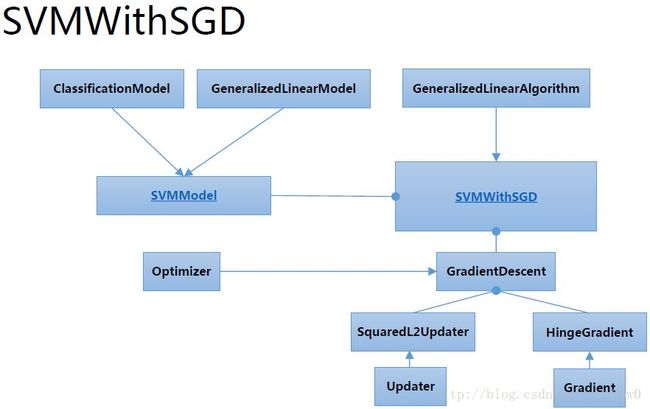
Spark Mllib

import org.apache.spark.{SparkConf,SparkContext}
import org.apache.log4j.{Level, Logger}
import org.apache.spark.mllib.classification.{SVMModel,SVMWithSGD}
import org.apache.spark.mllib.evaluation.BinaryClassificationMetrics
import org.apache.spark.mllib.util.MLUtils
import org.apache.spark.SparkConf
import org.apache.spark.SparkContext
import org.apache.spark.mllib.optimization.L1Updater
import org.apache.spark.mllib.optimization.SquaredL2Updater

object mySVM {
  def main(args:Array[String]){
    //屏蔽日志
    Logger.getLogger("org.apache.spark").setLevel(Level.ERROR)
    Logger.getLogger("org.eclipse.jetty.server").setLevel(Level.OFF) 
    val conf=new SparkConf().setMaster("local").setAppName("My App")
    val sc=new SparkContext(conf)

    // Load training data in LIBSVM format.
    val data = MLUtils.loadLibSVMFile(sc, "/data/mllib/sample_libsvm_data.txt")
    //println(data.collect()(0))//检查数据   

    // Split data into training (60%) and test (40%).
    val splits = data.randomSplit(Array(0.6, 0.4), seed = 11L)
    val training = splits(0).cache()
    val test = splits(1)

    // Run training algorithm to build the model   
    /*
     * stepSize: 迭代步长，默认为1.0
     * numIterations: 迭代次数，默认为100
     * regParam: 正则化参数，默认值为0.0
     * miniBatchFraction: 每次迭代参与计算的样本比例，默认为1.0
     * gradient：HingeGradient ()，梯度下降；
     * updater：SquaredL2Updater ()，正则化，L2范数；
     * optimizer：GradientDescent (gradient, updater)，梯度下降最优化计算。
     */
    val svmAlg=new SVMWithSGD()
    svmAlg.optimizer
      .setNumIterations(100)
      .setRegParam(0.1)//正则化参数
      .setUpdater(new L1Updater)
    val modelL1=svmAlg.run(training)


    // Clear the default threshold.
    modelL1.clearThreshold()

   // Compute raw scores on the test set.
    val scoreAndLabels = test.map { point =>
     val score = modelL1.predict(point.features)     
     (score, point.label)//return score and label
    }   

   // Get evaluation metrics.
   val metrics = new BinaryClassificationMetrics(scoreAndLabels)
   val auROC = metrics.areaUnderROC() 
   println("Area under ROC = " + auROC)  

  }   

}

Python Scikit

Scikit-learn对于SVM提供更多灵活的选择，可供学习实验。

处理数据不平衡问题

数据不平衡问题虽然不是最难的，但绝对是最重要的问题之一。

很多算法都有一个基本假设，那就是数据分布是均匀的。当我们把这些算法直接应用于实际数据时，大多数情况下都无法取得理想的结果。因为实际数据往往分布得很不均匀，都会存在“长尾现象”，也就是所谓的“二八原理”。(摘自文献6）

不平衡数据的场景也出现在互联网应用的方方面面，如搜索引擎的点击预测（点击的网页往往占据很小的比例），电子商务领域的商品推荐（推荐的商品被购买的比例很低），信用卡欺诈检测，网络攻击识别等等。（文献7）

处理方法通常有采样，加权，合成和一分类等方法（文献6）

SVM采用加权的办法来处理数据不平衡问题。（文献4）

（1）SVC (不包括NuSVC)，使用关键词 class_weight（大于0），对某类样本进行加权。内部将C值重设为C *class_weight。
（2）SVC, NuSVC, SVR, NuSVR and OneClassSVM ，使用关键词sample_weight对单独各个样本进行加权，内部对第i个样本C值重设为C×sample_weight[i]

（1）SVC (but not NuSVC) implement a keyword class_weight in the fit method. It’s a dictionary of the form {class_label : value}, where value is a floating point number > 0 that sets the parameter C of class class_label to C * value.
（2）SVC, NuSVC, SVR, NuSVR and OneClassSVM implement also weights for individual samples in method fit through keyword sample_weight. Similar to class_weight, these set the parameter C for the i-th example to C * sample_weight[i].

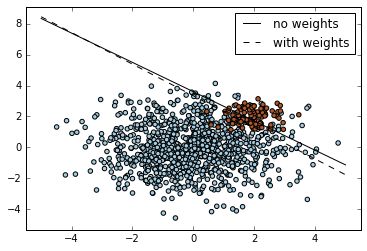
下图是Scikit 处理不平衡数据的一个简单例子：

其关键代码如下：

#假设第0类有1000个点，第1类有100个点，那么采用下面两种方式，都能获得一样
#的结果。对第1类乘以10，或者对第0类乘以0.1,就达到了均衡两类数据点数目的目的。
#对第1类C×10
wclf = svm.SVC(kernel='linear', C=1.0,class_weight={1: 10})
#或者对第0类C×0.1
wclf = svm.SVC(kernel='linear', C=1.0,class_weight={0:0.1})
#然后fit
wclf.fit(X, y)

如下按照

#第1类样本数是第0类数样本2倍
wclf = svm.SVC(kernel='linear', C=1.0,class_weight={1: 5})
#可以看到有6% 红点（0类）被错分

#第1类样本数是第0类数样本5倍
#可以看到有大量红点被错分，尽量对于总体（红点+蓝点）而言，正确率还是很高，
#但是对于我们关心的红点而言，却是不能接受的结果，因此数据不平衡问题一定要
#处理到位。
wclf = svm.SVC(kernel='linear', C=1.0,class_weight={1: 2})

完整代码请看Scikit example：http://scikit-learn.org/stable/auto_examples/svm/plot_separating_hyperplane_unbalanced.html#sphx-glr-auto-examples-svm-plot-separating-hyperplane-unbalanced-py

测试参数

Scikit中可选择的参数：
（1）C : 浮点型，可选 (默认=1.0)。误差项的惩罚参数C
（2）kernel : 字符型, 可选 (默认=’rbf’)。指定核函数类型。只能是’linear’, ‘poly’, ‘rbf’, ‘sigmoid’, ‘precomputed’ 或者自定义的。如果没有指定，默认使用’rbf’。如果使用自定义的核函数，需要预先计算核矩阵。
（3）degree : 整型 可选 (默认=3)。用多项式核函数(‘poly’)时，多项式核函数的次数(单项式的幂），用其他核函数，这个参数可忽略。
（4）gamma : 浮点型, 可选 (默认=0.0)。’rbf’, ‘poly’ and ‘sigmoid’核函数的系数。如果gamma是0，实际将使用特征维度的倒数值进行运算。也就是说，如果特征是100个维度，实际的gamma是1/100。
（5）coef0 : 浮点型, 可选 (默认=0.0)。核函数的独立项，’poly’ 和’sigmoid’核时才有意义。
高斯核函数（rbf）
由于这个函数类似于高斯分布，因此称为高斯核函数，也叫做径向基函数(Radial Basis Function 简称rbf)。

exp(−γ|x−x′|2),γ>0

机器学习大牛Andrew Ng说，关于SVM分类算法，他一直用的是高斯核函数，其它核函数他基本就没用过。可见，这个核函数应用最广。

∙ gamma参数，当使用高斯核进行映射时，如果选得很小的话，高次特征上的权重实际上衰减得非常快，所以实际上（数值上近似一下）相当于一个低维的子空间；反过来，如果gamma选得很大，则可以将任意的数据映射为线性可分——这样容易导致非常严重的过拟合问题[文献9]。
gamma控制函数径向作用的范围，也就是单个训练样本能够影响的范围，值越小表明影响越远。

Intuitively, the gamma parameter defines how far the influence of a single training example reaches, with low values meaning ‘far’ and high values meaning ‘close’. The gamma parameters can be seen as the inverse of the radius of influence of samples selected by the model as support vectors.

∙ C参数是寻找 margin 最大的超平面”和“保证数据点偏差量最小”）之间的权重。C越大，模型允许的偏差越小。

具体问题时需要对上述两个参数不同组合进行测试分析，上述两个参数实际上是在模型在训练集上的分类准确性与模型泛化能力（过拟合）之间作斗争，我个人觉得实际上是与其它机器学习中的正则化参数可以起到类似的作用。

下图来自文献11（官网例子）
http://scikit-learn.org/stable/auto_examples/svm/plot_rbf_parameters.html

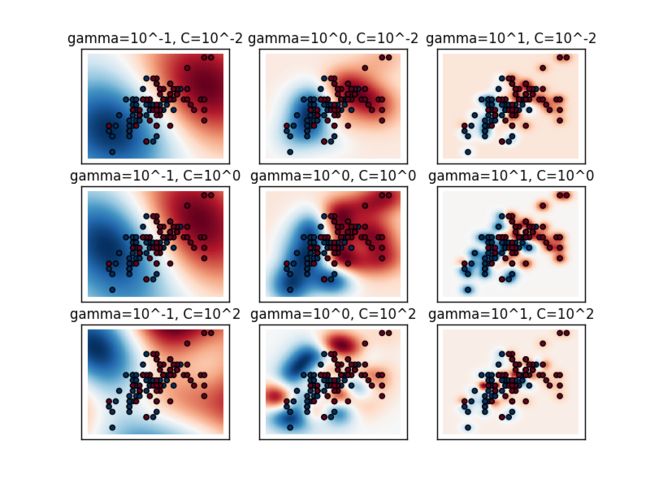
说明：gamma控制函数径向作用的范围，也就是单个训练样本能够影响的范围，值越小表明影响越远，值越大表明影响越近。

说明：需要合适的C 和gamma参数组合，才能获得较好的分类效果（分类准确，且模型泛化能力强）。

参考文献
（1） 支持向量机通俗导论（理解SVM的三层境界） http://blog.csdn.net/v_july_v/article/details/7624837
（2）Spark MLlib SVM算法（源代码分析）http://www.itnose.net/detail/6267193.html
（3）Spark官网与Scikit官网
（4）LIBSVM: A Library是 for Support Vector Machines , Chih-Chung Chang and Chih-Jen Lin，Department of Computer Science National Taiwan University, Taipei, Taiwan http://www.csie.ntu.edu.tw/~cjlin/papers/libsvm.pdf
（5）A Tutorial on Support Vector Regression Alex J. Smola† and Bernhard Scholkopf
（6）如何解决机器学习中数据不平衡问题 http://www.zhaokv.com/2016/01/learning-from-imbalanced-data.html
（7）不平衡数据下的机器学习方法简介 http://www.jianshu.com/p/3e8b9f2764c8
（8）核函数 http://blog.csdn.net/xiaojiegege123456/article/details/7728198，xiaojiegege123456 CSDN 对核函数有一个比较容易的理解的介绍
（9）http://www.cnblogs.com/zxb1990/p/5098345.html SVM学习笔记（二）—-手写数字识别 贴近实际应用一些
（10）http://www.cnblogs.com/jerrylead/archive/2011/03/18/1988406.html
（11）RBF 参数 http://scikit-learn.org/stable/auto_examples/svm/plot_rbf_parameters.html