SMO算法详细推导(Sequential Minimal Optimization)
本文针对一般性的“软判断的核函数的对偶问题的SVM”,形如下式:

上式问题所在:当采样点 x i x_i xi 选取50000个点时,则基于核函数变量 Θ ( x i , x j ) \bm{\Theta(x_i,x_j)} Θ(xi,xj)将需要大约10GB的RAM来存储 Θ ( x i , x j ) \bm{\Theta(x_i,x_j)} Θ(xi,xj)。这里介绍前人所提的SMO算法,以降低存储空间。
一. 算法流程框架
首先,先给出SMO算法的算法流程,如下:

意思是:第一步,选取一对 α i \alpha_i αi和 α j \alpha_j αj,选取方法使用启发式方法。第二步,固定除 α i \alpha_i αi和 α j \alpha_j αj之外的其他参数,确定目标函数(即: W ( α ) W(\alpha) W(α)。图片中用 W ( α ) W(\alpha) W(α)表示整个目标函数)取得最大值时的 α i ∗ \alpha_i^* αi∗的取值,并由 α i ∗ \alpha_i^* αi∗计算出 α j ∗ \alpha_j^* αj∗。重复迭代上述两步,直到收敛。
SMO之所以高效就是因为在固定其他参数后,对一个参数优化过程很高效。
二. 符号定义与基础回顾
(1)先定义下述三个符号,以便后文表述:

(2)若为线性核函数分类,由基本二分类SVM可知,最后的分类是根据 w ∗ T x i + b ∗ w^{*T}x_i+b^* w∗Txi+b∗来判断的:若 w ∗ T x i + b ∗ > 0 w^{*T}x_i+b^*>0 w∗Txi+b∗>0则判断 y i y_i yi属于某一类,若 w ∗ T x i + b ∗ < 0 w^{*T}x_i+b^*<0 w∗Txi+b∗<0则判断 y i y_i yi属于另一类。如果是非线性核函数分类,则是 w ∗ T ϕ ( x i ) + b ∗ w^{*T}\phi(x_i)+b^* w∗Tϕ(xi)+b∗与0的大小比较(但是,在实际核函数模型中,我们没有 ϕ ( x i ) \phi(\bm x_i) ϕ(xi)的表达式,往往都是直接给出 Θ ( x i , x j ) \bm{\Theta(x_i,x_j)} Θ(xi,xj)(而: Θ ( x i , x j ) \bm{\Theta(x_i,x_j)} Θ(xi,xj)= ϕ ( x i ) T ϕ ( x j ) \phi(\bm x_i)^T\phi(\bm x_j) ϕ(xi)Tϕ(xj))。因此, w ∗ T x i + b ∗ w^{*T}x_i+b^* w∗Txi+b∗仅用于线性核函数中,而在非线性核函数里,并不用 w ∗ w^{*} w∗来判断分类的结果。虽然不用,但为了完整性,这里还是给出核函数下的 w ∗ w^{*} w∗), w ∗ \bm w^* w∗的具体表达式为:
w ∗ = ∑ i α i ∗ y i ϕ ( x i ) \begin{aligned} \bm{w^*}=\sum_{i}^{}\alpha_i^*y_i\phi(\bm x_i) \end{aligned} w∗=i∑αi∗yiϕ(xi)
而对标量 b ∗ b^* b∗的计算,书上式子(2.75)写道:

(3)符号 E i E_i Ei定义如下:
E i = f ( x i ) − y i = ( ∑ j = 1 n y j α j K i j + b ) − y i = ( ∑ j = 1 n y j α j ϕ ( x j ) T ϕ ( x i ) + b ) − y i = ( w ∗ T ϕ ( x i ) + b ) − y i \begin{aligned} E_i &=f(\bm x_i)-y_i\\&=(\sum_{j=1}^{n}y_j\alpha_jK_{ij}+b)-y_i \\&=(\sum_{j=1}^{n}y_j\alpha_j\phi(x_j)^T\phi(x_i)+b)-y_i \\&=(w^{*T}\phi(x_i)+b)-y_i \end{aligned} Ei=f(xi)−yi=(j=1∑nyjαjKij+b)−yi=(j=1∑nyjαjϕ(xj)Tϕ(xi)+b)−yi=(w∗Tϕ(xi)+b)−yi
显然, E i E_i Ei是函数 f ( x ) f(x) f(x)对输入 x i x_i xi的预测值与真实输出值 y i y_i yi之差。(备注:1998年原始参考文献中,预测值 f ( x i ) f(x_i) f(xi)用 u i u_i ui表示的,即 E i = u i − y i E_i=u_i-y_i Ei=ui−yi)
三. 整理目标函数

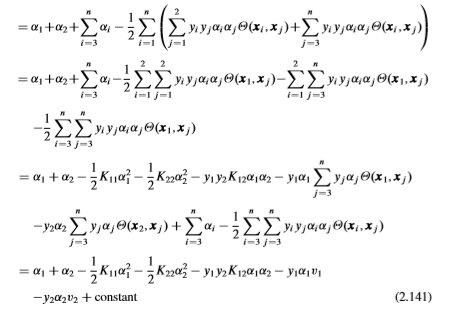
四. α 2 n e w \alpha_2^{new} α2new的推导(不考虑范围约束时)
由于下述约束条件成立:

因此,有

其中, C ′ C' C′是常数。根据式子(2.142),可知:
α 1 = γ − s α 2 \begin{aligned} \alpha_1 = \gamma -s\alpha_2 \end{aligned} α1=γ−sα2
其中 γ = C ′ y 1 \gamma=C'y_1 γ=C′y1、 s = y 1 y 2 s=y_1y_2 s=y1y2 (因为 y 1 y_1 y1只能取+1或-1,因此,除以 y 1 y_1 y1等价于乘以 y 1 y_1 y1)。带入消除 α 1 \alpha_1 α1后,我们可将式子(2.141)重新整理为下式:

将上式对 α 2 \alpha_2 α2求导,并令其为0,得到下式:
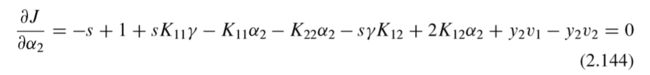
解出上式中的 α 2 \alpha_2 α2为:

上式(2.145)中, α 2 \alpha_2 α2有个上角标,是表示此为更新后的 α 2 \alpha_2 α2,或者说是最优的 α 2 \alpha_2 α2,用 α 2 n e w \alpha_2^{new} α2new表示。
上式经过下面照片中的推导可以化简,详细推导过程见照片(可省略不看):

推导结果为:(此结果也是1998年中论文的结果)
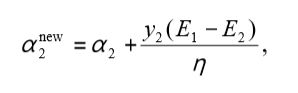
五. α 2 n e w , r e v i s e d \alpha_2^{new,revised} α2new,revised的推导
显然,上述分析没有考虑式子(2.97)的约束条件,换句话说, α 2 n e w \alpha_2^{new} α2new很可能不在指定区域 [ 0 , C ] [0,C] [0,C]内,而由于此时已经转化为一元函数求极值问题,所有,如果极点不在区域内,那么最值一定取在边界点,所有,最优的 α 2 \alpha_2 α2的取值不再是 α 2 n e w \alpha_2^{new} α2new,应该换符号表示,文中采用 α 2 n e w , r e v i s e d \alpha_2^{new,revised} α2new,revised表示考虑式子(2.97)中约束的新更新变量。故为了分析式子(2.97)的约束条件,有下述两个公式:
(1)当 y 1 y_1 y1与 y 2 y_2 y2异号时
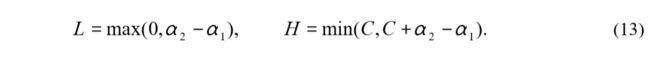
(2)当 y 1 y_1 y1与 y 2 y_2 y2同号时

解释一下上述公式:
首先将式子(2.142)两侧同时乘以 y 1 y_1 y1,由于 y 1 y_1 y1只能取正负1,故,分类讨论:
(1)解释:当 y 1 y_1 y1与 y 2 y_2 y2异号,所以有:
α 1 + α 2 = γ \begin{aligned} \alpha_1+\alpha_2=\gamma \end{aligned} α1+α2=γ
由于 α 1 \alpha_1 α1与 α 2 \alpha_2 α2只能取[0,C]之间的box内,所以,此时有两种情况,如图:

(2)解释:当 y 1 y_1 y1与 y 2 y_2 y2同号时,有:

综合上述两种情况,我们有:
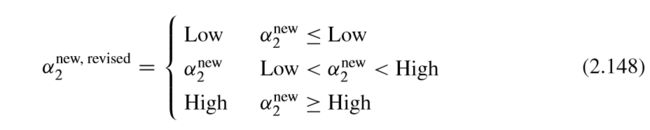
此时得到的 α 2 n e w , r e v i s e d \alpha_2^{new,revised} α2new,revised是完全符合题意的最优的 α 2 \alpha_2 α2值!下面回带如公式,反求最优的 α 1 \alpha_1 α1。
六. α 1 n e w \alpha_1^{new} α1new的推导
由于式子 (2.142)成立(且,算法流程中已提及,叠代 α 1 \alpha_1 α1与 α 2 \alpha_2 α2时,需要固定其余参数,即 α 3 \alpha_3 α3到 α n \alpha_n αn是固定不变的,只叠代 α 1 \alpha_1 α1与 α 2 \alpha_2 α2),因此,迭代前后的 α 1 \alpha_1 α1与 α 2 \alpha_2 α2都满足下式:
y 1 α 1 o l d + y 2 α 2 o l d = C ′ \begin{aligned} y_1\alpha_1^{old}+y_2\alpha_2^{old}=C' \end{aligned} y1α1old+y2α2old=C′
y 1 α 1 n e w + y 2 α 2 n e w = C ′ \begin{aligned} y_1\alpha_1^{new}+y_2\alpha_2^{new}=C' \end{aligned} y1α1new+y2α2new=C′
所以有:
y 1 α 1 o l d + y 2 α 2 o l d = y 1 α 1 n e w + y 2 α 2 n e w \begin{aligned} y_1\alpha_1^{old}+y_2\alpha_2^{old}=y_1\alpha_1^{new}+y_2\alpha_2^{new} \end{aligned} y1α1old+y2α2old=y1α1new+y2α2new
上述左右同时乘以 y1,可解出 α 1 n e w \alpha_1^{new} α1new如下:

七. KKT条件
下式KKT条件中的 f ( x i ) f(x_i) f(xi),代表在当前 w w w这个分类准则下,输入为 x i x_i xi时,输出的分类预测结果。

(此处的KKT推导见2001年论文即可!)这个KKT条件说明,在两条间隔线外面的点,对应前面的系数 α i \alpha_i αi为0(即距离线很远且不起作用的点),在两条间隔线里面的对应 α i \alpha_i αi为C,在两条间隔线上的对应的系数 α i \alpha_i αi在0和C之间。
八. b b b的推导
(1)先说结论:

解释为什么 α 1 n e w \alpha_1^{new} α1new和 α 2 n e w , c l i p p e d \alpha_2^{new,clipped} α2new,clipped在界内时( 0 < α i n e w < C 0<\alpha_i^{new}

(2)再说结论的证明过程:


之所以要更新 E i E_i Ei,是因为这个变量有两个作用,一是用以作为第二个乘子的选取因子;二是用以作为判断算法终止的条件!
九. SMO应用流程
下面是SMO算法详细流程,该流程比本文第一节中的要详细,可用于实际应用中:


其中,用启发式算法选取点的原则为:

十. 其余说明:
(1)论文中说,如果采用的是线性核函数,那么久按照如下方式更新 w n e w \bm w^{new} wnew:
w n e w = w + y 1 ( α 1 n e w − α 1 ) x 1 + y 2 ( α 2 n e w , r e v i s e d − α 2 ) x 2 \begin{aligned} \bm w^{new}=\bm w+y_1(\alpha_1^{new}-\alpha_1)\bm x_1+y_2(\alpha_2^{new,revised}-\alpha_2)\bm x_2 \end{aligned} wnew=w+y1(α1new−α1)x1+y2(α2new,revised−α2)x2
上式的结论依据以下两个公式便可得到:

看完这句话以后我误会了好久,仔细看公式才发现,之所以文中说“线性核函数”才更新 w n e w \bm w^{new} wnew,是因为这里的更新公式中没有 ϕ ( . ) \phi(.) ϕ(.),换言之,并不是 w \bm w w只能用于线性,而是这里的公式没有加核,所以,这个公式里的 w \bm w w只能用于线性。若改为下式,则任何满足题意的核,都可以用此式来分类:
w n e w = w + y 1 ( α 1 n e w − α 1 ) ϕ ( x 1 ) + y 2 ( α 2 n e w , r e v i s e d − α 2 ) ϕ ( x 2 ) \begin{aligned} \bm w^{new}=\bm w+y_1(\alpha_1^{new}-\alpha_1)\bm \phi(x_1)+y_2(\alpha_2^{new,revised}-\alpha_2)\bm \phi(x_2) \end{aligned} wnew=w+y1(α1new−α1)ϕ(x1)+y2(α2new,revised−α2)ϕ(x2)
(按照更新 α 1 \alpha_1 α1与 α 2 \alpha_2 α2的方式,来更新所有需要更新的 α i \alpha_i αi,全部训练并更新完后,便可将该模型用于分类,最终的 w n e w \bm w^{new} wnew可按照上述更新两个参数的方式来推导,但是正如前文所述说,实际中直接给出的是 Θ ( x i , x j ) \bm{\Theta(x_i,x_j)} Θ(xi,xj)的矩阵取值( Θ ( x i , x j ) \bm{\Theta(x_i,x_j)} Θ(xi,xj)= ϕ ( x i ) T ϕ ( x j ) \phi(\bm x_i)^T\phi(\bm x_j) ϕ(xi)Tϕ(xj)),并非 ϕ ( x i ) \phi(\bm x_i) ϕ(xi)。因此,非线性核函数下的 w n e w \bm w^{new} wnew没有实际用处,仅用于求解 b n e w b^{new} bnew
(2)另外一个待更新资料:

下文中,迭代的终止条件是两次叠代的 α o l d \alpha_{old} αold与 α n e w \alpha_{new} αnew所对应的 f i o l d f_i^{old} fiold与 f i n e w f_i^{new} finew之间的数值小于某个数时,则终止叠代。毕竟选取的 α 1 \alpha_1 α1都是那些不满足KKT条件的,当都满足以后,自然每次叠代 α \alpha α后,其 f f f改进就会很小了。

算法中,各个所需的阿尔法求解完毕后(即样本训练结束以后),最终应用时分类的原则为:

十一. SMO改进(个人记录):
问题所在:(举例)

计算如下:(为了清晰地凸显出1998年SMO的缺点,下文的更新中,同时叠代了 “传统的 b b b” 和 “新颖的 b l o w 、 b u p b_{low}、b_{up} blow、bup”)
(1)第一次迭代更新计算:
此时所有 α \alpha α都为0,初始类别为 y 1 = − 1 ; y 2 = + 1 ; y 3 = + 1 y_1=-1; y_2=+1;y_3=+1 y1=−1;y2=+1;y3=+1,因此可计算得: F 1 = 1 ; F 2 = − 1 ; F 3 = − 1 F_1=1; F_2=-1;F_3=-1 F1=1;F2=−1;F3=−1,1,2,3三个样本点分别属于 I 4 、 I 1 、 I 1 I_4、I_1、I_1 I4、I1、I1,因此 b l o w = 1 、 b u p = − 1 b_{low}=1、b_{up}=-1 blow=1、bup=−1。由于 α \alpha α都为0,因此 f ( x i ) = ∑ j = 1 n y j α j K i j − b = − b = 0 f(x_i)=\sum_{j=1}^{n}{y_j\alpha_jK_{ij}-b=-b=0} f(xi)=∑j=1nyjαjKij−b=−b=0(i=1,2,3),因此由公式 E i = f ( x i ) − y i E_i=f(x_i)-y_i Ei=f(xi)−yi计算得: E 1 = 1 ; E 2 = − 1 ; E 3 = − 1 E_1=1; E_2=-1;E_3=-1 E1=1;E2=−1;E3=−1。此外,容易计算初始状态的三个节点都违背KKT条件。
(2)第二次迭代更新计算:
α 2 n e w = 0 + 1 ( 1 + 1 ) 1 + 1 − 0 = 1 \alpha_2^{new}=0+\frac{1(1+1)}{1+1-0}=1 α2new=0+1+1−01(1+1)=1
L = m a x ( 0 , α 2 − α 1 ) = 0 L=max(0,\alpha_2-\alpha_1)=0 L=max(0,α2−α1)=0
H = m i n ( C , C + α 2 − α 1 ) = C = 1 4 H=min(C,C+\alpha_2-\alpha_1)=C=\frac{1}{4} H=min(C,C+α2−α1)=C=41
α 2 n e w , c l i p p e d = H = C = 1 4 \alpha_2^{new,clipped}=H=C=\frac{1}{4} α2new,clipped=H=C=41
α 1 n e w = 0 + ( − 1 ) ( 0 − 1 4 ) = 1 4 \alpha_1^{new}=0+(-1)(0-\frac{1}{4})=\frac{1}{4} α1new=0+(−1)(0−41)=41
因此,可知, α 1 n e w = α 2 n e w = C \alpha_1^{new}=\alpha_2^{new}=C α1new=α2new=C,此时都是上界!(按照传统SMO中所提的算法,此时的b的更新公式为 b 1 b_1 b1与 b 2 b_2 b2的平均值)。下面继续更新叠代:
F 1 = ∑ j = 1 n α j y j K 1 j − y 1 = 1 4 ( − 1 ) ( 1 ) + 0 + 0 + 1 = 3 4 F_1=\sum_{j=1}^{n}{\alpha_jy_jK_{1j}-y_1=\frac{1}{4}(-1)(1)+0+0+1=\frac{3}{4}} F1=∑j=1nαjyjK1j−y1=41(−1)(1)+0+0+1=43
F 2 = 0 + 1 4 ( 1 ) ( 1 ) + 0 − 1 = − 3 4 F_2=0+\frac{1}{4}(1)(1)+0-1=-\frac{3}{4} F2=0+41(1)(1)+0−1=−43
F 3 = 0 + 1 4 ( 1 ) ( 2 ) + 0 − 1 = − 1 2 F_3=0+\frac{1}{4}(1)(2)+0-1=-\frac{1}{2} F3=0+41(1)(2)+0−1=−21
下面按照1998年论文的步骤更新参数 b b b

b 1 n e w = 1 + ( − 1 ) ( 1 4 − 0 ) ( 1 ) + ( 1 ) ( 1 4 − 0 ) = 3 4 b_1^{new}=1+(-1)(\frac{1}{4}-0)(1)+(1)(\frac{1}{4}-0)=\frac{3}{4} b1new=1+(−1)(41−0)(1)+(1)(41−0)=43
b 2 n e w = − 3 4 b_2^{new}=-\frac{3}{4} b2new=−43
注意,若仔细按照《统计学习方法》中的步骤推导b的公式,则发现,其实这里b的更新公式中,用到的 E i E_i Ei其实是 E i o l d E_i^{old} Eiold,正因为是old,所以b中的公式里才要减去old并加上new的那一项,因此,标准低来写,上图中,用以计算 b 1 b_1 b1和 b 2 b_2 b2的公式(20)和公式(21)的实质由下式化简而来: b 1 n e w = f n e w ( x i ) − y i b_1^{new}=f^{new}(x_i)-y_i b1new=fnew(xi)−yi,其中的 f n e w ( x i ) f^{new}(x_i) fnew(xi)中是更新后的新 α \alpha α计算的,带入后就分别等于公式(20)和公式(21)了。(其中, f n e w ( x 1 ) = ∑ j = 1 3 y j α j K i j − b o l d = ( − 1 ) ( 1 4 ) ( 1 ) + 0 + 0 − 0 = − 1 4 f^{new}(x_1)=\sum_{j=1}^{3}{y_j\alpha_jK_{ij}-b^{old}=(-1)(\frac{1}{4})(1)+0+0-0=-\frac{1}{4}} fnew(x1)=∑j=13yjαjKij−bold=(−1)(41)(1)+0+0−0=−41或者也可以直接用 f n e w ( x 1 ) = b 1 n e w + y 1 = − 1 4 f^{new}(x_1)=b_1^{new}+y_1=-\frac{1}{4} fnew(x1)=b1new+y1=−41,同理, f n e w ( x 2 ) = 1 4 f^{new}(x_2)=\frac{1}{4} fnew(x2)=41, f n e w ( x 3 ) = 1 2 f^{new}(x_3)=\frac{1}{2} fnew(x3)=21)。注意!!!上述 f n e w ( x i ) f^{new}(x_i) fnew(xi)的取值并没有在SMO代码中出现,换句话说,下一轮迭代时所采用的 f n e w ( x i ) f^{new}(x_i) fnew(xi)并不是上述计算的取值,上述的取值只是理论上的 f n e w ( x i ) f^{new}(x_i) fnew(xi);而在传统SMO中实际运行时的 f n e w ( x i ) f^{new}(x_i) fnew(xi)由于使用了不恰当的b(即: b = b 1 + b 2 2 b=\frac{b_1+b_2}{2} b=2b1+b2更新的),而出现弊端,这也正是2001年论文的精髓所在,具体在第三次迭代中详细说明。论文的截图中, b n e w b^{new} bnew的计算用的是 F 1 F_1 F1与 F 2 F_2 F2的均值,并非 b 1 b_1 b1与 b 2 b_2 b2的均值,这是因为,在更新 b 1 b_1 b1与 b 2 b_2 b2时,我们假设了此时的两个 α \alpha α都位于界内(即0与C的开区间上),而界内的含义是该样本点表示支撑向量!根据KKT条件中的第二个限制可知(看本博客上方的KKT,或参见《统计学习方法》中的公式7.112)此时的 y i f ( x i ) = 1 y_if(x_i)=1 yif(xi)=1,我们若将此式左右同乘以 y i y_i yi,则有: f ( x i ) = y i f(x_i)=y_i f(xi)=yi,即: f ( x i ) − y i = 0 f(x_i)-y_i=0 f(xi)−yi=0,而根据 E i E_i Ei定义, E i = f ( x i ) − y i E_i=f(x_i)-y_i Ei=f(xi)−yi,所以我们可知,对满足KKT条件且在界内的样本点而言,其误差 E i = 0 E_i=0 Ei=0,而论文中有如下定义:
E i = f ( x i ) − y i = F i − β i E_i=f(x_i)-y_i=F_i-\beta_i Ei=f(xi)−yi=Fi−βi
上述公式说明: E i = f ( x i ) − y i E_i=f(x_i)-y_i Ei=f(xi)−yi是1998年论文的定义。 E i = F i − β i E_i=F_i-\beta_i Ei=Fi−βi是2001年论文的定义,两者相等是显然的,因为 F i = ∑ j = 1 n α j y j K i j − y i F_i=\sum_{j=1}^{n}{\alpha_jy_jK_{ij}-y_i} Fi=∑j=1nαjyjKij−yi,而 f ( x i ) = ∑ j = 1 n α j y j K i j − b f(x_i)=\sum_{j=1}^{n}{\alpha_jy_jK_{ij}-b} f(xi)=∑j=1nαjyjKij−b,且 b = β b=\beta b=β。
因此,在该限制条件下(界内且满足KKT,由于19981年中loop1与loop2的叠代保证会使得参数满足KKT), F i = β i F_i=\beta_i Fi=βi,所以,2001年论文中,计算b才有截图所示的 β = F 1 + F 2 2 = ( − 3 4 ) + 3 4 2 = 0 \beta=\frac{F_1+F_2}{2}=\frac{(-\frac{3}{4})+\frac{3}{4}}{2}=0 β=2F1+F2=2(−43)+43=0。
此时继续更新,由于此时的 α 1 = C \alpha_1=C α1=C, α 2 = C \alpha_2=C α2=C, α 3 = 0 \alpha_3=0 α3=0,再结合仍然不变的 y 1 = − 1 ; y 2 = + 1 ; y 3 = + 1 y_1=-1; y_2=+1;y_3=+1 y1=−1;y2=+1;y3=+1,因此,此三个样本点分别属于 I 2 I_2 I2、 I 3 I_3 I3、 I 1 I_1 I1。并且此时的三个 F i F_i Fi已经计算好了。因此,根据 b u p b_{up} bup和 b l o w b_{low} blow的计算公式,可知:
b u p = m i n { 3 4 , − 1 2 } = − 1 2 b_{up}=min{\{\frac{3}{4},-\frac{1}{2}}\}=-\frac{1}{2} bup=min{43,−21}=−21
b l o w = m a x { − 3 4 } = − 3 4 b_{low}=max{\{-\frac{3}{4}}\}=-\frac{3}{4} blow=max{−43}=−43
(3)第三次迭代更新计算:
此时我们会惊奇地发现,用原始的b来计算时,我们发现原本计算好的 α \alpha α又不满足了KKT条件…究其原因是因为b的选取不合适,因此才需要用 b l o w 、 b u p b_{low}、b_{up} blow、bup代替。若按照传统SMO代码来更新 f n e w ( x i ) f^{new}(x_i) fnew(xi),则要用到上文计算的b,其中的b=0(由公式 β = F 1 + F 2 2 = ( − 3 4 ) + 3 4 2 = 0 \beta=\frac{F_1+F_2}{2}=\frac{(-\frac{3}{4})+\frac{3}{4}}{2}=0 β=2F1+F2=2(−43)+43=0计算而来!并没有采用上文中的 b i n e w b_i^{new} binew,这里与上文加粗字体处相呼应!),因此,传统SMO计算 f n e w ( x i ) f^{new}(x_i) fnew(xi)公式如下:
f n e w ( x 1 ) = ∑ j = 1 3 y j α j K 1 j − β = − 1 4 f^{new}(x_1)=\sum_{j=1}^{3}{y_j\alpha_jK_{1j}-\beta}=-\frac{1}{4} fnew(x1)=∑j=13yjαjK1j−β=−41

论文中说此时,用 β = 0 \beta=0 β=0计算时,违背了KKT,但是我验证好像没有违背啊???但是后来该大佬重复发表的此篇论文中,没有这个例子了。
即使这个例子不合理,但是这个事实是成立的!因此,在1998年的SMO中,才有不断地循环loop2的事情,一直到loop2中所有参数都满足KKT后,才能重新循环loop1,并更新新的参数!而不断循环loop2的原因就在此,即b的选取是病态的,尤其是当 α \alpha α的取值在边界上( α = C \alpha=C α=C时),此时最容易出现b取值不合理,正因为b的不合理,因此导致loop2不断地迭代循环,一直到所有参数都满足KKT才结束,才能让examineAll=1并执行loop1。
2001年论文中的其余注意事项:
第二次读2001年论文的感悟:
注意,不是原来的β不正确,而是KKT的判断中有β的参与而导致低效!因此,本文更改KKT的判断,令其脱离β!因此,将β从KKT公式中分离出来,然后比较β两侧的大小关系即可!由此实现高效的SMO叠代!!!
(发现第一次读的理解有偏差…)
参考资料:
[1] 《Sequential Minimal Optimization:
A Fast Algorithm for Training Support Vector Machines》 作者:John C. Platt 时间:1998 (SMO原文)
[2] 《Selected Applications of Convex Optimization》作者:Li Li
[3] 学习网址1
[4] 学习网址2
[5] SMO算法的matiab代码下载网址1
[6] SMO算法的matiab代码下载网址2
[7] SMO算法的matiab代码下载网址3
[7] 从SVM到SMO详细讲解
[8] 简化的SMO伪代码
[9] C_SVC 和 V_SVC区别