计算机视觉——HARRIS角点检测
HARRIS角点检测
- 1. 基本思想
- 2. 基本原理
- 2.1 HARRIS数学表达式
- 2.2 角点响应函数
- 2.3 角点计算流程
- 3. 实验过程
- 3.1 数据准备
- 3.2 代码实现
- 4. 实验结果分析
- 4.1 数据一实验结果对比
- 4.2 数据二的实验结果对比
- 4.3 数据三的实验结果对比
- 5. 实验结果分析总结
- 6. 实验遇到的问题
1. 基本思想
Harris角点检测算子是于1988年由CHris Harris & Mike Stephens提出来的。
好的角点检测算法有以下特点:
• 检测出图像中“真实的”角点
• 准确的定位性能
• 很高的稳定性
• 具有对噪声的鲁棒性
• 具有较高的计算效率
HARRIS角点检测基本思想:从图像局部的小窗口观察图像特征。
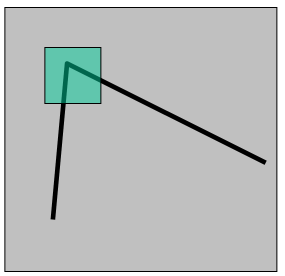
在进行原理分析之前需明确以下概念:
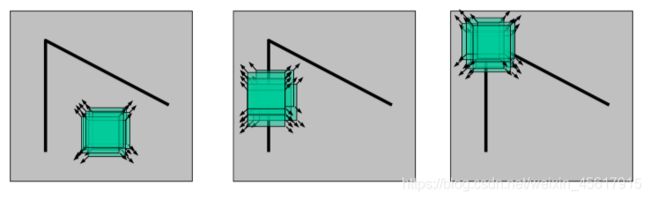
平坦区域: 任意方向移动,无灰度变化
边缘:沿着边缘方向移动,无灰度变化
角点:窗口向任意方向的移动都导致图像灰度的明显变化。
2. 基本原理
2.1 HARRIS数学表达式
将窗口平移 [ u , v ] [u,v] [u,v]产生灰度变化 E ( u , v ) E(u,v) E(u,v)的表达式如下:
E ( u , v ) = ∑ x , y w ( x , y ) [ I ( x + u , y + v ) − I ( x , y ) ] 2 E(u,v)=\displaystyle\sum_{x,y}w(x,y)[I(x+u,y+v)-I(x,y)]^2 E(u,v)=x,y∑w(x,y)[I(x+u,y+v)−I(x,y)]2 (1)
其中:
w ( x , y ) w(x,y) w(x,y)为窗口函数
I ( x + u , y + v ) I(x+u,y+v) I(x+u,y+v)为平移后的图像灰度
I ( x , y ) ) I(x,y)) I(x,y))为图像灰度
通过利用二元泰勒近似可将表达式(1)化简,化简过程如下:
将 I ( x + u , y + v ) I(x+u,y+v) I(x+u,y+v)函数在 ( x , y ) (x,y) (x,y)处泰勒展开,得:
I ( x + u , y + v ) = I ( x , y ) + I x u + I y v + O ( u 2 , v 2 ) I(x+u,y+v)=I(x,y)+I_xu+I_yv+O(u^2,v^2) I(x+u,y+v)=I(x,y)+Ixu+Iyv+O(u2,v2)
则有:
E ( u , v ) = ∑ x , y w ( x , y ) [ I x u + I y v + O ( u 2 , v 2 ) ] 2 ≈ ∑ x , y w ( x , y ) [ I x u + I y v ] 2 E(u,v)=\displaystyle\sum_{x,y}w(x,y)[I_xu+I_yv+O(u^2,v^2)]^2 ≈\displaystyle\sum_{x,y}w(x,y)[I_xu+I_yv]^2 E(u,v)=x,y∑w(x,y)[Ixu+Iyv+O(u2,v2)]2≈x,y∑w(x,y)[Ixu+Iyv]2 (2)
其中,
[ I x u + I y v ] 2 = [ u , v ] [ I x 2 I x I y I x I y I y 2 ] [ u v ] [I_xu+I_yv]^2 = [u,v]\begin{bmatrix} I_x^2&I_xI_y\\ I_xI_y&I_y^2\end{bmatrix}\begin{bmatrix} u\\ v\end{bmatrix} [Ixu+Iyv]2=[u,v][Ix2IxIyIxIyIy2][uv]
也是对于局部微小的移动量 [ u , v ] [u,v] [u,v],可以近似得到下面的表达:
E ( u , v ) ≅ [ u , v ] M [ u v ] E(u,v)\cong\begin{bmatrix}u,v\end{bmatrix} M \begin{bmatrix}u\\v\end{bmatrix} E(u,v)≅[u,v]M[uv]
其中M是2*2矩阵,可由图像的导数求得:
M = ∑ x , y w ( x , y ) [ I x 2 I x I y I x I y I y 2 ] M = \displaystyle\sum_{x,y}w(x,y)\begin{bmatrix} I_x^2&I_xI_y\\ I_xI_y&I_y^2\end{bmatrix} M=x,y∑w(x,y)[Ix2IxIyIxIyIy2]
窗口移动导致的图像变化量:实对称矩阵M的特征值分析
E ( u , v ) ≅ [ u , v ] M [ u v ] E(u,v)\cong\begin{bmatrix}u,v\end{bmatrix} M \begin{bmatrix}u\\v\end{bmatrix} E(u,v)≅[u,v]M[uv]
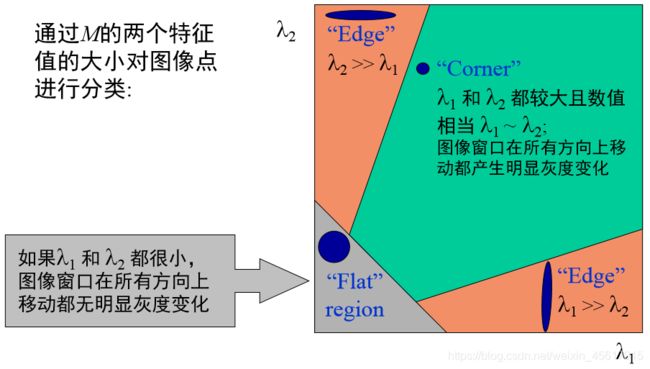
记M的特征值为 λ 1 , λ 2 \lambda_1,\lambda_2 λ1,λ2.
2.2 角点响应函数
定义:角点响应函数R
R = d e t M − k ( t r a c e M ) 2 R=detM-k(traceM)^2 R=detM−k(traceM)2
d e t M = λ 1 λ 2 detM=\lambda _1\lambda _2 detM=λ1λ2
t r a c e M = λ 1 + λ 2 traceM=\lambda _1+\lambda _2 traceM=λ1+λ2
( k − e m p i r i c a l c o n s t a n t , k = 0.04 0.06 ) (k-empirical constant,k=0.04~0.06) (k−empiricalconstant,k=0.04 0.06)
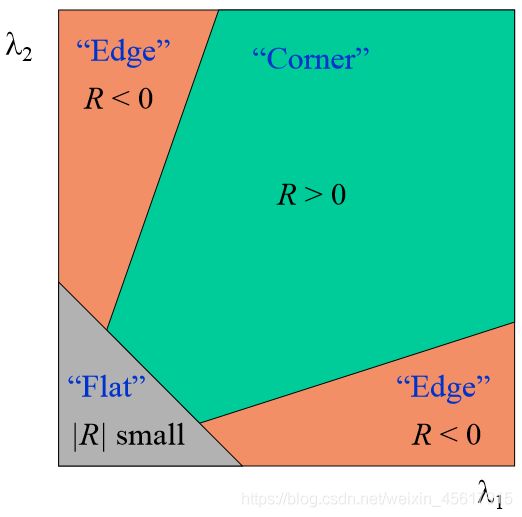
R 只与M的特征值有关
角点:R 为大数值正数
边缘:R为大数值负数
平坦区:R为小数值
2.3 角点计算流程
- 对焦点响应函数R进行阈值处理
R > t h r e s h o l d R>threshold R>threshold - 提取R的局部最大值
为了消除参数k的影响,也可采用商来计算响应:
R = d e t M t r a c e M 2 R=\frac{detM}{traceM^2} R=traceM2detM
d e t M = λ 1 λ 2 detM=\lambda _1\lambda _2 detM=λ1λ2
t r a c e M = λ 1 + λ 2 traceM=\lambda _1+\lambda _2 traceM=λ1+λ2
3. 实验过程
3.1 数据准备
实验进行之前进行拍摄物体图片,以下是准备进行实验的图片:
数据一:纹理平坦的图像

数据二:角点丰富的图像

数据三:边缘丰富的图像

3.2 代码实现
Harris角点检测的python代码实现主要是通过调用PCV包中自带的harris.py文件中的函数。
compute_harris_response(im,sigma=3)
对于灰度图像中的每个像素,计算Harris角探测器响应函数。
get_harris_points(harrisim,min_dist=10,threshold=0.1)
返回harris角点检测到的点。
get_descriptors(image,filtered_coords,wid=5)
画出harris角点检测到的点。
# -*- coding: utf-8 -*-
from pylab import *
from PIL import Image
from PCV.localdescriptors import harris
# 读入图像
im = array(Image.open('1.jpg').convert('L'))
# 检测harris角点
harrisim = harris.compute_harris_response(im)
# Harris响应函数
harrisim1 = 255 - harrisim
figure()
gray()
#画出Harris响应图
subplot(221)
imshow(harrisim1)
print (harrisim1.shape)
axis('off')
axis('equal')
threshold = [0.01, 0.05, 0.1]
for i, thres in enumerate(threshold):
filtered_coords = harris.get_harris_points(harrisim, 6, thres)
subplot(2, 2, i+2)
imshow(im)
print (im.shape)
plot([p[1] for p in filtered_coords], [p[0] for p in filtered_coords], '*')
axis('off')
show()
4. 实验结果分析
4.1 数据一实验结果对比
正面图像运行结果:

侧面图像运行结果:

旋转180°图像运行结果:

尺度变大图像运行结果:

光照变暗图像运行结果:

4.2 数据二的实验结果对比
正面图像运行结果:

侧面图像运行结果:

旋转180°图像运行结果:

尺度变大图像运行结果:

光照变暗图像运行结果:

4.3 数据三的实验结果对比
正面图像运行结果:

侧面图像运行结果:

旋转180°图像运行结果:

尺度变大图像运行结果:

光照变暗图像运行结果:

5. 实验结果分析总结
对于数据一、二、三不同条件下图像的运行结果分析可得:
- 对比正面图像和侧面图像的运行结果可以看出,对于图像中的标注稍有差异,由于侧面图像涵盖了正面图像所不能体现的细节特征,以及正面被遮挡的部分区域在侧面图像的角点检测中被检测到,所以显然有差距。
- 对比正面图图像和旋转180°的图像运行结果可以看出,角点的检测并无较大的差异。初步判断,图像只是进行旋转,而图像中的物体并没有发生质的变化,所以在角点检测时并没有大的差别。回到harris的原理中分析可得:Harris角点检测算子使用的是角点附近的区域灰度二阶矩矩阵。而二阶矩矩阵可以表示成一个椭圆,椭圆的长短轴正是二阶矩矩阵特征值平方根的倒数。当特征椭圆转动时,特征值并不发生变化,所以判断角点响应值R也不发生变化。
- 对比正面图像和尺寸变大的图像,可以发现检测结果有较大变化,当图像被缩小时,在检测窗口尺寸不变的前提下,在窗口内所包含图像的内容是完全不同的。左侧的图像可能被检测为边缘或曲线,而右侧的图像则可能被检测为一个角点。
- 对比正面图像和光照变暗图像可以发现,Harris角点检测算子对光照的变化不敏感,在进行Harris角点检测时,使用了微分算子对图像进行微分运算,而微分运算对图像密度的拉升或收缩和对亮度的抬高或下降不敏感。换言之,对亮度和对比度的仿射变换并不改变Harris响应的极值点出现的位置。
对于阈值不同的运行结果分析可得:
根据每一个运行结果的四张图像进行对比,可以发现,检测点逐渐变少。可得:增大阈值,将减小角点响应R,降低角点检测的灵性,减少被检测角点的数量;减小阈值,将增大角点响应值R,增加角点检测的灵敏性,增加被检测角点的数量。
对比三种场景下的数据一、二、三可以发现:
较大场景的检测结果比较丰富,而较为单一的图像检测点较少。初步判断为:较大场景涵盖的物体较多且各个像素点间的灰度值相差较大,检测到的角点数目较多。
6. 实验遇到的问题

经过查找原因可得,在展示运行结果的时候,在代码中添加了中文字体,但在使用中文前并未导入中文字体样式,而发生报错。
解决方法如下:
在代码的前面加入如下代码即可解决问题:
# 添加中文字体支持
from matplotlib.font_manager import FontProperties
font = FontProperties(fname=r"c:\windows\fonts\SimSun.ttc", size=14)