最小异或生成树
知识前缀:
字典树
原先学长讲过(忘了…)

画的不太好。意思就是那个意思(冒汗…)
字典树:听名字就是一颗树,Trie又被称为前缀树、字典树,所以当然是一棵树。上面这棵Trie树包含的字符串集合是{in, inn, int, tea, ten, to}。每个节点的编号是我们为了描述方便加上去的。树中的每一条边上都标识有一个字符。这些字符可以是任意一个字符集中的字符。比如对于都是小写字母的字符串,字符集就是’a’-‘z’;对于都是数字的字符串,字符集就是’0’-‘9’;对于二进制字符串,字符集就是0和1。
原理
从根节点开始,根节点是没有字符的。整体来说就是有一些字符串构成的一颗树,每个结点代表一个字符,我们从上往下读就会找到对应的单词,就像上面的 ab 从根节点往下读,仙都到a然后往下读b 读到b 我们明显发现b 是黄圈,这就是我们的一个标记。标记到这个点是一个单词。当然插入的时候会出现分支就像:aba和abbb这两个当我们插入完aba
我们从上往下插入a已经有了往下插入,下个字符b 也已经有了,再往下,下个字符b没有,就开设新节点。然后再往下。下个字符b也没有,在开设新节点。
这是插入:
/**这里说的是 a-z 如果不是这样连续的也可以强制规范或者类似hash函数的那种**/
const int maxn = 1000000 + 10; //字典树的最大结点数
const int m = 26; //字符集的个数
int trie[maxn][m] = {0};
int color[maxn] = {0}; //是否是一个字符串的终结点
int k = 1; //当前树中存在的结点个数
void insert(char *w){ //将字符串w插入到字典树中
int len = strlen(w); //每个字符都要插入,所以先取长度
int p = 0; //从根结点开始找
for(int i=0; i<len; i++){ //每个字符进行判断
int c = w[i] - 'a'; //c表示当前字符在字符集的第几个位置
if(!trie[p][c]){ //p结点没有字符w[i]的边
trie[p][c] = k; //增加一条边,k是另一端结点编号
k++; //结点数+1
}
p = trie[p][c]; //如果有边,更新p,从下一个结点查找
}
color[p] = 1; //循环结束,p结点为终结点
}
查询:
就是给出你一个字符串然后从原本给出的那些字符串中看是否能找到他。
这时候我们小黄圈标记的点就排上用场了。
小黄圈标记的代表从头到这个地方有对应的字符串。
解释一下程序吧:从头开始找第一个字符树中是否存在,不存在直接就是原先字符串堆中不可能存在你要找的字符串,若存在的话往下一个结点查询,…到最后你就判断最后一个结点有无颜色(就是确定有无该字符串而非前缀字符串)就像上图 如果要找到abb 的话。他是abbb的前缀子串但他并不是原字符串堆中的字符串,所以这就体现除了小黄圈的价值了。
int search(char *s){ //返回0,找不到,返回1,找到了
int len = strlen(s);
int p = 0;
for(int i=0; i<len; i++){
int c = s[i] - 'a';
if(!trie[p][c]) return 0; //没有边,字符串不存在
p = trie[p][c]; //有边,接着找
}
return color[p] == 1; //是否是终结点,例如,Trie树包含的字符串是"inn",你要查找的是"in",显然不存在字符串"in"
}
还有一种就是查找是否有前缀字符串的那种(也就是让你找的字符串的前缀是否在原字符串堆里)
int search(char *s){ //返回0,找不到,返回1,找到了
int len = strlen(s);
int p = 0;
for(int i=0; i<len; i++){
int c = s[i] - 'a';
//就是这一点的差距
if(color[p]) return 1;///如果有前缀字符串存在的话直接返回1
if(!trie[p][c]) return 0; //没有边,字符串不存在
p = trie[p][c]; //有边,接着找
}
return color[p] == 1; //是否是终结点,例如,Trie树包含的字符串是"inn",你要查找的是"in",显然不存在字符串"in"
删除
可能不大经常用这个

如果要删除这个图中的abbb 那么我们可以需要先找到abbb的最后一个结点一直往上删(找不到就说明不存在直接返回就行)如果是单个结点直接删去,而像这个黄圈b结点就不能删去
因为如果删去这个b 不仅会删去abbb 还会删去 ab和aba
所以我们删的原则是不影响其他字符串
int l;
inline void del(char *s){
int len=strlen(s),p=0;
for(int i=0;i<len;i++){
int c=s[i]-'a';
if(!trie[p][c]) return;//都没有这个字符串,就不用管它直接返回
int cnt= 0;
for(int j=0;j<26;j++) cnt += (bool)trie[p][i]; //有多少个结点
p=trie[p][i];
if(cnt>2) l=i+1;
if(color[p]) l=i+1;
}
if(!color[p]) return;//都没有这个字符串,就不用管它直接返回
color[p]=0;//删除字符串的末尾
for(int i=0;i<26;i++) if(trie[p][i]) return;//如果这个点有其他字符串要用就不能删除这个点
for(int i=l;i<len;i++) trie[p][s[i]-'a'] =0;//删除最近的没有分支的也就是只有一条链走到p的删除这些多余的边
}
完整代码:
#include白嫖吴老师的:(博主在偷乐)
#include 进入正题:
最小异或生成树
来吧先看代码,中的注解吧。一步步的分析。(我好菜)
先停一下:请开始我光神的表演
大写的 服
代码后面跟的就是解释呦,也不算是解释,就是我的的理解吧。举动自己的小矮人
这个啥都没有哈哈哈哈。。不扯淡了进入正题。
#include
#include
ans+=(1ll<<i);//第i为产生代价 就加上该代价,之所以 是从pos 开始到0 是因为这样的话都可以选择最优 因为 i越大产生的代价就越大 所以尽量的让其前面的一致这样就会缩小代价
}
}
return ans;
}
ll div(int gen,int pos){//gen 和pos 跟上面解释一样
if(trie[gen][0]&&trie[gen][1]){//如果既有左又有右 这一步就是左+右+合并
int x=trie[gen][0],y=trie[gen][1];///x代表 左端点的结点号,y代表右端点的节点号,x
ll minn=inf;
for(int i=l[x];i<=r[x];i++){//遍历一下用到左半树结点从小到大的数(输入的数)
minn=min(minn,answer(y,pos-1,a[i])+(1<<pos)); //解释一下 answer(y,pos-1,a[i])+(1<
}
return minn+div(trie[gen][0],pos-1)+div(trie[gen][1],pos-1); //合并+ 左+右
}
else if(trie[gen][0]) return div(trie[gen][0],pos-1);//如果只有左就直接是 左
else if(trie[gen][1]) return div(trie[gen][1],pos-1);//如果只有右就直接是 右
return 0;//如果都没有 肯定是0
}
}trie;
#define read read()
int main(){
trie.inint();//初始化
sf("%lld",&n);
for(int i=1;i<=n;i++) sf("%lld",&a[i]);
sort(a+1,a+1+n);
for(int i=1;i<=n;i++) trie.insert(a[i],i);
///tire.Traceback(0);
printf("%lld\n",trie.div(0,32));
return 0;
}
OK这就是理解吧。
首先我们以CF888G为例来说最小异或生成树。
首先我们生成一下样例一

它真正的异或状态其实是这样的,代价和就是每个边的权值(连接两点的异或值)
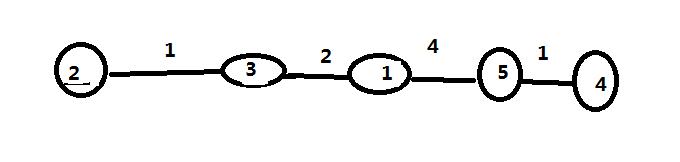
先这样看 给出你一个数 例如是x时那么与x相连的y要是x^y最小那么,x和y的二进制除了最后一位不一样剩下的都一样这样才最小,最小为1.如果x没有对应的除了二进制最后一位不一样其他都一样的,就往前面推一位,不断地扩大代价尝试。这样保证代价最小。之后是让最后两位不一样…………以此类推因为这样才能保证最后的异或和最小。那一下光神的图,(懒得画了)
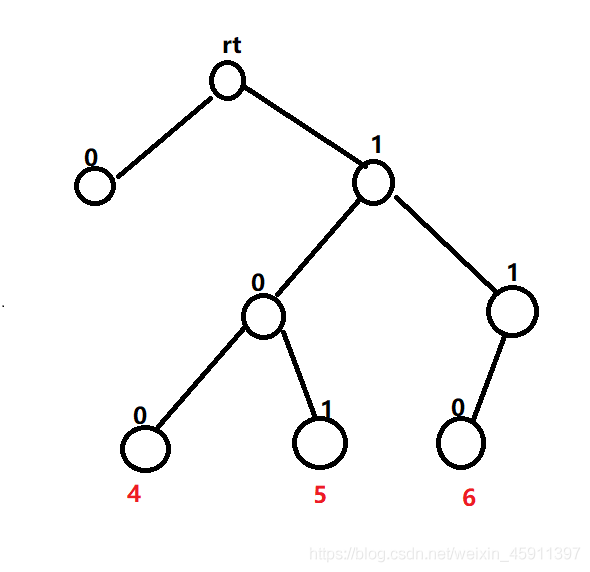
之所以4一定跟5匹配就是我上面说的,从最后一位往前推看是否除了该位其他二进制位都一样,显然4有5作伴,而6最后一位没有匹配的,所以往前推一位那就是4跟他异或最小。
这样其实还有一点没有体现到。(还要画个图,哭唧唧)

这个图更能让我理解这个吧。给出你2 ,3,5, 6四个数求这四个数的最小异或生成树,首先看2,根据上面说的他就是跟3匹配。
然后看5,没有4,那么我们继续往上推没有7,接下来我们应该推最后一位 因为这样的代价只是2+1,而你要是再往前推得话他就是4所以我们要从小代价开始。所以就是6,因为生成树他是通路,所以2-3 和5-6 还差一条边也就是左树和右树合并最小。所以就得出这个分治思想:一个节点下的最小异或生成树 = 左子树自己连接 + 右子树连接 + 左右合并时产生的最小值重点就是左右合并是产生的最小值,我们可以这样来找,固定一个不动,然后用另一个节点往其子节点搜看是否有对应匹配的?
其实就是这段代码(完整的去上面找啦):
for(int i=l[x];i<=r[x];i++){//遍历一下用到左半树结点从小到大的数(输入的数)
minn=min(minn,answer(y,pos-1,a[i])+(1<<pos)); //解释一下 answer(y,pos-1,a[i])+(1<
}
当只有左节点或者右节点,就是返回他自己。
总的来说构建这个最小异或生成树
就是把他按二进制来构建01字典树然后就是找两点异或最小在这两点上加边,边权值就是异或值最后形成一个生成树,然后把所有边权值相加,就是最后的结果。
牛客多校第五场B
上面是连接
题意:给你一棵树,你可以删除一些边或者增加一些边,但是在过程中必须保证图联通并且出现的任何一个环的异或和为0
这个其实就是用的最小异或生成树,也就是上面那个CF888G的代码,过需要改进一下,那个是给出个点,这个是给出边权值,所以需要转化一步。
struct node1{
ll e,next,w;
}edge[maxn];
ll head[maxn],cnt1=2;
void addedge(ll u,ll v,ll w){
edge[cnt1] = node1{v,head[u],w};
head[u] = cnt1++;
}
void dfs(ll u,ll fa,ll w){
a[u] = w;
for(int i=head[u];i;i=edge[i].next){
int e = edge[i].e;
if(e == fa) continue;
dfs(e,u,w^edge[i].w);
}
}
简单的说一下这个地方就是每个点到根节点的异或值(和最小生成树有些类似)其余步骤就跟CF那个一样来分析就行了。这个题算是CF的一个扩展就是将他给出的边权值转换成这样的点权值。