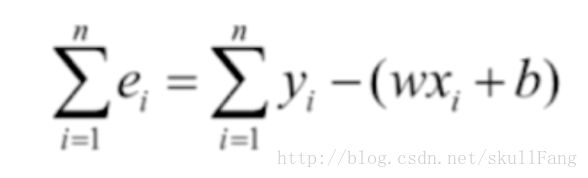神经网络——梯度下降&反向传播

前言

本篇是根据上一篇博文《神经网络–前向传播》续写的。
http://blog.csdn.net/skullFang/article/details/78620456
本文中的数学知识有点，需要一点微分的知识。（会求导）就可以。

基本概念

在上文我们已经知道了什么是前向传播。就是当前层的输入是上一层的输出，当前层的输出是下一层的输入。然后一层一层的传递下去。

反向传播也叫反向更新。根据感知机的原理。神经元产生输出之后要与正确的标签做一个对比然后更新调整自己的参数，经过反复训练达到一个很好的效果。

我们最后一层叫做输出层，这一层产生的输出就要与正确的输出做比较，然后更新自己的参数。那么神经网络有那么多层怎么去更新呢？答案就是反向更新。就是先最后一层的参数然后更新倒数第二层的参数、倒数第三层一直到第一层。这个就叫反向传播。

下面会一步一步解释为什么要这么做。

误差

根据前向传播原理
每一层的输出y是这样的到的。
z=wx+b
y=f(z)
其中 f(z)是激励函数。
我们可以观察到参数有 权重w，和偏置b。这个也是我们需要反向更新的参数。

因为反向传播主要是讨论参数问题，我们可以发现激励函数没有任何其他新的参数。(z还是w，b)组成。

我们暂且忽略激励函数的存在。
我们会得到公式:

y预测=wx+b

这里引入新的一个参数e（误差），这个e就是残差。
很容易得到公式
y真实=y预测+e
那么e=y真实-y预测
e=y真实-（wx+b）

对于每个表达式都是这样。所以我们加和之后变成了。

损失函数

因为e可能有正也有负，这样加和会导致相互抵消，所以我们要统一e的符号。统一e的符号只有两种方法。
1、取绝对值
2、取平方
我们使用第二种思路就是取平方。那么我们可以定义出一个损失函数。取名叫loss或者cost都可以。

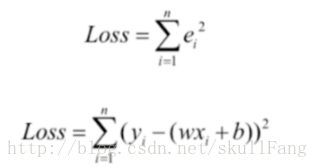
很容易就能得到loss的公式。

等等。。得到这个有啥用呢？有的人可能已经被公式绕晕了，看到这里不妨回去看看，我们为什么要做出这个loss函数。对！我们要找到它的最小值。

梯度下降

要取loss 的最小值，我首先想到的就是高数的求偏导之后，算极值点，这貌似对一元函数，二元函数比较靠谱，但是神经网络有那么多维度。显然不现实。（求偏导要玩疯）。
那么就整出了一个梯度下降算法。
我们首先看看loss函数

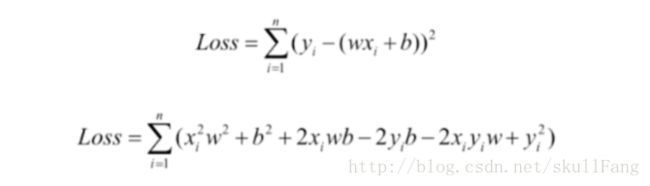
注意，我们这里是要更新w和b。那么我们这个函数的自变量是w和b哦。不是x,y。x,y看作常数。
那么我们提取一下公因式就会得到。

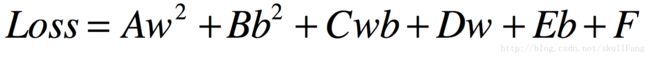
其中A、B、C、D、E、F是常数。
找到一个类似的函数

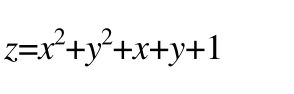
注意其中x对应的是w,y对应的是b。
画出图像

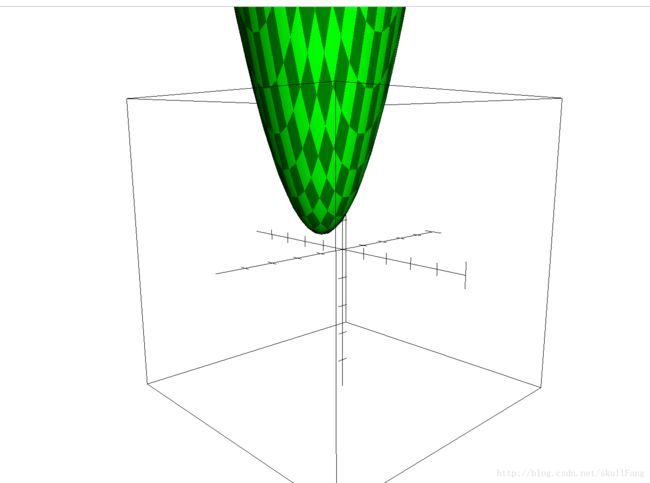
有点丑，将就看。

我们很容易看出，这个是像个碗（有点尖）既然是个碗的话，那么肯定有碗底，那么碗底就是我们要找到那个极小点。（不难理解吧）。
这就是一个二元凸函数。
怎么去找碗底现在就是我们要解决的问题。我们可以先去一维凸函数上看看。

一元凸函数

想要搞定找碗底的问题，先看看一维凸函数是怎么回事。

图像

求极值

由图像可以看出，凸吧！！！（凸个鬼，不应该是凹的么）。whatever。只是看这个图像的角度不一样吧。
怎么求极值呢？
这个简单，就是求导取导数等于0的点咯。。（说好不用这种方法）

那么我们的方法：
1、随便取一个点。
2、比较一下左右两边。
3、往小的那个方向滚动。
这个方法叫“挪动比较法”（自己编得名字）。
这个方法看似很靠谱，其实不靠谱。如果维度很高的话，每个维度需要比较两次（不同的方向），这对计算机来说计算量也有点大。

所以就造出来一个公式。

也就是说x的挪动方向直接跟自己的导数有关系。观察那个一元凸函数，我们稍微琢磨一下就可以知道。如果在x轴的正半轴上，那么导数肯定是是一个正书，我们减去这个正数。那么下一个x应该在往左边挪动。同样的如果在x轴的负半轴上，根据这个公式会往右边挪。慢慢挪就到了极值点了。神奇吧。这个的n是学习率（这个参数是手动调的）。就是每次挪动的步伐有多大。
这个东西在讲感知机的时候说过了。知道了一元凸函数求极值。我们再看看二元凸函数。

二元凸函数

图像

求极值

还是随便取一点，我们可以想象这个点在斜坡上面。

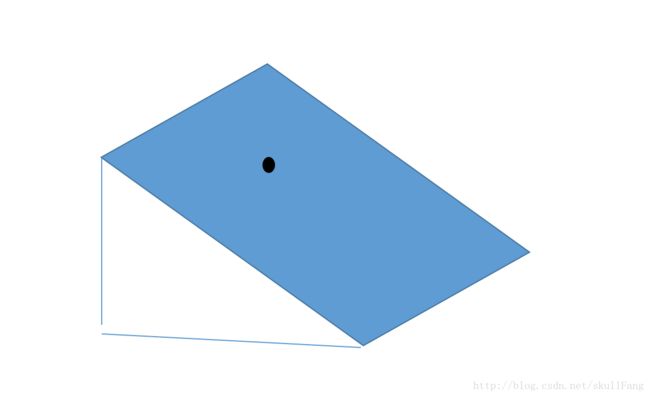
我们如果想要它顺利到碗底，按照我们一元凸函数的理论可以在这个维度上找到挪动的方向，这个是二维的。我们可以理解为需要挪动两次。
（水平一次）（竖直一次）
也就是


这两个方向。类似与

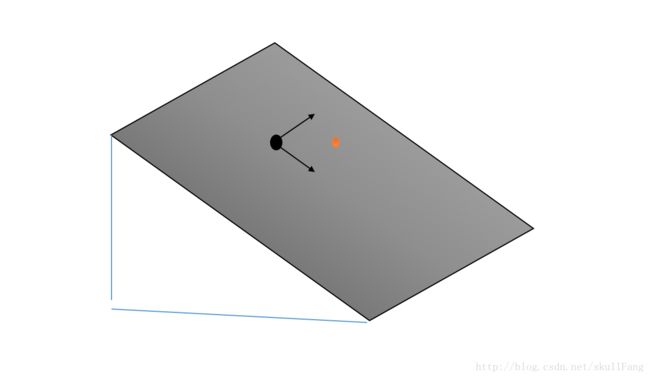
那么为啥要一步一步挪呢？直接按照斜线下去不久更快么？

没错。到这里就开始上路了。于是就搞了一个梯度的概念。

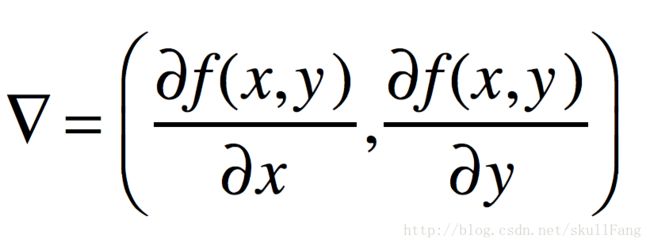
然后我们每次更新就用相对应地维度去减这个梯度好啦。这个梯度可以是n维的。

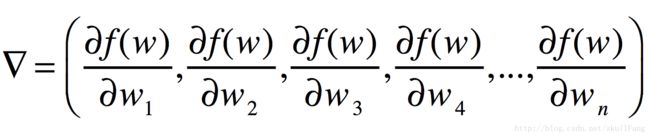
那么更新公式就是

也就是说参数的更新就是当前值减去梯度。

模型构建

我们还是从多层感知机看起。
假设我们每一层只有一个神经元，只要把这个做出来其他都是一样的。（这个层的神经元多，了只不过是多维度基本代码不会变）。

根据前向传播原理
从隐藏层开始算

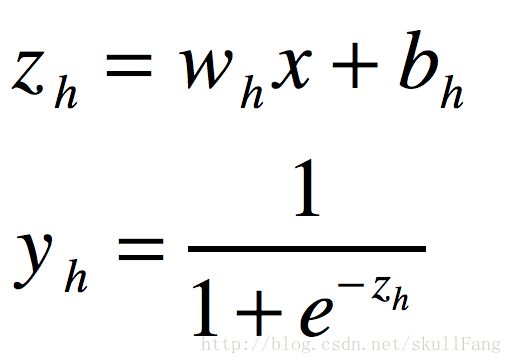
隐藏层到输出层

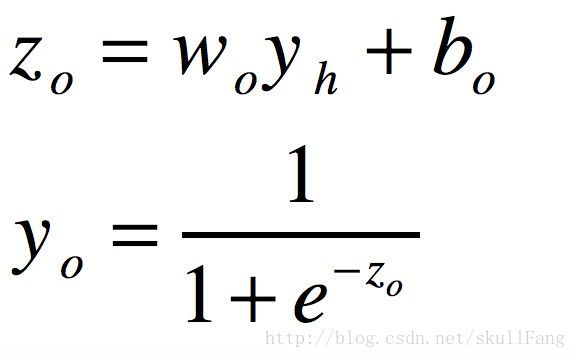
根据我们损失函数定义

为了求导方便Loss前面加一个常数项

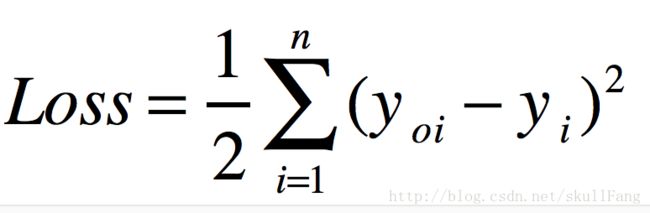
根据反向传播原理我们需要更新
wh,bh, wo,bo的值。
由梯度下降算法可知，于是有了四个表达式

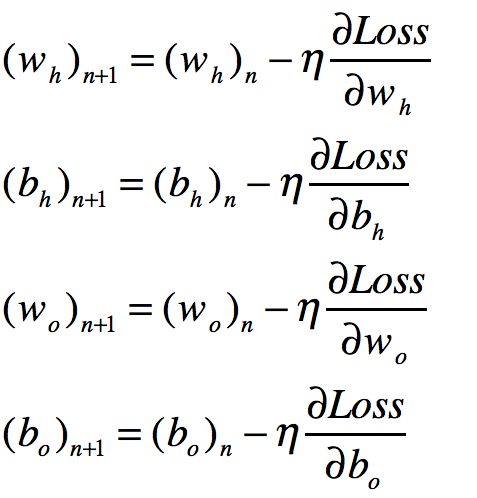
其中的wh,bh,wo,bo是我们已经知道的值。而wh+1,bh+1,wo+1,bo+1是我们需要更新的值。因为wh,bh,wo,bo已经确定，所以只要我们求出。Loss 对每个待定系数的偏导数。

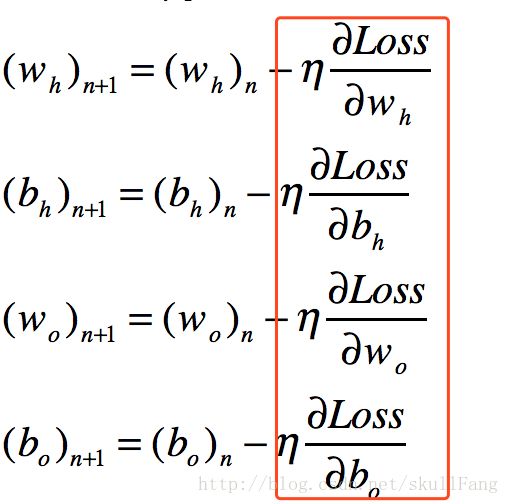
因为是反向传播，我们需先看输出层的wo和bo.
根据公式和求导链式法则（）

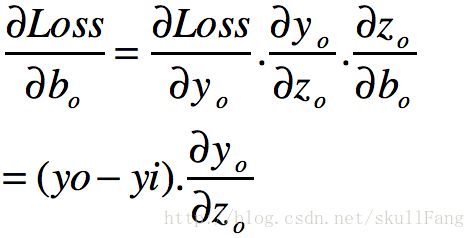
因为

这个导数又个特性就是。
图片
于是就有了

同理

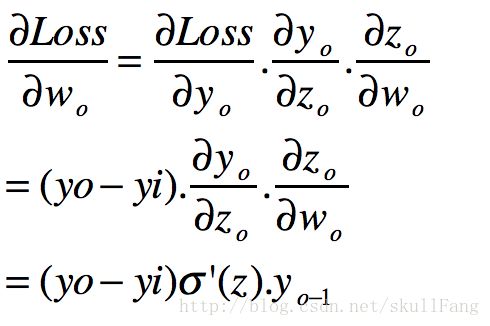
那么我们可以定意一个新的变量。

OK 解决了最后一层
再看隐藏层，因为隐藏层可能有很多，我们要找到一个反向传递的公式出来。也是根据求导的链式法则的。首先看看。

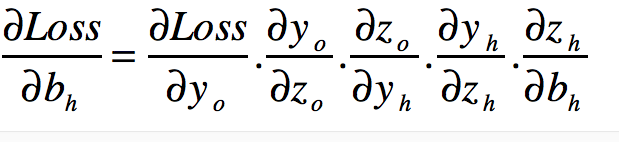
很长，但是一定要知道为什么。为什么呢？就是求导的链式法则。一层一层的把它剥开。

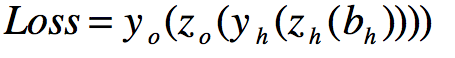
我们很快可以求出导数

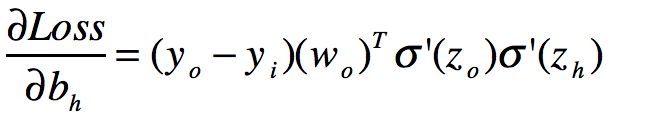
觉得头晕的兄弟可以自己推一下很快的。

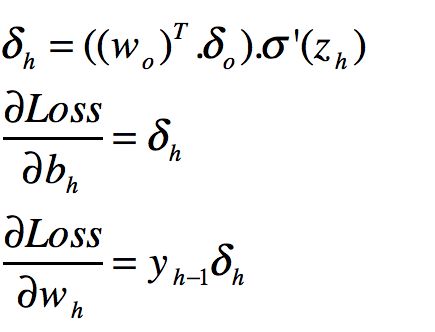
我们还是整理一下。

我们在这一步发现了一个很重要的信息。
就是如果你想知道当前层的偏b和偏w，必须知道下一层的信息。这也就是为什么是反向传播的原因。

公式有点多，请大家谅解。可以自己推一下不难的。

算法设计

前向传播在上一文中已经实现了。本文就实现出反向传播。

1、计算最后一层的delta
由公式推导可以知道，我们想求出最后一层的delta必须知道yo的值和zo的值。

我们要知道当前层的z
我们要知道当前层的y
我们要知道上一层的y

于是我们吧所有的层产生的y和z保存到两个列表里面。

2、计算出最后一层的权重和偏置的偏导数

3、计算所有隐藏层到第一层权重和偏置的偏导数。（反向更新）

我们要知道当前层的Z
我们要知道下一层的w
我们要知道下一层的delta
我们要知道前一层的y
按照公式来。

利用两个列表进行操作。每一层更新自己的delta供上一层用。这个delta就是在传递。从最后一层传到第一层。这就是反向传播。

代码部分

# -*- coding: utf-8 -*-
# @Time    : 2017/11/24 下午2:34
# @Author  : SkullFang
# @Email   : [email protected]
# @File    : MnistDemo.py
# @Software: PyCharm
import random
import numpy as np
class NetWork(object):
    def __init__(self,sizes):
        """
        初始化
        :param sizes: 
        """
        self.num_layers=len(sizes)
        self.sizes=sizes
        #偏置
        self.biases=[np.random.randn(y,1)
                     for y in sizes[1:]]
        #权重

        self.weights=[np.random.randn(y,x)
                      for x,y in zip(sizes[:-1],sizes[1:])]

    def GD(self,training_data,epochs,eta):
        """
        梯度下降
        :param training_data: 训练数据
        :param epochs: 训练次数
        :param eta: 学习率
        :return: 
        """
        for j in xrange(epochs):
            random.shuffle(training_data)

            # 保存每层偏倒
            nabla_b = [np.zeros(b.shape) for b in self.biases]
            nabla_w = [np.zeros(w.shape) for w in self.weights]

            for x,y in training_data:
                delta_nable_b, delta_nabla_w = self.update(x, y)

                # 保存一次训练网络中每层的偏倒
                nabla_b = [nb + dnb for nb, dnb in zip(nabla_b, delta_nable_b)]
                nabla_w = [nw + dnw for nw, dnw in zip(nabla_w, delta_nabla_w)]

            self.weights=[w-(eta)*nw
                          for w,nw in zip(self.weights,nabla_w)]

            self.biases=[b-(eta)*nb for b,nb in zip(self.biases,nabla_b)]


            print "Epoch {0} complete".format(j)

    def update(self,x,y):
        """
        正向传播和反向传播
        :param x: 
        :param y: 
        :return: 
        """

        # 初始化一个矩阵用于保存每层偏导
        nabla_b = [np.zeros(b.shape) for b in self.biases]
        nabla_w = [np.zeros(w.shape) for w in self.weights]
        #输入层
        activation=x

        #保存每一层的激励值
        activations=[x]

        #保存每一层的z=wx+b
        zs=[]

        for b,w in zip(self.biases,self.weights):

            #重复更新activation
            z=np.dot(w,activation)+b

            zs.append(z)

            activation=sigmoid(z)

            activations.append(activation)

        #计算最后一层 的delta
        delta=self.cost_derivative(activations[-1],y)*sigmoid_prime(zs[-1])

        #计算最后一层的的权重和偏置的偏导数
        nabla_b[-1]=delta
        nabla_w[-1]=np.dot(delta,activations[-2].transpose())

        #计算倒数第二层到第一层的权重和偏置的偏导数
        for l in range(2,self.num_layers):
            #当前层的z
            z=zs[-l]
            #自己层的偏导
            sp=sigmoid_prime(z)
            #自己层的delta 按照公式来。每次更新delta 供上一层用。
            delta=np.dot(self.weights[-l+1].transpose(),delta)*sp
            #当前层的偏置
            nabla_b[-l]=delta
            nabla_w[-l]=np.dot(delta,activations[-l-1].transpose())


        return (nabla_b,nabla_w)

    def cost_derivative(self, output_activation, y):
        """
        计算y-yi
        :param output_activation: 
        :param y: 
        :return: 
        """
        return (output_activation - y)


def sigmoid_prime(z):
    """
    sigmoid的偏导数
    :param z: 
    :return: 
    """
    return sigmoid(z)*(1-sigmoid(z))


def sigmoid(z):
    """
    激励函数
    :param z: 
    :return: 
    """
    return 1.0/(1.0+np.exp(-z))