神经网络之梯度下降与反向传播（上）

一、概述

对于一个函数，希望找到使函数值达到全局最小的自变量值。这是优化理论研究的问题。梯度下降法是一种基于函数一阶性质的优化算法。人工神经网络的训练主要采用梯度下降法，其计算过程中采用误差反向传播的方式计算误差函数对全部权值和偏置值的梯度。本文首先介绍梯度下降法，下篇将介绍反向传播算法并实现一个全连接神经网络。

首先用语言来描述几个概念。这里的描述尽量抓重点，但是不够精确。精确的概念只能用公式把握，在下文中都有阐述。

• 仿射函数：仿射函数是线性函数。仿射函数的图形是空间中一个平面。
• 函数可导：若函数在某一点可导，则函数在这一点附近可用一个仿射函数很好地近似。该仿射函数的图形（平面），就是函数在这一点的切平面。
• 梯度：函数在某一点的梯度是一个自变量空间内的向量。自变量顺着梯度方向变化时函数值上升得最快。梯度的模（长度）是函数值上升的速率。梯度朝某方向投影的长度是自变量顺着该方向变化时函数值的变化率。
• 梯度下降：一种优化算法，该算法从任一点开始，沿该点梯度的反方向运动一段距离，再沿新位置的梯度反方向运行一段距离 ...... 如此迭代。解一直朝下坡最陡的方向运动，希望能运动到函数的全局最小点。

下文中都以二元函数为例。因为二元函数的自变量空间是 xy 平面，函数图形所在空间是三维空间，便于可视化。其它维度可以类推。

二、仿射函数

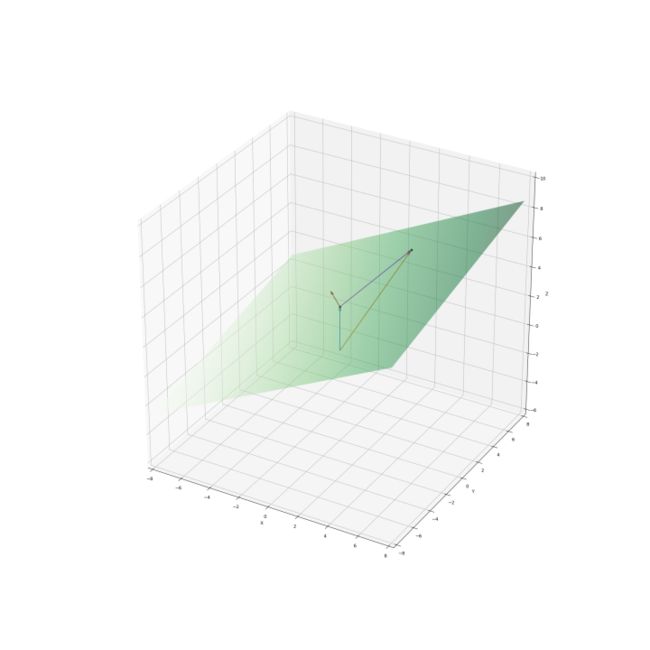
仿射函数的图形是一个平面。如图 1 。

图 1 ——仿射函数图形（平面）

该平面的方程是：

该平面的截距是 3 。当 (x, y) 取 (0, 0) 时 z 的值为 3 ，即平面与 z 轴相交于 (0, 0, 3) 。将该方程变形：

所有平面上的点都满足式 2.1（或式 2.2 ）。式 2.2 中的 (-0.5, -0.2, 1) 是该平面的法向量（图 1 中的红色箭头）。该平面上的线段是它的两个端点向量 (x1, y1, z1) 和 (x2, y2, z2) 之差 (x2-x1, y2-y1, z2-z1) 。因为 (x1, y1, z1) 和 (x2, y2, z2) 都在该平面上，所以这个线段与法向量 (-0.5, -0.2, 1) 正交：

例如，图 1 中两个黑色圆点都在平面上，其坐标分别是 (0, 0, 3) 和 (2, 5, 5) 。蓝色箭头和黄色箭头分别是它们对应的向量。紫色箭头是这两个向量之差 (2, 5, 2)。该差向量经过平移就是平面上的一个线段。 (2, 5, 2) 与法向量 (-0.5, -0.2, 1) 内积为 0 ，即它们正交。平面上所有线段都与法向量正交， 即法向量垂直于该平面。法向量指示一个方向。该方向确定了平面的倾向和倾角。法向量的长度（模）不重要。如果将式 2.2 两端同时乘以 2 ，法向量长了一倍，但平面没有变化：

虽然常量项从 3 变成了 6 ，但由于 z 的系数变成了 2 ，故平面的截距仍是 3 。如果法向量第三个分量为 0 ，则平面是竖直的。例如式 2.5 ：

式 2.5 要求 x 和 y 满足 -2x-3y=3 ，z 值任意。它确定的是一个竖直平面。如果平面非竖直，则总可以通过缩放使 z 的系数为 1 。于是非竖直平面的法向量总可以写成 (a1, a2, 1) 的形式。第三分量保持为 1 的前提下，a1 和 a2 的绝对值越大，法向量越靠近 xy 面，平面也就被“撬起”得越高；反之 a1 和 a2 的绝对值越小，法向量越接近竖直，平面被 “放躺” 得越平。想象把法向量当作一个把手来回扳动，平面也就可以随意调整朝向。

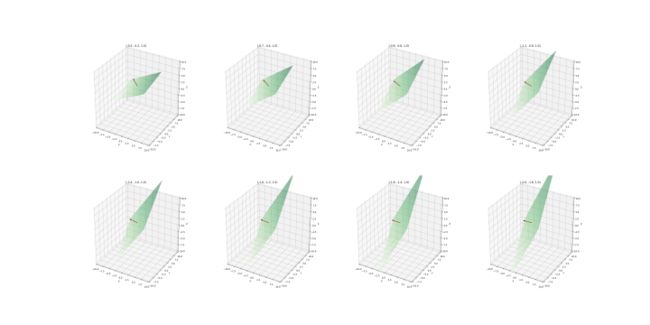
图 2 展示了 8 个法向量不同的平面。子图标题是每个平面的法向量。图中红色箭头指示了法向量的方向，但其长度没有反映法向量的模。注意随着 a1 和 a2 绝对值的不同，平面陡峭程度的变化。

图 2 ——法向量不同的平面

脱离具体数值，仿射函数的方程形式为：

式 2.6 等价于：

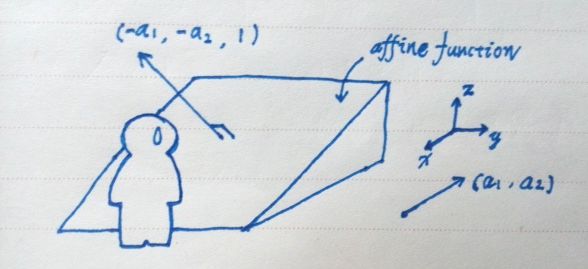
全体满足式 2.6（或 2.7）的点 (x, y, z) 构成三维空间中一个非竖直的平面。(a1, a2) 决定了平面的倾向和倾角。b 称截距。平面于 z 轴相交于 (0, 0, b) 。b 决定了平面位置的高低。(-a1, -a2, 1) 是该平面的法向量，法向量垂直于平面。a1 和 a2 的绝对值越大，法向量越接近水平，平面就被撬得越陡峭。 (-a1, -a2) 作为 xy 面内的向量决定了平面的倾向，也就是下坡的方向。相反的 (a1, a2) 是上坡的方向。下一节将会提到：函数 f 在某点可导，则 f 可在这一点被一个仿射函数（平面）很好地近似。该近似平面爬坡最陡的 (a1, a2) 方向就是 f 在该点上升最快的方向，即 f 在这一点的梯度。参考图 3 。

图 3 ——梯度方向坡最陡

三、导数和梯度

对于函数，在某个点 (x0, y0) 附近找到一个仿射函数去近似它 ：

一个好的近似，首先要求该仿射函数在 (x0, y0) 与 f 是相等：

截距 b 由此确定：

将 b 代回式 3.1 ，近似式可重写为：

通过引入一个余项 R ，成为 = 。R 是仿射函数与 f 的差，在 (x0, y0) 为 0 。好的近似要求 R 随着 (x, y) 接近 (x0, y0) 而减小至消失，且减小得比 (x, y) 接近 (x0, y0) 的速度更快。用数学语言来表述，就是要求：

||(x, y)-(x0, y0)|| 是 (x, y) 与 (x0, y0) 的差的模，即它们之间的距离。式 3.5 表示余项 R 是 (x, y) 与 (x0, y0) 之间距离的高阶无穷小：随着 (x, y) 与 (x0, y0) 之间的距离趋近于 0 ，R 与该距离的比值也趋近于 0 。 R 减小得比 (x, y) 接近 (x0, y0) 更快：

小结一下。在 (x0, y0) 想用一个仿射函数（平面）去近似代表 f 。在 (x0, y0) 上该仿射函数和 f 相等。在其他位置或有差距，但这个差距随着靠近 (x0, y0) 而减小至消失，且减小得比靠近 (x0, y0) 的速度更快。

这样的近似仿射函数在 f 的某一点 (x0, y0) 如果存在，则是唯一的。如果在 (x0, y0) 存在这样的近似仿射函数，就说 f 在 (x0, y0) 可导。该仿射函数是 f 在 (x0, y0) 的一阶近似。仿射函数的图形（平面）是 f 在 (x0, y0) 的切平面。

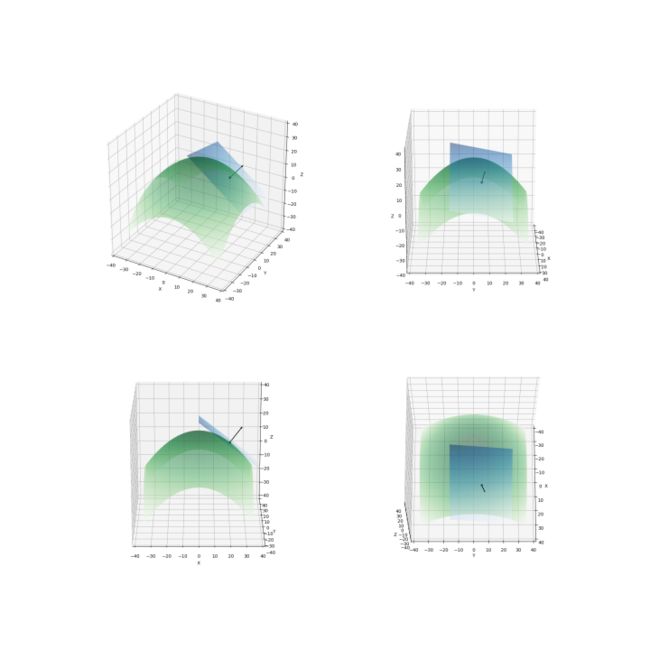
如图 4 ，绿色曲面为函数。蓝色平面为该函数在 (20, 5) 处的切平面 z=-0.8x-0.2y+28.5 。切平面的法向量是 (-0.8, -0.2, 1)，其方向如图中倾斜箭头所示（箭头的长度不等于法向量的模，为了看得清楚而拉长了）。

图 4 ——二次曲面在 (1,1) 的切平面（四种角度）

如果是某个非零向量 ，根据式 3.4、式 3.5 和式 3.6 可得到：

最左侧是 f 在 (x0, y0) 点沿着方向的方向导数。也就是自变量沿着该方向变化时 f 的变化速率。f 在不同的方向上变化速率不同，其值是 (a1, a2) 在方向上的投影：

是 (a1, a2) 与之间的夹角。可见自变量变化方向与 (a1, a2) 相同时，函数变化速率最大（>0）；自变量变化方向与 (a1, a2) 相反时，函数变化速率最小（<0）；自变量变化方向与 (a1, a2) 垂直时，函数变化速率为 0 。(a1, a2) 就是 f 在 (x0, y0) 的梯度。梯度投影到某个方向的长度就是 f 沿该方向的变化速率。为了确定梯度的取值，计算 f 在 (x0, y0) 沿 (1, 0) 的方向导数，即 f 在 (x0, y0) 对 x 的偏导数：

即梯度的第一个元素是 f 在 (x0, y0) 对 x 的偏导数。同样，梯度的第二个元素是 f 在 (x0, y0) 对 y 的偏导数。于是 f 在 (x0, y0) 的梯度就是：

小结一下。可导函数在任一点的梯度是自变量空间中的一个向量（二元函数的梯度是 xy 平面上的向量，而不是 xyz 空间里的向量）。函数图形在这一点的切平面的法向量投影在自变量空间中，就是该点梯度的反方向。某点的梯度是函数以及它的切平面在该点上升最快的方向，即方向导数最大的方向。梯度的长度（模）就是在该方向的方向导数（变化率）。梯度向任何自变量空间方向的投影的长度（模）是函数在该方向上的方向导数（变化率）。梯度可以是 0 向量。在梯度为 0 向量的点上各方向的变化率都为 0 。这是函数达到极大／极小值的一阶必要非充分条件（例如鞍点不是极大／极小值，但是梯度也为 0 ）。

四、梯度下降

想像你于伸手不见五指的黑夜身处一座地形复杂的山中。你看不清山的全貌，只能根据重力感知立足之处的坡度。如果想要下山，你该怎么做？你根据此处的重力感觉，向下坡最陡的方向迈一步。然后根据新位置的坡度，再向下坡最陡的方向迈出下一步。如果来到一个位置，你感觉已经站在了平地上，再没有下坡的方向，你也就无从迈出下一步了。此时你可能已经成功到达海拔最低的山底，但也有可能身处半山腰处一块平地或者一个盆地底部。

这就是梯度下降法的形象描述。山就是三维空间中函数的图形。某个位置下坡最陡的前进方向就是函数在该点梯度的反方向。向前迈一步，就是让自变量沿着梯度反方向运动一个距离（步长）。感觉已站在平地，就是当前点的梯度为 0 。梯度下降算法的迭代公式为：

(x0, y0) 为随机的初始点。为步长。考虑一个具体例子。“香蕉函数”的方程是：

图 5 ——香蕉函数图形（多角度）

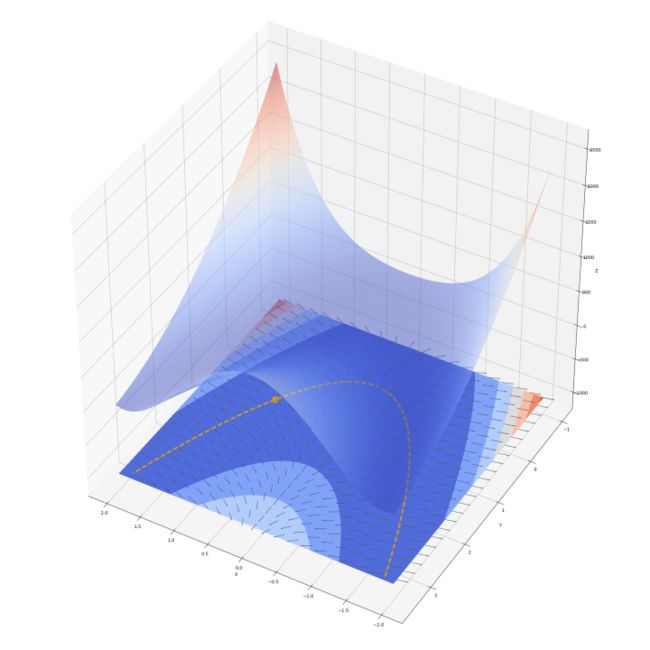
图 5 是香蕉函数的图形。之所以被称为香蕉函数，是因为该函数的等高线图形状像香蕉。香蕉函数的全局最小点在 (1, 1) （图 5 左上角图中红点）。香蕉函数的梯度为：

图 6 ——香蕉函数梯度场、驻点以及梯度平缓峡谷

图 6 展示了香蕉函数的梯度场。注意图中小箭头仅指示该点梯度方向，其长度并不反映梯度大小。从式 4.3 可以计算得出，香蕉函数梯度为 (0, 0) 的点是 (1, 1) 。在 二次曲线上，梯度的 y 分量为 0 ，梯度的 x 分量为 2(x-1) 。

在二次曲线 上（图 6 黄色曲线），若 x>1 ，则梯度 x 分量大于 0 ，曲面向正 x 方向上坡；反之若 x<1 ，梯度 x 分量小于 0，曲面向 -x 方向上坡。x 离 1 越远则坡越陡。x 为 1 时梯度 x 分量为 0 ，梯度是 (0, 0) ，各个方向都不上下坡。(0, 0) 是曲面的驻点（图 6 中黄色圆点）。曲面在 (0, 0) 取得最小值 0 。以下把 称作二次曲线峡谷。

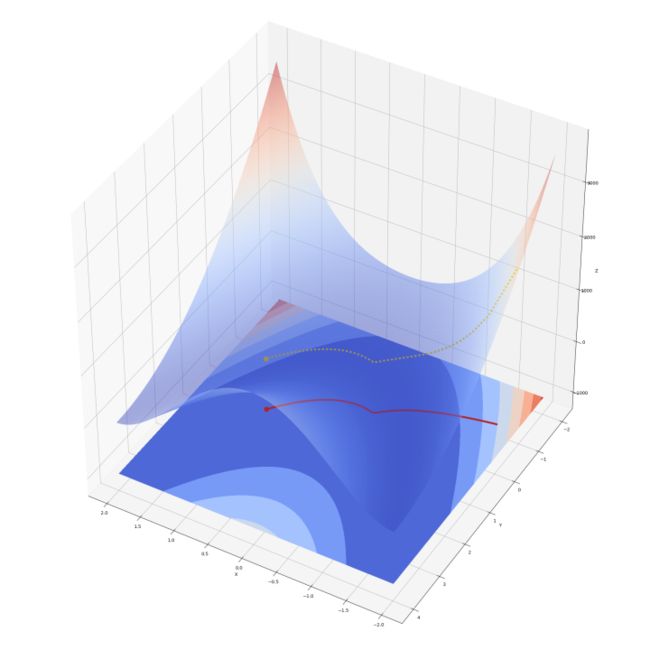
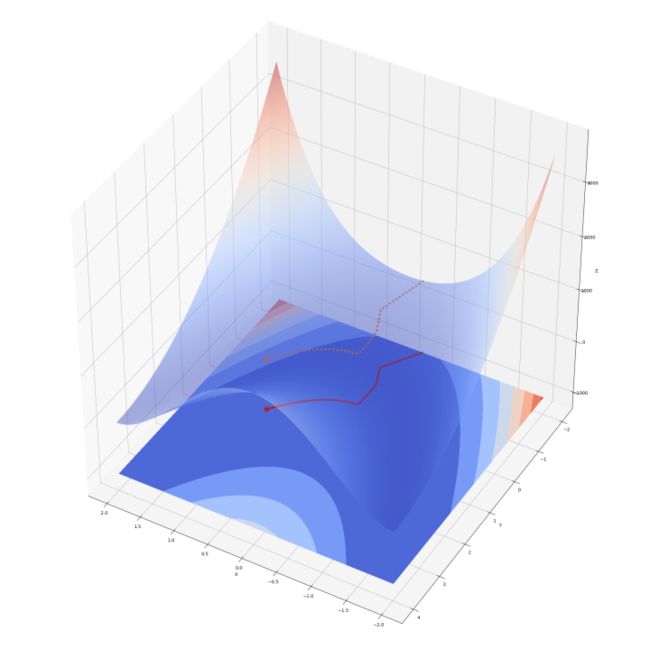
在香蕉函数上运行梯度下降法。以 (-1.9 -0.9) 为初始点。以 0.0001 为步长。当梯度长度（模）小于 1e-4 时停止。梯度下降算法运行结果如图 7 所示。

图 7 ——香蕉函数上的梯度下降（ 0.0001 步长）

算法共迭代 199078 步。最终停止在 (0.9999, 0.9998) ，很接近 (1, 1) 。可认为算法成功找到了最优点。图 7 中红色线是解的运动轨迹，红点是最终位置。黄色虚线显示函数值随着迭代下降。解进入二次曲线峡谷时有一个明显的转向，之后沿着峡谷向最优点前进。如果增大步长，算法会收敛得更快。下面以 0.0009 为步长实验一下。结果如图 8 。

图 8 ——香蕉函数上的梯度下降（ 0.0011 步长）

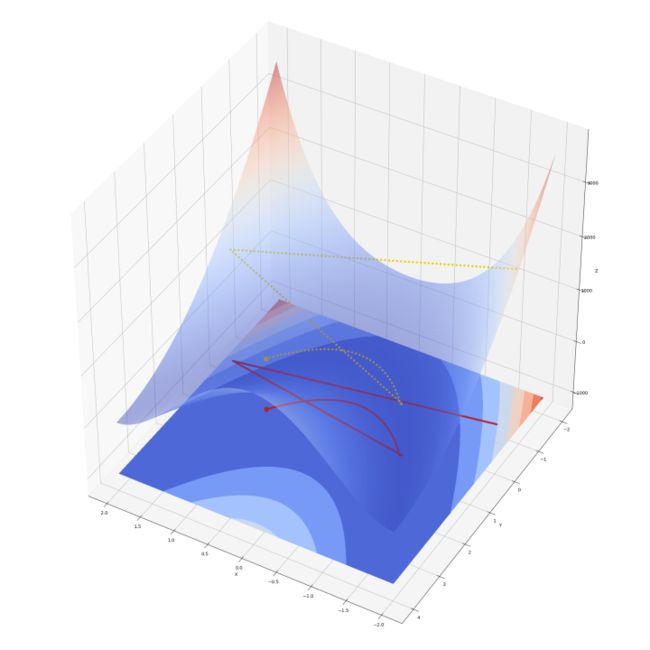
停止点仍是 (0.9999, 0.9998) ，步数为 18567 步，收敛速度加快了 10 倍。可以看到在梯度较大的地方由于运动距离大，解一下跳过了二次曲线峡谷而冲上了对面山坡。经过两大步的调整后解进入了峡谷，开始向目标缓慢前进。接下来换一个出发点。出发点选择在 (-1.0, -2.0) 。这里的梯度没有 (-1.9, -0.9) 大。步长选择较大的 0.007 。运行效果如图 9 。迭代了 9890 步，停止在 (0.9999, 0.9998) 。

图 9 ——香蕉函数上的梯度下降（另一个起点，0.007 步长）

步长的选择学问很多。若步长过短，则算法收敛慢。若步长太长，则有可能一下冲过谷底，或者发生震荡，难以精确收敛到最优解。步长显然应该与待优化函数自变量本身的尺度有关。一般来讲步长应该随着算法迭代而调整。办法包括但不限于：

• 随着迭代进行而衰减。算法开始时采用较大的步长，随着解接近最优解，逐步缩小步长，在最优解周围细致搜索；
• 根据梯度选择步长。梯度小的地方函数平坦，采用较大步长快速跨过平坦区。梯度大的地方函数变化剧烈，采用较小步长以免“冲过头”；

梯度下降法算法何时停止？梯度为 0 的点满足极小点的一阶必要条件，是全局最小点的候选点。找到这样的点算法就“走不动”了——解不再更新。但是由于步长或计算机浮点数精度所限，解基本上不可能运动到梯度精确为 0 的点。可以设置一个阈值，例如上例中采用 1e-4 。若当前点的梯度的模小于阈值，则认为该点梯度近似为 0 ，算法停止。由于步长不合适，算法可能在最优点周围来回震荡而无法停止。可以通过设置最大迭代次数来避免这种情况。

梯度下降算法只利用了目标函数的一阶特性。最好情况无非是找到梯度为 0 的点（驻点）。梯度为 0 是全局最小点的必要非充分条件。它有可能根本不是极小点（是鞍点），也有可能是局部极小点。陷入局部极小点是梯度下降法的一大问题。可以从多个不同的初始点尝试多次运行算法。还可以加入“冲量”（momentum）。加入冲量的更新式是：

通过一个 0 与 1 之间的因子，将上一次的前进方向混合进本次前进方向。就好像有了一个惯性。冲量有助于缓解震荡以及防止陷入局部极小点。

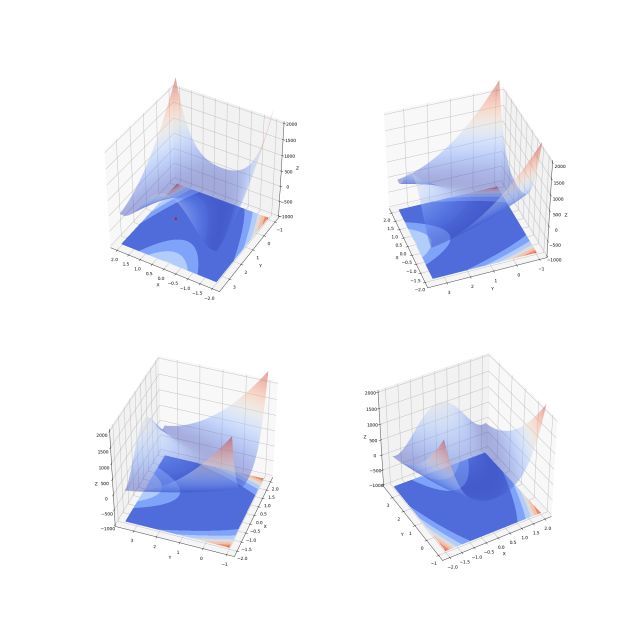
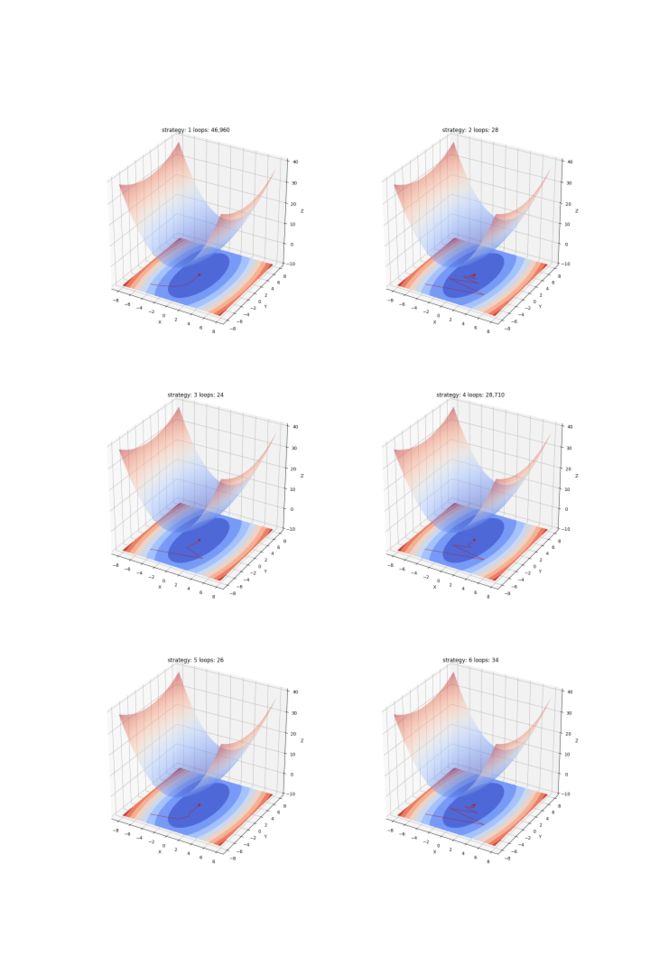
图 10 展示了在 6 种不同更新策略下梯度下降法在二次曲面 上的运行情况。每个子图的标题中有迭代次数。每种策略的说明和实现参见文末代码。

图 10 ——在二次曲面上实验 6 种更新策略

五、例举：线性回归

求线性回归的最小二乘解涉及矩阵求逆。在样本量大／维度高的情况下计算量较大。这时可以使用梯度下降法近似来求最小二乘解。寻找关于回归直线斜率 a 和截距 b 的误差函数 e 的全局最小点（最小二乘解就是 e 的全局最小点，通过解析地求梯度为 0 点而得到）：

(xi, yi) 为待拟合的样本点，共 n 个。e 在 (a, b) 的梯度是：

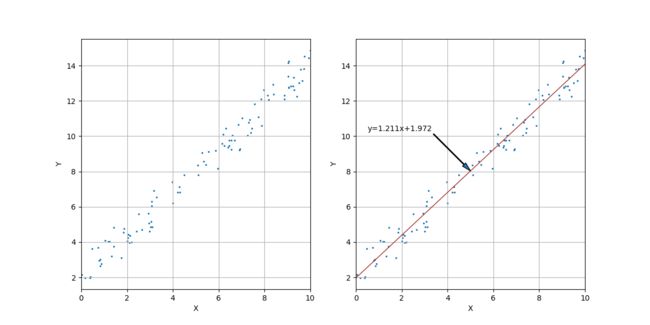
实验一下。生成 100 个直线 y=1.2x+2.0 上的点。对每个点的 y 值加上均值为 0 ，标准差为 0.6 的正态噪声。如图 11 。

图 11 ——围绕直线的有噪声点以及最小二乘线性回归直线

图 11 左侧为 100 个样本点，右侧显示了用最小二乘法求得的线性回归直线。如图中标注，回归直线的方程是 y=1.211x+1.972 ，比较准确。(1.211, 1.972) 就是 e 的全局最小点，也是梯度下降法所要寻找的目标点。

图 12 ——梯度下降法寻找最小二乘解

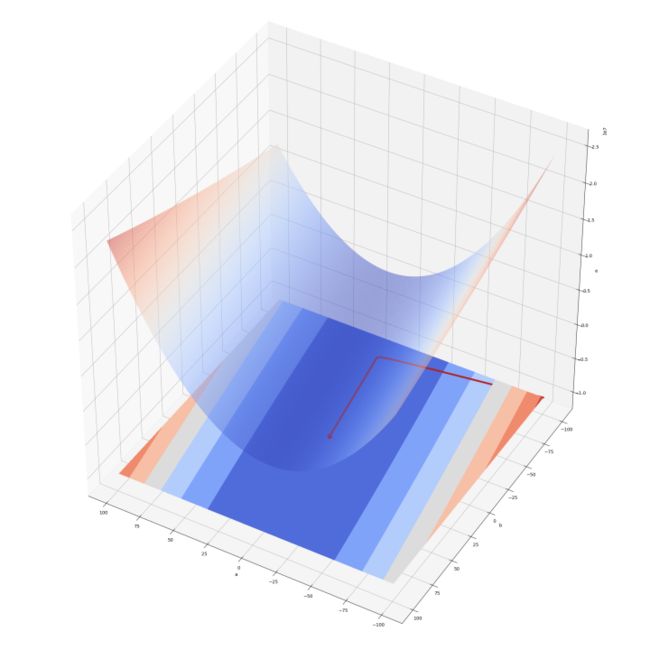
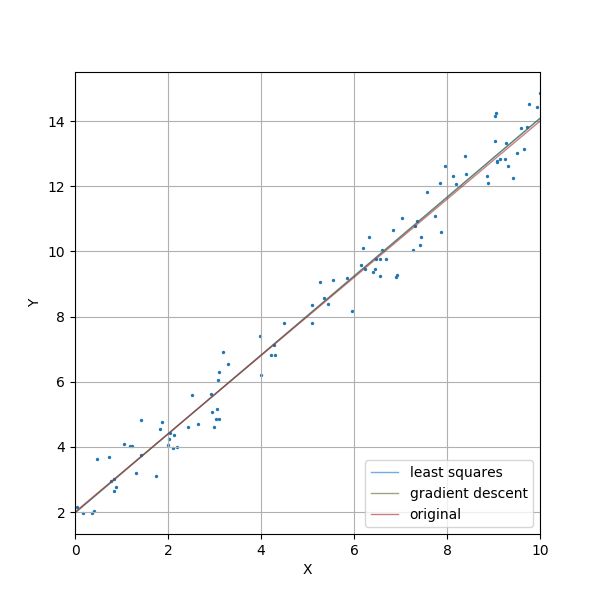
图 12 中的曲面是以直线斜率 a 和截距 b 为自变量的误差 e 曲面。梯度下降算法起始点为 (-100, -100) 。步长为 0.0001 。梯度模停止阈值为 1e-4 。迭代共进行了 6789 步。红线是解的运行路径。红点是最终点。红点的坐标是 (1.2112, 1.9725) 。忽略舍入误差，梯度下降算法成功找到了最小二乘解。图 13 显示了 100 个样本点、直线 y=1.2x+2.0 、最小二乘回归直线 y=1.211x+1.972 以及运用梯度下降找到的直线 y=1.2112x+1.9725 。

图 13 ——随机点、最小二乘法求得的回归直线以及梯度下降法找到的直线

六、结语

梯度下降法的本质是在某个位置将目标函数一阶展开，利用其一阶性质持续向函数值下降最快的方向前进，以期找到函数的全局最小解。梯度下降属于梯度优化方法大类，此外还有最速下降法，共轭梯度法等等。还有其他方法基于目标函数的二阶性质，比如牛顿法、拟牛顿法等。

用来训练神经网络的反向传播算法是梯度下降法。不过它需要求得误差函数对众多权重和偏置值的偏导数。反向传播法在前向计算网络输出的过程中把一些“局部误差”反向传播。借助这些局部误差计算误差函数对每个权重和偏置值的偏导数，得到梯度。下一篇专栏中将详细介绍反向传播算法。

最后附上本文代码。

import numpy as np
import matplotlib.pyplot as plt
from matplotlib import cm
from mpl_toolkits.mplot3d import Axes3D


def quadratic(x, y):
    return 0.5 * x ** 2 + 0.1 * y ** 2


def quadratic_grad(x, y):
    return np.array([x, 0.2 * y])


max_eta = 1.66
min_eta = 0.001


def strategy1(grad, last_grad, iters):
    """
    固定步长 min_eta 。
    """
    global max_eta, min_eta
    eta = min_eta
    return -eta * grad


def strategy2(grad, last_grad, iters):
    """
    固定步长 max_eta 。
    """
    global max_eta, min_eta
    return -max_eta * grad


def strategy3(grad, last_grad, iters):
    """
    固定步长 max_eta ，以 0.1 为系数加入冲量。
    """
    global max_eta, min_eta
    return -max_eta * ((1 - 0.1) * grad + 0.1 * last_grad)


def strategy4(grad, last_grad, iters):
    """
    初始步长为 max_eta ，以 0.9 为衰减因子衰减步长。保障步长大于等于 min_eta 。
    """
    global max_eta, min_eta

    if not iters:
        eta = max_eta
    else:
        eta = min_eta if max_eta * 0.9 ** iters <= min_eta else max_eta * 0.9 ** iters

    return -eta * grad


def strategy5(grad, last_grad, iters):
    """
    根据梯度的大小。在梯度大的地方减小步长，在梯度小的地方增加步长。保障步长大于等于 min_eta 。
    具体计算方法是：步长＝max_eta / e^(magnitude/10.0) 。
    e 是自然对数的底，magnitude 是当前梯度的长度。
    """
    global max_eta, min_eta

    magnitude = np.sqrt(np.dot(grad, grad))
    coe = np.power(np.e, magnitude / 10.0)
    if coe > 0:
        eta = max_eta / coe
    else:
        eta = min_eta

    eta = min_eta if eta <= min_eta else eta
    return -eta * grad


def strategy6(grad, last_grad, iters):
    """
    根据当前梯度与上一位置的梯度交角调整步长。
    交角大，认为地形崎岖变化大，缩小步长。若交角小，认为地形变化不大，增大步长。
    具体步长公式为：步长 = max_eta * (cos_theta ＋ 1.0001) / 2.0001 。
    cos_theta 是本次梯度与上一次梯度的交角余弦值。加上 1.0001 是将系数调整为正数。
    """
    global max_eta, min_eta

    l_grad = np.sqrt(np.dot(grad, grad))
    l_last_grad = np.sqrt(np.dot(last_grad, last_grad))

    if l_grad > 0 and l_last_grad > 0:
        cos_theta = np.dot(grad, last_grad) / (l_grad * l_last_grad)
        eta = max_eta * (cos_theta + 1.001) / 2.0001
    else:
        eta = max_eta

    eta = min_eta if eta <= min_eta else eta
    return -eta * grad


def draw_chart(fun, path, ax):
    x, y = np.meshgrid(np.arange(-8.0, 8.0, 0.1), np.arange(-8.0, 8.0, 0.1))
    z = fun(x, y)

    ax.plot_surface(x, y, z, rstride=1, cstride=1, alpha=0.5, cmap=cm.coolwarm)
    ax.contourf(x, y, z, zdir='z', offset=-10.0, cmap=cm.coolwarm)

    ax.set_xlabel('X')
    ax.set_ylabel('Y')
    ax.set_zlabel('Z')
    ax.set_zlim([-10.0, 40.0])

    if path is not None:
        ax.plot(path[0], path[1], [-10.0] * len(path[0]), c="#b22222", linewidth=0.8)
        ax.scatter(path[0][-1], path[1][-1], [-10.0], c="#b22222")


def gradient_descent(init_position, gradient_fun, step_fun, tolerance=1e-4, max_iters=None):
    x = [init_position[0]]
    y = [init_position[1]]
    iters = 0
    last_grad = np.array([0.0, 0.0])

    while True:
        cx = x[-1]
        cy = y[-1]

        grad = gradient_fun(cx, cy)
        step = step_fun(grad, last_grad, iters)

        x.append(cx + step[0])
        y.append(cy + step[1])

        last_grad = grad
        iters += 1
        magnitude = np.sqrt(np.dot(grad, grad))

        if magnitude < tolerance or (max_iters is not None and iters >= max_iters):
            break

    return {"final_pos": [x[-1], y[-1]], "iters": iters, "final_grad": grad, "path": [x, y]}


fig = plt.figure(figsize=(20, 30))

strategies = [strategy1, strategy2, strategy3, strategy4, strategy5, strategy6]

for step_func, index in zip(strategies, np.arange(1, len(strategies) + 1)):
    ax = fig.add_subplot(3, 2, index, projection="3d")
    result = gradient_descent([-6.0, -6.0], quadratic_grad, step_func)
    draw_chart(quadratic, result["path"], ax)
    ax.set_title("strategy: {:d} loops: {:,}".format(index, result["iters"]))
    print("running strategy {:d}".format(index))

plt.savefig("strategies.png")
plt.cla()
plt.clf()
plt.close()

七、参考书目

[1] 《最优化导论》（美）Edwin K. P. Chong（美） Stanislaw H. Zak