leetcode-96-不同的二叉搜索树-java

题目及测试

package pid096;
/*96. 不同的二叉搜索树

给定一个整数 n，求以 1 ... n 为节点组成的二叉搜索树有多少种？

示例:

输入: 3
输出: 5
解释:
给定 n = 3, 一共有 5 种不同结构的二叉搜索树:

   1         3     3      2      1
    \       /     /      / \      \
     3     2     1      1   3      2
    /     /       \                 \
   2     1         2                 3


*/
public class main {
	
	public static void main(String[] args) {
		int[] testTable = {3,4};
		for (int i=0;i

解法1（0ms，极快）

给定一个有序序列 1⋯n，为了构建出一棵二叉搜索树，我们可以遍历每个数字 i，将该数字作为树根，将 1⋯(i−1)序列作为左子树，将 (i+1)⋯n 序列作为右子树。接着我们可以按照同样的方式递归构建左子树和右子树。

在上述构建的过程中，由于根的值不同，因此我们能保证每棵二叉搜索树是唯一的。

由此可见，原问题可以分解成规模较小的两个子问题，且子问题的解可以复用。因此，我们可以想到使用动态规划来求解本题。

题目要求是计算不同二叉搜索树的个数。为此，我们可以定义两个函数：

G(n): 长度为 n 的序列能构成的不同二叉搜索树的个数。

F(i,n): 以 i 为根、序列长度为 n 的不同二叉搜索树个数 (1≤i≤n)。

可见，G(n) 是我们求解需要的函数。

稍后我们将看到，G(n) 可以从 F(i,n) 得到，而 F(i,n) 又会递归地依赖于 G(n)。

首先，根据上一节中的思路，不同的二叉搜索树的总数 G(n)，是对遍历所有 i (1≤i≤n) 的 F(i,n) 之和。换言之：

G(n)=∑i=1-n F(i,n)

对于边界情况，当序列长度为 1（只有根）或为 0（空树）时，只有一种情况，即：

G(0)=1,G(1)=1

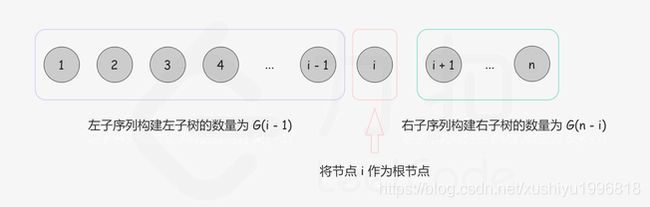
给定序列 1⋯n，我们选择数字 i 作为根，则根为 i 的所有二叉搜索树的集合是左子树集合和右子树集合的笛卡尔积，对于笛卡尔积中的每个元素，加上根节点之后形成完整的二叉搜索树，如下图所示：

举例而言，创建以 3 为根、长度为 7 的不同二叉搜索树，整个序列是 [1,2,3,4,5,6,7]，我们需要从左子序列 [1,2] 构建左子树，从右子序列 [4,5,6,7]构建右子树，然后将它们组合（即笛卡尔积）。

对于这个例子，不同二叉搜索树的个数为 F(3,7)。我们将 [1,2] 构建不同左子树的数量表示为 G(2), 从 [4,5,6,7]构建不同右子树的数量表示为 G(4)，注意到 G(n) 和序列的内容无关，只和序列的长度有关。于是，F(3,7)=G(2)⋅G(4)。 因此，我们可以得到以下公式：

F(i,n)=G(i−1)⋅G(n−i)

将公式 (1)，(2) 结合，可以得到 G(n)的递归表达式：

G(n)=∑i=1 - n G(i−1)⋅G(n−i)

至此，我们从小到大计算 G 函数即可，因为 G(n) 的值依赖于 G(0)⋯G(n−1)。

package pid096;

import java.util.Arrays;

class Solution {
    public int numTrees(int n) {
    	if(n == 1 || n == 0){
    		return 1;
    	}
    	if(n == 2){
    		return 2;
    	}
    	
    	// 0个节点 nums[0] =1
    	// 1个节点 nums[1] =1
    	// 2个节点 nums[2] =2
    	// 以上为基础
    	// 3个节点 nums[3] =(012,111,210)= nums[0]*nums[2]+nums[1]*nums[1]+nums[2]*nums[0]=2+1+2=5
    	// 就是分别计算root节点左右两侧的数量，然后计算dp[left]*dp[right]，然后遍历left与right
    	int[] nums = new int[n+1];
    	nums[0] =1;
    	nums[1] =1;
    	nums[2] =2;
    	for(int i=3;i<=n;i++){
    		int sum = 0;
    		int left = 0;
    		int right = i-1;
    		while(left<=i-1){
    			sum = sum + nums[left] * nums[right];
    			left++;
    			right--;
    		}
    		nums[i] = sum;
    	}
    	return nums[n];
    }
}