LeetCode 第 32 场双周赛(983/2957,前33.2%)
文章目录
- 1. 比赛结果
- 2. 题目
- 1. LeetCode 5468. 第 k 个缺失的正整数 easy
- 2. LeetCode 5469. K 次操作转变字符串 medium
- 3. LeetCode 5470. 平衡括号字符串的最少插入次数 medium
- 4. LeetCode 5485. 找出最长的超赞子字符串 hard
1. 比赛结果
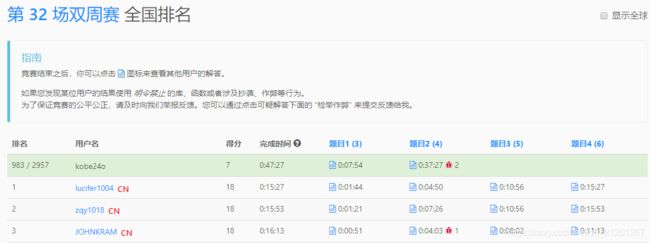
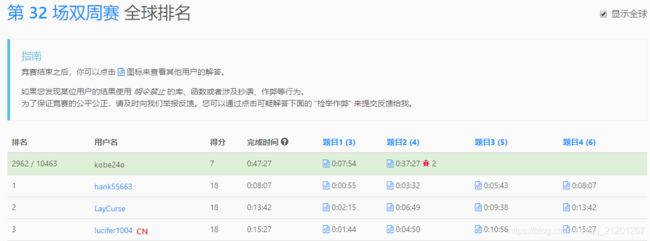
两题选手报道,继续加油!
全国排名: 983 / 2957,33.2%;全球排名: 2962 / 10463,28.3%
2. 题目
1. LeetCode 5468. 第 k 个缺失的正整数 easy
题目链接
给你一个 严格升序排列 的正整数数组 arr 和一个整数 k 。
请你找到这个数组里第 k 个缺失的正整数。
示例 1:
输入:arr = [2,3,4,7,11], k = 5
输出:9
解释:缺失的正整数包括 [1,5,6,8,9,10,12,13,...] 。
第 5 个缺失的正整数为 9 。
示例 2:
输入:arr = [1,2,3,4], k = 2
输出:6
解释:缺失的正整数包括 [5,6,7,...] 。
第 2 个缺失的正整数为 6 。
提示:
1 <= arr.length <= 1000
1 <= arr[i] <= 1000
1 <= k <= 1000
对于所有 1 <= i < j <= arr.length 的 i 和 j 满足 arr[i] < arr[j]
解题:
class Solution {
public:
int findKthPositive(vector<int>& arr, int k) {
int num = 1, ans = 1, idx = 0;
while(idx < arr.size())
{
if(arr[idx] != num)
{ //不等的时候
k--;
ans = num;
}
else
idx++;//相等时,跳过该数
if(k == 0)
break;
num++;
}
return k!=0 ? arr[arr.size()-1]+k : ans;
}
};
2. LeetCode 5469. K 次操作转变字符串 medium
题目链接
给你两个字符串 s 和 t ,你的目标是在 k 次操作以内把字符串 s 转变成 t 。
在第 i 次操作时(1 <= i <= k),你可以选择进行如下操作:
- 选择字符串 s 中满足 1 <= j <= s.length 且之前未被选过的任意下标 j (下标从 1 开始),并将此位置的字符切换 i 次。
不进行任何操作。 - 切换 1 次字符的意思是用字母表中该字母的下一个字母替换它(字母表环状接起来,所以 ‘z’ 切换后会变成 ‘a’)。
请记住任意一个下标 j 最多只能被操作 1 次。
如果在不超过 k 次操作内可以把字符串 s 转变成 t ,那么请你返回 true ,否则请你返回 false 。
示例 1:
输入:s = "input", t = "ouput", k = 9
输出:true
解释:第 6 次操作时,我们将 'i' 切换 6 次得到 'o' 。
第 7 次操作时,我们将 'n' 切换 7 次得到 'u' 。
示例 2:
输入:s = "abc", t = "bcd", k = 10
输出:false
解释:我们需要将每个字符切换 1 次才能得到 t 。
我们可以在第 1 次操作时将 'a' 切换成 'b' ,
但另外 2 个字母在剩余操作中无法再转变为 t 中对应字母。
示例 3:
输入:s = "aab", t = "bbb", k = 27
输出:true
解释:第 1 次操作时,我们将第一个 'a' 切换 1 次得到 'b' 。
在第 27 次操作时,我们将第二个字母 'a' 切换 27 次得到 'b' 。
提示:
1 <= s.length, t.length <= 10^5
0 <= k <= 10^9
s 和 t 只包含小写英文字母。
解题:
- 每个字符找对应的字符,如果两对字符都是相差5,那么第二对就要多转一圈,5+26
class Solution {
public:
bool canConvertString(string s, string t, int k) {
if(s.size() != t.size())
return false;
int diff;
vector<int> count(26, 0);
for(int i = 0; i < s.size(); ++i)
{
if(s[i] == t[i])
continue;
if(s[i] < t[i])
diff = t[i]-s[i];
else if(s[i] > t[i])
diff = 'z'-s[i]+t[i]-'a'+1;
count[diff]++;//diif次转换,有多少次
}
for(int i = 0; i < 26; ++i)
{
if((count[i]-1)*26+i > k)//需要的转换次数最大值,超了
return false;
}
return true;
}
};
3. LeetCode 5470. 平衡括号字符串的最少插入次数 medium
题目链接
给你一个括号字符串 s ,它只包含字符 '(' 和 ')' 。一个括号字符串被称为平衡的当它满足:
- 任何左括号
'('必须对应两个连续的右括号'))'。 - 左括号
'('必须在对应的连续两个右括号'))'之前。
比方说 "())", "())(())))" 和 "(())())))" 都是平衡的, ")()", "()))" 和 "(()))" 都是不平衡的。
你可以在任意位置插入字符 '(' 和 ')' 使字符串平衡。
请你返回让 s 平衡的最少插入次数。
示例 1:
输入:s = "(()))"
输出:1
解释:第二个左括号有与之匹配的两个右括号,
但是第一个左括号只有一个右括号。
我们需要在字符串结尾额外增加一个 ')'
使字符串变成平衡字符串 "(())))" 。
示例 2:
输入:s = "())"
输出:0
解释:字符串已经平衡了。
示例 3:
输入:s = "))())("
输出:3
解释:添加 '(' 去匹配最开头的 '))' ,
然后添加 '))' 去匹配最后一个 '(' 。
示例 4:
输入:s = "(((((("
输出:12
解释:添加 12 个 ')' 得到平衡字符串。
示例 5:
输入:s = ")))))))"
输出:5
解释:在字符串开头添加 4 个 '('
并在结尾添加 1 个 ')' ,
字符串变成平衡字符串 "(((())))))))" 。
提示:
1 <= s.length <= 10^5
s 只包含 '(' 和 ')' 。
解题:
类似题目:LeetCode 921. 使括号有效的最少添加(栈)
class Solution {
public:
int minInsertions(string s) {
int sum = 0;
stack<char> stk;
int n = s.size();
for(int i = 0; i < n; ++i)
{
if(s[i] == '(')
stk.push('(');
else if(s[i] == ')')
{
if(i+1 < n && s[i+1] == ')')
{
if(!stk.empty())
stk.pop();// ())消除
else
sum++;//补一个左括号
i++;//后面的 ) 已经处理了
}
else//后面没有 )
{
if(!stk.empty())
{ //有左括号
stk.pop();
sum++;// 补一个右括号
}
else//没有左括号
sum += 2;//补一个左,一个右括号
}
}
}
while(!stk.empty())
{
stk.pop();
sum += 2;
}
return sum;
}
};
借助921题思路
class Solution {
public:
int minInsertions(string s) {
//先预处理,把 )) 变成 )
string ans;
int l = 0, r = 0, sum = 0;
for(int i = 0; i < s.size(); ++i)
{
if(i+1 < s.size() && s[i]==')' && s[i+1] == ')')
{
ans += ")";//连续的两个变成1个 )
i++;
continue;
}
if(s[i] == ')')
sum++;//落单的 )记录下来有多少个
ans += s[i];
}
for(int i = 0; i < ans.size(); ++i)
{ //921 题的套路
if(ans[i] == '(')
l++;
else
{
if(l>0) //右括号可以与之匹配
l--;
else //右括号没有相应的左括号匹配
r++;
}
}
return 2*l+r+sum;
}
};
4. LeetCode 5485. 找出最长的超赞子字符串 hard
题目链接
给你一个字符串 s 。请返回 s 中最长的 超赞子字符串 的长度。
「超赞子字符串」需满足满足下述两个条件:
- 该字符串是 s 的一个非空子字符串
- 进行任意次数的字符交换重新排序后,该字符串可以变成一个回文字符串
示例 1:
输入:s = "3242415"
输出:5
解释:"24241" 是最长的超赞子字符串,
交换其中的字符后,可以得到回文 "24142"
示例 2:
输入:s = "12345678"
输出:1
示例 3:
输入:s = "213123"
输出:6
解释:"213123" 是最长的超赞子字符串,
交换其中的字符后,可以得到回文 "231132"
示例 4:
输入:s = "00"
输出:2
提示:
1 <= s.length <= 10^5
s 仅由数字组成
解题:
- 状态压缩+哈希记录第一次出现的状态
class Solution {
public:
int longestAwesome(string s) {
if(s.size() <= 1) return s.size();
unordered_map<int, int> m;
m[0] = -1;//空字符所有的0-9位都是0
int maxlen = 1, state = 0;
for(int i = 0; i < s.size(); ++i)
{
state ^= (1<<(s[i]-'0'));//该数位奇偶变化了
if(m.count(state))//相同的状态,同奇同偶,相减还是偶数个
maxlen = max(maxlen, i-m[state]);
else
m[state] = i;
//考虑有一个位不一样,就是相减后只有一个位是奇数,还是回文
for(int j = 0; j < 10; ++j)
{
int odd_state = state^(1<<j);
if(m.count(odd_state))
maxlen = max(maxlen, i-m[odd_state]);
}
}
return maxlen;
}
};
我的CSDN博客地址 https://michael.blog.csdn.net/
长按或扫码关注我的公众号(Michael阿明),一起加油、一起学习进步!
![]()