LeetCode 第 201 场周赛(304/5614,前5.42%)
文章目录
- 1. 比赛结果
- 2. 题目
- 1. LeetCode 5483. 整理字符串 easy
- 2. LeetCode 5484. 找出第 N 个二进制字符串中的第 K 位 medium
- 3. LeetCode 5471. 和为目标值的最大数目不重叠非空子数组数目 medium
- 4. LeetCode 5486. 切棍子的最小成本 hard
1. 比赛结果
做出来3题,第二题暴力可以过,我想着不行,找规律失败。继续加油!
全国排名: 304 / 5614,5.42%;全球排名: 956 / 15616,6.12%

2. 题目
1. LeetCode 5483. 整理字符串 easy
题目链接
给你一个由大小写英文字母组成的字符串 s 。
一个整理好的字符串中,两个相邻字符 s[i] 和 s[i + 1] 不会同时满足下述条件:
- 0 <= i <= s.length - 2
- s[i] 是小写字符,但 s[i + 1] 是相同的大写字符;反之亦然 。
请你将字符串整理好,每次你都可以从字符串中选出满足上述条件的 两个相邻 字符并删除,直到字符串整理好为止。
请返回整理好的 字符串 。题目保证在给出的约束条件下,测试样例对应的答案是唯一的。
注意:空字符串也属于整理好的字符串,尽管其中没有任何字符。
示例 1:
输入:s = "leEeetcode"
输出:"leetcode"
解释:无论你第一次选的是 i = 1 还是 i = 2,
都会使 "leEeetcode" 缩减为 "leetcode" 。
示例 2:
输入:s = "abBAcC"
输出:""
解释:存在多种不同情况,但所有的情况都会导致相同的结果。例如:
"abBAcC" --> "aAcC" --> "cC" --> ""
"abBAcC" --> "abBA" --> "aA" --> ""
示例 3:
输入:s = "s"
输出:"s"
提示:
1 <= s.length <= 100
s 只包含小写和大写英文字母
解题:
- 使用栈解题
class Solution {
public:
string makeGood(string s) {
if(s.size() <= 1)
return s;
string ans;
stack<char> stk;
for(int i = 0; i < s.size(); ++i)
{
if(!stk.empty() && ((s[i]-stk.top()==32)
|| (stk.top()-s[i]==32)))
stk.pop();//前后是大小写关系
else
stk.push(s[i]);
}
while(!stk.empty())
{
ans = stk.top()+ans;
stk.pop();
}
return ans;
}
};
2. LeetCode 5484. 找出第 N 个二进制字符串中的第 K 位 medium
题目链接
给你两个正整数 n 和 k,二进制字符串 Sn 的形成规则如下:
S1 = "0"- 当 i > 1 时,
Si = Si-1 + "1" + reverse(invert(Si-1))
其中 + 表示串联操作,reverse(x) 返回反转 x 后得到的字符串,而 invert(x) 则会翻转 x 中的每一位(0 变为 1,而 1 变为 0)
例如,符合上述描述的序列的前 4 个字符串依次是:
S1 = "0"
S2 = "011"
S3 = "0111001"
S4 = "011100110110001"
请你返回 Sn 的 第 k 位字符 ,题目数据保证 k 一定在 Sn 长度范围以内。
示例 1:
输入:n = 3, k = 1
输出:"0"
解释:S3 为 "0111001",其第 1 位为 "0" 。
示例 2:
输入:n = 4, k = 11
输出:"1"
解释:S4 为 "011100110110001",其第 11 位为 "1" 。
示例 3:
输入:n = 1, k = 1
输出:"0"
示例 4:
输入:n = 2, k = 3
输出:"1"
提示:
1 <= n <= 20
1 <= k <= 2^n - 1
解题:
- 比赛没想着暴力法,暴力很简单
class Solution {
public:
char findKthBit(int n, int k) {
if(n==1 || k==1) return '0';
string s = "0", next;
while(--n)
{
next = s+"1";
for(int i = s.size()-1; i >= 0; --i)
next += s[i]=='1' ? '0' : '1';
s = next;
}
return s[k-1];
}
};
循环解法:
class Solution {
public:
char findKthBit(int n, int k) {
if(k==1 || n==1)
return '0';
k--;
int len = (1<<n)-1;//字符串长度为2^n-1
if(k == len/2) return '1';
bool reverse = false;
while(n)
{
len = (1<<n)-1;//字符串长度为2^n-1
if(k == 0)//找到最前面了,状态不会再变
break;
else if(k > len/2)
{
reverse = !reverse;//后半部分会反转状态
k = len-1-k;//位置对应于前一个字符的位置
}
n--;
}
return reverse ? '1' : '0';
}
};
递归解法
class Solution {
public:
char findKthBit(int n, int k) {
if(k==1 || n==1)
return '0';
k--;
int len = (1<<n)-1;//字符串长度为2^n-1
if(k == len/2) return '1';
return dfs(n, k);
}
char dfs(int n, int k)
{
if(n==1 || k == 0)
return '0';
int len = (1<<n)-1;
if(k == len/2)
return '1';
if(k > len/2)
return dfs(n-1, len-1-k)=='1' ? '0' : '1';
return dfs(n-1, k);
}
};
3. LeetCode 5471. 和为目标值的最大数目不重叠非空子数组数目 medium
题目链接
给你一个数组 nums 和一个整数 target 。
请你返回 非空不重叠 子数组的最大数目,且每个子数组中数字和都为 target 。
示例 1:
输入:nums = [1,1,1,1,1], target = 2
输出:2
解释:总共有 2 个不重叠子数组(加粗数字表示) [1,1,1,1,1] ,
它们的和为目标值 2 。
示例 2:
输入:nums = [-1,3,5,1,4,2,-9], target = 6
输出:2
解释:总共有 3 个子数组和为 6 。
([5,1], [4,2], [3,5,1,4,2,-9]) 但只有前 2 个是不重叠的。
示例 3:
输入:nums = [-2,6,6,3,5,4,1,2,8], target = 10
输出:3
示例 4:
输入:nums = [0,0,0], target = 0
输出:3
提示:
1 <= nums.length <= 10^5
-10^4 <= nums[i] <= 10^4
0 <= target <= 10^6
解题:
- 使用哈希记录状态,贪心,找到一个存在状态,子数组+1,哈希清空(题目要求无重复的子数组)
class Solution {
public:
int maxNonOverlapping(vector<int>& nums, int target) {
unordered_set<int> set;
set.insert(0);//和为0存在
int sum = 0, count = 0;
for(int i = 0; i < nums.size(); ++i)
{
sum += nums[i];
if(set.count(sum-target))
{
count++;
set.clear();
}
set.insert(sum);
}
return count;
}
};
4. LeetCode 5486. 切棍子的最小成本 hard
题目链接
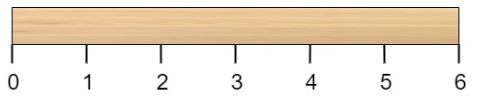
有一根长度为 n 个单位的木棍,棍上从 0 到 n 标记了若干位置。例如,长度为 6 的棍子可以标记如下:
给你一个整数数组 cuts ,其中 cuts[i] 表示你需要将棍子切开的位置。
你可以按顺序完成切割,也可以根据需要更改切割的顺序。
每次切割的成本都是当前要切割的棍子的长度,切棍子的总成本是历次切割成本的总和。
对棍子进行切割将会把一根木棍分成两根较小的木棍(这两根木棍的长度和就是切割前木棍的长度)。请参阅第一个示例以获得更直观的解释。
返回切棍子的 最小总成本 。
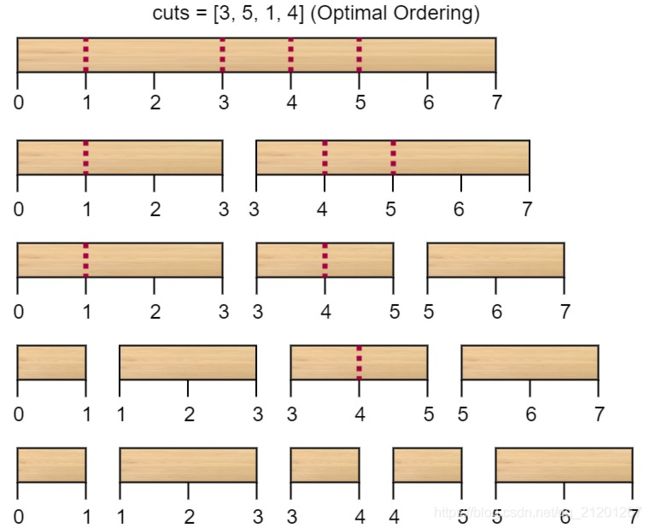
输入:n = 7, cuts = [1,3,4,5]
输出:16
解释:按 [1, 3, 4, 5] 的顺序切割的情况如下所示:
第一次切割长度为 7 的棍子,成本为 7 。
第二次切割长度为 6 的棍子(即第一次切割得到的第二根棍子),
第三次切割为长度 4 的棍子,最后切割长度为 3 的棍子。
总成本为 7 + 6 + 4 + 3 = 20 。
而将切割顺序重新排列为 [3, 5, 1, 4] 后,总成本 = 16
(如示例图中 7 + 4 + 3 + 2 = 16)。
示例 2:
输入:n = 9, cuts = [5,6,1,4,2]
输出:22
解释:如果按给定的顺序切割,则总成本为 25 。
总成本 <= 25 的切割顺序很多,
例如,[4,6,5,2,1] 的总成本 = 22,
是所有可能方案中成本最小的。
提示:
2 <= n <= 10^6
1 <= cuts.length <= min(n - 1, 100)
1 <= cuts[i] <= n - 1
cuts 数组中的所有整数都 互不相同
解题:
- 区间DP
class Solution {
int ans = 0;
public:
int minCost(int n, vector<int>& cuts) {
if(cuts.size() == 1) return n;
cuts.push_back(0);
cuts.push_back(n);
sort(cuts.begin(), cuts.end());
int m = cuts.size(), i, j;
vector<vector<int>> dp(m, vector<int>(m, 0x7f7f7f7f));
for(int i = 1; i < m; ++i)
dp[i-1][i] = 0;//最小的段不需要切成本为0,最小区间
for(int len = 2; len < m; ++len)//区间变大
{
for(int i = 0; i < m; ++i)//枚举左端点
{
int j = i+len;//右端点
if(j >= m) continue;
for(int k = j-1; k > i; --k)//从左右端点中间枚举切分点
{
dp[i][j] = min(dp[i][j], dp[i][k]+dp[k][j]+cuts[j]-cuts[i]);
//左右两段的成本+切开本次的成本cuts[j]-cuts[i](总长度)
}
}
}
return dp[0][m-1];
}
};
我的CSDN博客地址 https://michael.blog.csdn.net/
长按或扫码关注我的公众号(Michael阿明),一起加油、一起学习进步!
![]()