机试备考——刷题攻略
为了准备保研的机试,在学习完常见算法后,开始了刷题!看了一些大佬的心得分享,总结了一下。
题目类型分为:
数组、字符串、高精度计算、排序、递推、递归、搜索与回溯、贪心算法、分治算法、动态规划、栈、队列、树、图论算法
按类型刷,刷完后做笔记。
因为不喜欢LeetCode那种答案要封装起来的写法,我选择了在N诺/洛谷上刷题。
接下来我总结了一下我刷题的重点题目和答案。
刷题目录
- N诺
- 简单模拟(答案链接)
- 01序列
- 随机数
- 日期
- 单链表
- 链表合并
- 删除字符串
- 阶乘求和
- 括号的匹配
- 基础算法
- 成绩排序
- 玛雅人的秘密
- 最简真分数
- 逆序对
- 搜索
- 奇怪的电梯
- 生化武器
- 洛谷
- 搜索
- P2392 kkksc03考前临时抱佛脚
- P1443 马的遍历
- P2895 [USACO08FEB]Meteor Shower S
- P2036 [COCI2008-2009#2] PERKET
- P1433 吃奶酪
- P1019 单词接龙
- P1101 单词方阵
- P1032 字串变换
- P1162 填涂颜色
- 贪心
- P2240 部分背包问题
- P1803 区间贪心
- P1090 合并果子
- P1106 删数问题
- 线性表
- P3613 【深基15.例2】寄包柜
- P4387 【深基15.习9】验证栈序列
- P2234 [HNOI2002]营业额统计
- 二叉树
- P4913 【深基16.例3】二叉树深度
- P1229 遍历问题
- 图
- P5318 查找文献
- P3916 图的遍历
- P1807 最长路
- P1127 词链
- P1363幻向迷宫
- P1347 排序
- 最短路
- P1119 灾后重建
- P3371 单源最短路径
- 最小生成树
- P3366最小生成树
- P2872 修路
- 动态规划(基本+线性状态)
- P1434 滑雪
- P 1002 过河卒
- 导弹拦截
- P4933 大师
- P1233 木棍加工
- 动态规划(区间和环形、树或图)
- P1880 石子合并
N诺
分类和提交的感觉都挺好的,就是题目太少了,所以后来主刷洛谷
简单模拟(答案链接)
01序列
对于长度为6位的一个01串,每一位都可能是0或1,一共有64种可能。它的前几个是:
000000
000001
000010
000011
000100
请按从小到大的顺序输出这64种01串。
思路: 将0~63分别进行十进制转二进制,然后用“%06d”格式输出。(进制转换)
随机数
从1—20之间随机抽取5个数,输出抽取出来的5个数之和与剩余未被抽取的15个数之和的总和。
思路:题目很蠢,就是1+····+20求和,只是之前没有遇到过随机数,所以记录一下。
产生一定范围随机数的通用表示公式:
- 要取得[a,b)的随机整数,使用(rand() % (b-a))+ a;
- 要取得[a,b]的随机整数,使用(rand() %(b-a+1))+ a;
- 要取得(a,b]的随机整数,使用(rand() % (b-a))+ a + 1; 通用公式:a +rand() % n;其中的a是起始值,n是整数的范围。
- 要取得a到b之间的随机整数,另一种表示:a + (int)b * rand()/ (RAND_MAX + 1)。
- 要取得0~1之间的浮点数,可以使用rand() / double(RAND_MAX)。
a[i] = rand()%(20-1+1) + 1;//产生1-20之间的随机数
日期
今天是2012年4月12日星期四,编写程序,输入今天(2012年)开始到12月31日之间的任意日期,输出那一天是星期几。例如输入“5(回车)20(回车)”(5月20日),输出应为“Sunday”。
更多有关日期的问题见。
计算输入日期和20120412之间的天数
之后天数+4(星期四)
对7取模得到的余数就是星期几
单链表
设节点定义如下
struct Node {
int Element; // 节点中的元素为整数类型
struct Node * Next; // 指向下一个节点
};
从键盘输入5个整数,将这些整数插入到一个链表中,并按从小到大次序排列,最后输出这些整数。
练习单链表的建立和排序!
链表合并
给定两个元素有序(从小到大)的链表,要求将两个链表合并成一个有序(从小到大)链表。
思路:类似合并排序,只不过将数组变为链表的形式。
while(p1 && p2) //判断两个链表是否有一个合并结束
删除字符串
给你一个字符串S,要求你将字符串中出现的所有"gzu"(不区分大小写)子串删除,输出删除之后的S。
就是说出现“Gzu”、“GZU”、“GZu”、"gzU"都可以删除。
思路:STL的string容器中提供transform函数(大小写转换)、find函数(找到子串位置)和erase函数(删除部分区间子串)。
阶乘求和
求Sn=1!+2!+3!+4!+5!+…+n!之值,其中n是一个数字。
思路:直接使用递归会导致超时。使用
for (int i = 1; i <= n; i++) {
num *= i;
ans += num;
}
来降低复杂度
括号的匹配
在算术表达式中,除了加、减、乘、除等运算外,往往还有括号。包括有大括号{},中括号[],小括号(),尖括号<>等。 对于每一对括号,必须先左边括号,然后右边括号;如果有多个括号,则每种类型的左括号和右括号的个数必须相等;对于多重括号的情形,按运算规则,从外到内的括号嵌套顺序为:大括号->中括号->小括号->尖括号。例如,{[()]},{()},{{}}为一个合法的表达式,而([{}]),{([])},[{<>}]都是非法的。
注意:同级嵌套是允许的(如:{{}}),使用栈来答题
遍历字符串,遇到左括号时,先和栈顶元素判断是否符合括号优先级,不符合直接GG。否则入栈。
遇到右括号时,看和栈顶的括号是否相匹配,是的话弹出栈顶元素,不是的话直接GG。
最后再判断一下栈内元素是否全部弹出,栈内还有括号未匹配,直接GG,否则合法。
栈在使用pop()时需要先判断empty()
注意:使用goto来跳出多重循环,此时continue只能跳出一层
基础算法
成绩排序
题目:输入任意(用户,成绩)序列,可以获得成绩从高到低或从低到高的排列,相同成绩都按先录入排列在前的规则处理。
当遇到相同数据按输入顺序排列的时候要使用稳定排序stable_sort()【不能使用sort()】
玛雅人的秘密
玛雅人有一种密码,如果字符串中出现连续的2012四个数字就能解开密码。给一个长度为N的字符串,(2= 参考https://www.jianshu.com/p/fa96e0c90e0e的思路。 给出n个正整数,任取两个数分别作为分子和分母组成最简真分数,编程求共有几个这样的组合。 思路: 猫猫 TOM 和小老鼠 JERRY 最近又较量上了,但是毕竟都是成年人,他们已经不喜欢再玩那种你追我赶的游戏,现在他们喜欢玩统计。 放在合并排序代码中间计算逆序对个数 呵呵,有一天我做了一个梦,梦见了一种很奇怪的电梯。大楼的每一层楼都可以停电梯,而且第i层楼(1<=i<=N)上有一个数字Ki (0<=Ki<=N)。电梯只有四个按钮:开,关,上,下。上下的层数等于当前楼层上的那个数字。当然,如果不能满足要求,相应的按钮就会失灵。例如:3 3 1 2 5代表了Ki(K1=3,K2=3,……),从一楼开始。在一楼,按“上”可以到4楼,按“下”是不起作用的,因为没有-2楼。那么,从A楼到B楼至少要按几次按钮呢? 使用BFS进行搜索,每次在岔路口选择+ki或者-ki,如果在第x步得到了B,那么直接返回x。 在一个封闭的房间里,gogo给大家表演了他的屁遁术,人果然一下没影了,但是他留下的“生化武器”,却以每秒1米的速度向上下左右扩散出去。为了知道自己会不会被“毒”到,你果断写了个算法计算出了“毒气”在t秒时间内可以到达的所有地方。 样例输入: 当遇到每行输入的字符个数不一定时,不能使用双层循环输入二维数组G,而是使用单层循环,直接用cin>>G[i],来输入一整行。 题目:https://www.luogu.com.cn/problem/P2392 使用DFS。 https://www.luogu.com.cn/problem/P1443 依旧是像走迷宫问题一样,向dis[8][2]的八个方向走下一步,依次入队。使用BFS。 https://www.luogu.com.cn/problem/P2895 看了大佬的答题思路,发现了题目的隐藏坑点! 之后利用BFS,直到某一点不会被陨石覆盖(将陨石覆盖的点声明一个二维数组来记录图中所有点的砸落时间,若为-1初始值,则是安全位置),则输出。 题目:https://www.luogu.com.cn/problem/P2036 dfs()中依次遍历每一种配料,每种配料可选择添加或者不添加两种分支。直到遍历完所有配料返回 题目:https://www.luogu.com.cn/problem/P1433 状压入门!参考https://www.cnblogs.com/iss-ue/p/12458651.html (1<<(i-1))表示第i位是1,其他都是0的二进制 题目:https://www.luogu.com.cn/problem/P1019 依旧是DFS遍历整个字符串数组找到下一个接龙字符串。 如何判断接龙及接龙长度: for循环遍历重叠字符串长度,再次for循环判断两个字符串收尾相应位置是否相同,若均相同则返回当前长度为重叠字符串长度。若长度为0,则表示不可以接龙。 则当前连接串长度为nowlength+str[i].length()-重叠长度 每次dfs都更新最长长度。 题目:https://www.luogu.com.cn/problem/P1101 依旧使用dfs,index+1直到遍历出整个“yizhong”字符串(index==7)为止。 如何选取初始点: 先在图中进行遍历找到相邻同方向的‘y’和‘i’,然后代入dfs ‘y’的位置和已经确定的方向k来找到满足完整“yizhong”字符串的位置,并记录下来。 使用一个point结构体数组来储存7个字符的位置,使用vis数组来表示需要显示原字符的位置。 注意string的一些常用函数 如果是string查重的话: 使用DFS,每次递归向四个方向dfs,如果遇到边界或者地图上值为1(墙)就返回,符合条件则染色。这样递归下来被染色的都是墙之外的。只要判断哪些被染色了,就按原样输出,其他的墙内元素进行染色。 题目:https://www.luogu.com.cn/problem/P2240 注意这类问题的通式: 先声明一个结构体来存重量,价值和单位价值。 读入数据后,计算每类物品的单位价值,然后按单位价值从高到低排序 之后循环所有物品,每次选择单价最高的物品,如果重量<=背包:将该物品所有全部装入;如果重量>背包,将单价*背包容量的装入。 问题:https://www.luogu.com.cn/problem/P1803 比较左端点坐标不同,则大的在前;相同,则按右端点小的在前 问题:https://www.luogu.com.cn/problem/P1090 使用优先队列存放哈夫曼树的结点。因为优先队列可以保持时刻队列中都是有序的。 问题:https://www.luogu.com.cn/problem/P1106 写出删去数字的过程,然后找到规律,进行编程模拟 如果遇到逆序的两个元素,就删去第一个。一直循环删去的数字的次数。 题目:https://www.luogu.com.cn/problem/P3613 如果直接用二维数组表示柜子和格子,会超时 因此使用map,map的时间复杂度是会log的,而且只需要建立值的107级的映射。 二维map: 只需要保证每次入栈后都进行判断,是否当前栈顶元素和出栈序列首元素相同,相同就出栈,同时序列前进1,直到所有元素都入栈过,过此时栈空,则说明序列是出栈序列。 距离当前数最近的只有将之前的序列排序后,该数插入位置的前后位置上的数。 使用set可以直接自动排序并去重,使用s.lower_bound(x)返回大于等于x的位置迭代器(iterator)。【使用二分查找找到x应该插入的位置】 二叉树可以用数组静态表示 找二叉树的最大深度,就是遍历根节点到叶节点的每一条路径,不断更新最大深度。(DFS) 已知前序和后序遍历序列,求中序遍历序列的个数。 只知道前序和后序序列,中序序列的不确定性在于不知道子节点是左子树还是右子树。 根节点为a,根节点的左子树一定是以b为根节点,此时若b恰好为后序序列的a之前一位,那么说明根节点a没有第二棵子树,此时子树bc可以为左子树也可以为右子树,因此有两种情况。 此时,则bc分别为a的左右子树,中序序列固定,只有一种情况。 因此使用DFS对一棵树进行深搜,左子树的情况*右子树的情况 * 总根节点a的情况即为总的中序序列个数。 递归边界为:此时树只有一个结点或无节点,则只有一种情况。 计算左子树的长度,需要一个index数组记录下来后序序列中每个字符的位置。 此时左子树的根节点在后序序列中的位置-后序序列开头index+1,即为左子树的结点个数。 如果先序序列根节点index+左子树结点个数== 先序序列的最后一个节点index,则根节点只有一个子树,此时子树情况有两种,可以为左或右。 之后再对先序序列根节点的左子树和右子树分别进行dfs,得到每一层的情况数,再相乘即为最后的结果。 该题中顶点个数为105,注意,此时如果使用邻接矩阵存图会导致运行超时。因此要使用邻接表存图。 因为题目中提到了如果有很多篇文章可以参阅,请先看编号较小的那篇,因此等输入邻接表结束后,需要对每个顶点的adj[i]进行sort排序 其余是基本的图的DFS和BFS遍历方法,见文章 图算法专题(一)【定义、存储和遍历】 如果仍超时的话,可以使用adj邻接表存储边(关系),使用edge结构体表示x->y。这样排序对整个邻接表cmp,如果x相同,y小的在前面,如果不相同,x小的在前面。 寻找每个结点DFS路径上的最大结点编号。 求DAG图的最长路。 把所有单词当做结点,如果两个单词之间可以接龙,那么说明这两个结点间有一条边,这样就把问题转换成了图的DFS问题。 典型的dfs题,但是要注意没有指明出口的位置,而是“如果它们能走到距离起点无限远处,就认为能走出去”。 使用一个三维数组来分别存储第一维代表访问过,第二维代表取模后的x坐标,第三维代表取模后的y坐标,这样来节省空间。 考察拓扑排序。 题目:https://www.luogu.com.cn/problem/P1119 利用Floyd算法,每次更新所有点之间的最短距离。 使用G[maxn][maxn]邻接矩阵存储图,初始化图中所有点之间距离为INF。注意的点是题中给了一个时间条件,当进行floyd的时候使用中转的k点是有限制的,必须time[k]小于当前问题给出的时间,此时才可以用k来更新所有点的最短距离。 因此使用floyd的时候最外层的k已经固定,只需要两层循环i和j即可,依旧是 在输出时也要注意当前求得两个城市的time是否≤当前时间,只有≤才可以输出。 题目中可能有负权,因此使用SPFA 注意最小生成树是无向图,用邻接表存的话 使用prim算法,用结构体储存边,对边进行排序后,从小到大进行查并集如果不在一个连通块就合并。 记忆化搜索,用来减少搜索次数,防止超时 用s数组存放记忆 滑雪向四周dfs遇到小于自己数的就进行dfs 由于卒只能往下方或右方走 一个系统能拦截多少导弹,即求序列的不上升子序列最大长度。 题目:https://www.luogu.com.cn/problem/P4933 状态转移方程: +20000是为了保证差值不为负数;+1是以i和j两个电塔组成的方案 在每次内层循环后都使用: 最后 问题:https://www.luogu.com.cn/problem/P1233 此问题类似于导弹拦截问题,但是是二维的,因此,我们先按第一维从大到小排序,这样在前面的先加工后面的一定可以不花费时间加工。 区间dp,如果求最大值,那么要保证每个区间都是区间当前能达到的最大值。 如何解决环形问题: 因此需要枚举一个k,来作为这一圈石子的分割线。 状态转移方程: 此时j的大小因为是环形不方便循环枚举,因此我们使用len来枚举区间长度(2~n),这样j=i+len-1
使用bfs层次遍历树
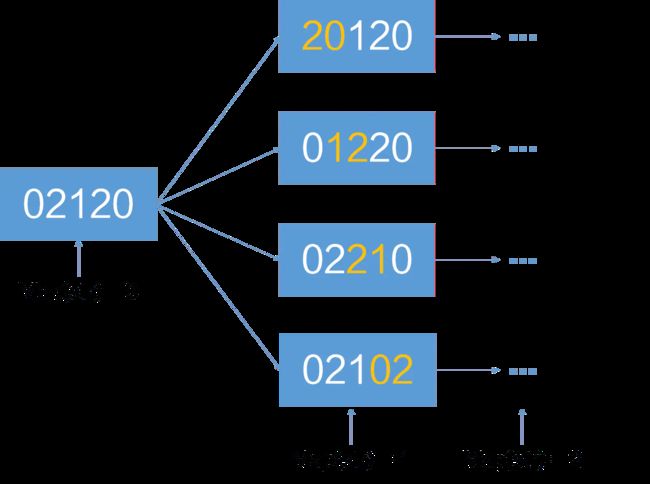
最简真分数
最简真分数 = 分子和分母的最大公因数为1逆序对
最近,TOM 老猫查阅到一个人类称之为“逆序对”的东西,这东西是这样定义的:对于给定的一段正整数序列,逆序对就是序列中 ai>aj 且 i
第一行,一个数 n,表示序列中有 n个数(n < 10^5)。
第二行 n 个数,表示给定的序列。序列中每个数字不超过 10^9。
当输入数字很大的时候,直接使用两层循环会导致超时,只能过一半的数据。
使用分治+归并排序。
读入的数每次划分后合并时左右子区间都是从小到大排好序的,我们只需要统计左边区间每一个数分别会与右边区间产生多少逆序对即可。
(因为在左边的数无论怎么排序,排序好后还是都是在 右边的数的前面。所以我们可以查下左边与右边能产生多少对逆序对就好了。
又因为左边的是按小到大排序的
所以只要左边第一个 > 右边第一个,那么表示左边所有数都大于右边第一个,左边多少数就有多少对逆序。然后让右边的指向第二个。继续重复(ans += mid -i +1;)
如果左边第一个小于右边第一个,那就让左边指向第二个,然后继续。while(i<=R1 && j<=R2){
if(a[i]<=a[j]){
b[index++] = a[i++];
}else{
b[index++] = a[j++];
ans += R1-i+1;//统计逆序对数
}
}
搜索
奇怪的电梯
输入文件共有二行,第一行为三个用空格隔开的正整数,表示N,A,B(1≤N≤200, 1≤A,B≤N),第二行为N个用空格隔开的正整数,表示Ki。
输出按钮次数。生化武器
输入输出格式
输入描述:
有多组测试数据
第一行输入n,m,t(0
输出描述:
如果在t秒时间内毒气没有充满房间或刚好充满,输出现在房间里的情况,‘#’表示有‘毒气’的地方
否则,输出“No”
每组数据输出后有一个空行
9 9 4
XXXXXXXXX
X…X…X
X.*…X
X…X…X
XXXXXXXXX
X…X
X…X
X…X
XXXXX
依旧使用BFS进行搜索,每次向上下左右移动一步,同时保持时间洛谷
搜索
P2392 kkksc03考前临时抱佛脚
每道题可以选择放在左脑解决或者是右脑解决,因此遍历每道题放在哪个脑子,然后求两边最大值的最小值,就是答案。P1443 马的遍历
注意左对齐,宽5格,不能到达则输出-1 输出格式
"%-5d" -表示左对齐
注意象棋中马走日,因此是八个方向P2895 [USACO08FEB]Meteor Shower S
P2036 [COCI2008-2009#2] PERKET
void dfs(int index,int sums,int sumt){//sums酸度,sumt甜度
if(index >n){
if(sums==1&&sumt==0) return;//清水
minabs = min(minabs,abs(sums-sumt));
return;
}
//分两种情况,一种是添加 2.不添加
dfs(index+1,sums*s[index],sumt+t[index]);
dfs(index+1,sums,sumt);
}
P1433 吃奶酪
P1019 单词接龙
P1101 单词方阵
P1032 字串变换
str.find(substr)!=string::npos此时可以在str中找到substr子串,str.find()返回子串第一次出现的位置index
str.replace(pos,len,str2)把str从pos号位开始,长度为len的子串替换为str2.
使用set< string > vis;如果vis.count(str) == 0 则说明没有出现过str子串,否则就是重复的,之后再把str放入set:vis.insert(str)P1162 填涂颜色
贪心
P2240 部分背包问题
P1803 区间贪心
注意排序区间cmp的规则:bool cmp(contest x, contest y){
if(x.a != y.a) return x.a>y.a;
else return x.b < y.b;//左端点相同按右端点从小到大排序
}
P1090 合并果子
//设置优先级队列,值越小优先级越高
priority_queue<int,vector<int>,greater<int> > q;//存放果子
P1106 删数问题
线性表
P3613 【深基15.例2】寄包柜
map
对应m[str1][str2] = int;P4387 【深基15.习9】验证栈序列
P2234 [HNOI2002]营业额统计
二叉树
P4913 【深基16.例3】二叉树深度
struct node{
int left,right;
}tree[maxn];
P1229 遍历问题
a b c
c b a
a b c
b c a
int ltree = index[s1[st1+1]]-st2+1;
for(int i =0;i<len;i++){
index[s2[i]] = i;//记录s2中每个字符的位置
}
if(st1+ltree == en1) k=2;
图
P5318 查找文献
for(int i=1;i<=n;i++){
sort(adj[i].begin(),adj[i].end());
}
P3916 图的遍历
可以反向建图,这样从n到1依次dfs的时候结点i所到达的所有节点的最大编号均为i。 for(int i =1;i<=m;i++){
int a,b;
scanf("%d %d",&a,&b);
adj[b].push_back(a);//反向建图
}
P1807 最长路
见动态规划专题。P1127 词链
使用双重循环遍历所有的单词for(int i=1;i<=n;i++){//找边
for(int j =1;j<=n;j++){
if(i==j) continue;//减少次数
if(s[i][len[i]-1]==s[j][0]) G[i][j]=1;
}
}
abc.cde 发现‘c’出现在首部和出现在尾部都是1次,而‘a’由于是起始单词则只有出现在首部一次。
aloha.arachnid 发现’a’出现在首部2次,出现在尾部1次
因此可以总结出规律:
起始单词的首字母出现在开头的次数 = 出现在尾部的次数+1int findS(){//找起始单词
for(int i =1;i<=n;i++){
if(st[s[i][0]]-en[s[i][0]] == 1)
return i;
}
return 1;//找不到满足规则的,就把第一个当做起始单词
}
此时在dfs函数中要加一个flag判断,如果为1时立即return,这样才放置回溯时把答案覆盖了。【只需要第一次dfs到底就可以结束】P1363幻向迷宫
此时,如果一个人走到过某个点现在又走到了这个点,那显然是可以走无限远的。
我们使用x,y和lx,ly来分别代表每次进行+dis[i](向四周走)时取模,和未取模。如果第一次走到某个点,显然x==lx, y ==ly;所以如果某个点已走过,同时它的x !=lx || y !=ly,说明第二次走到该点,则此时flag ==true,已经走出去了。
同时注意随时判断flag,进行剪枝。if(vis[x][y][0]&&(vis[x][y][1]!=lx ||vis[x][y][2]!=ly)){
flag = true;
return;
}
P1347 排序
可以将字母使用G[ch-‘A’]来转化为数字。
判断图中是否成环:
如果拓扑排序没能遍历所有的点(就是最后拓扑序列中的个数不为n),就说明存在一个环。
在子函数中使用exit(0);可以直接退出程序,等同于main函数中的return 0;最短路
P1119 灾后重建
if(G[i][j] > G[i][k]+G[k][j]) G[i][j] = G[i][k]+G[k][j];P3371 单源最短路径
注意初始化时dis数组一定要足够大(1e10)最小生成树
P3366最小生成树
Adj[x].push_back(node(y,z)); Adj[y].push_back((node(x,z)));
双向都要存P2872 修路
动态规划(基本+线性状态)
P1434 滑雪
每次搜索记录下来已经已经搜索过的点的值,下次搜到这个点,直接用已经求过的值即可。int dfs(int x,int y){
if(s[x][y]) return s[x][y];//记忆化搜索
for(int i=0;i<4;i++){
·····
}
然后更新自己的值
s[x][y] = max(s[x][y],s[xx][yy]+1);P 1002 过河卒
所以一个点的方案数 = 左边点的方案数+上方点的方案数
a[i][j] = a[i-1][j]+a[i][j-1];
同时初始化边界第一列和第一行均为1。
之后遍历二维数组,只要所在方格不会被马堵住(令设一个数组标识所有马可以走到的坐标),即可以使用动态转移方程计算。否则为0。
结果dp[n][m]即为所求结果导弹拦截
而需要几套系统能全部拦截,即是求序列的上升子序列的最大长度P4933 大师
dp[i][j]表示以第i项数字结尾的差值为j的等差数列的个数
dp[i][h[i]-h[j]+20000]=(dp[i][h[i]-h[j]+20000]+dp[j][h[i]-h[j]+20000]+1)%mod;
ans = (ans+dp[j][h[i]-h[j]+20000]+1)%mod;
来计算ans,这样可以减少复杂度(比起每次在外层用dp[i]…来计算)
ans = (ans+n)%mod;
+n是:n个只有一个电塔的方案P1233 木棍加工
然后,如果第二维出现上升,即需要另外的加工时间。
因此,对第二维数据进行求最长上升子序列的最大值即为所需的时间。动态规划(区间和环形、树或图)
P1880 石子合并
原来是x1,x2,x3,······,xn
现在变为x1,x2,x3,······,xn,x1,x2,x3,······,xn
复制一遍即可
dp[i][j] = min(dp[i][j],dp[i][k]+dp[k+1][j]+sum[j]-sum[i-1]); for(int len=2;len<=n;len++){
for(int i=1;i+len-1<=2*n;i++){
int j = i+len-1;
for(int k =i;k<j;k++){
dp[i][j] = max(dp[i][j],dp[i][k]+dp[k+1][j]+sum[j]-sum[i-1]);
}
}
}