题解 P1002 【过河卒】

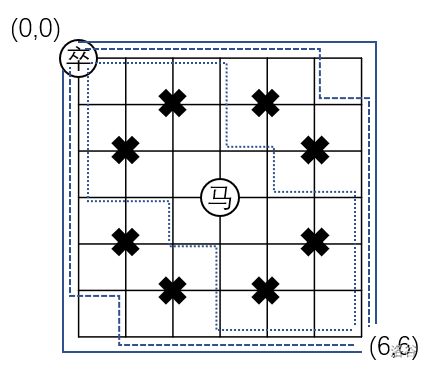
棋盘上 $A$ 点有一个过河卒，需要走到目标 $B$ 点。卒行走的规则：可以向下、或者向右。同时在棋盘上 $C$ 点有一个对方的马，该马所在的点和所有跳跃一步可达的点称为对方马的控制点。因此称之为“马拦过河卒”。

棋盘用坐标表示，$A$ 点 $(0,0)$、$B$ 点 $(n,m)$，同样马的位置坐标是需要给出的。
现在要求你计算出卒从 $A$ 点能够到达 $B$ 点的路径的条数，假设马的位置是固定不动的，并不是卒走一步马走一步。

正文

简单描述一下题意：

士兵想要过河，他每一次可以往下走一格，也可以往右走一格，但马一步走到的地方是不能走的，问走到$n$行，$m$列有多少种走法

我们显然应该先根据马的位置将不能走的格子做一下标记

于是，就会写下这段代码：

void work(long long x,long long y){
    ma[x][y]=1;
    ma[x-1][y-2]=1;
    ma[x-2][y-1]=1;
    ma[x-2][y+1]=1;
    ma[x-1][y+2]=1;
    ma[x+1][y-2]=1;
    ma[x+2][y-1]=1;
    ma[x+2][y+1]=1;
    ma[x+1][y+2]=1;
}

之后就可以使用奥数中的一种简单而常用的方法——标数法

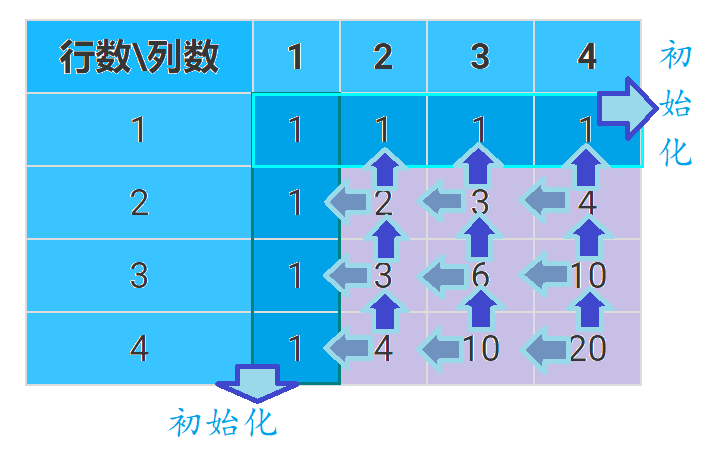
可以举个例子：

从这个表格的第一行第一列，走到第二行第二列的走法数量是由走到第一行第二列的方案数+第二行第一列的方案数

也就是走到x行，y列的方案数=走到x-1行，y列的方案数+走到x行，y-1列的方案数（出界就按0算）

也就是
$$f[i][j]=f[i-1][j]+f[i][j-1]$$

因为走到$x$行$y$列的方案显然是来自于它的左边和它的上面，因为只有这两个格子才可以一步到达这个格子。

于是我们就可以开始递推：

for(int i=1;i<=n;i++){
    for(int j=1;j<=m;j++){
      	if(i==1&&j==1)continue;
       	if(ma[i][j]==0)x[i][j]=x[i-1][j]+x[i][j-1];
    }
}

下面是我AC的代码

#include 
using namespace std;
long long a,b,n,m,x[23][23],ma[23][23];
void work(long long x,long long y){
    ma[x][y]=1;
    ma[x-1][y-2]=1;
    ma[x-2][y-1]=1;
    ma[x-2][y+1]=1;
    ma[x-1][y+2]=1;
    ma[x+1][y-2]=1;
    ma[x+2][y-1]=1;
    ma[x+2][y+1]=1;
    ma[x+1][y+2]=1;
}
int main(){
    scanf("%lld %lld %lld %lld",&n,&m,&a,&b);
    a++;
    b++;
    n++;
    m++;
    work(a,b);
    x[1][1]=1;
    for(int i=1;i<=n;i++){
        for(int j=1;j<=m;j++){
        	if(i==1&&j==1)continue;
        	if(ma[i][j]==0)x[i][j]=x[i-1][j]+x[i][j-1];
        }
    }
    printf("%lld",x[n][m]);
    return 0;
}

后记与补充

观看这张图，我们还可以发现其他的东西，我们能发现下面一行比上一行大的值，就是它左边格子的值，所以，我们可以将这道题优化成一维，代码实现也是很简单的。

$$f[i]+=f[i-1]$$

#include 
using namespace std;
long long a,b,n,m,f[23],ma[23][23];
void work(long long x,long long y){
    ma[x][y]=1;
    ma[x-1][y-2]=1;
    ma[x-2][y-1]=1;
    ma[x-2][y+1]=1;
    ma[x-1][y+2]=1;
    ma[x+1][y-2]=1;
    ma[x+2][y-1]=1;
    ma[x+2][y+1]=1;
    ma[x+1][y+2]=1;
}
int main(){
    scanf("%lld %lld %lld %lld",&n,&m,&a,&b);
    a++;
    b++;
    n++;
    m++;
    work(a,b);
    x[1][1]=1;
    for(int i=1;i<=n;i++)
        for(int j=1;j<=m;j++){
			if(i==1&&j==1)continue;
        	if(ma[i][j]==0)f[j]+=f[j-1];
        }
    printf("%lld",f[m]);
    return 0;
}

如果我的文章对你有帮助请点个赞！！！

谢谢。