leetcode 99. Recover Binary Search Tree 二叉树非递归遍历,利用stack和morris遍历
思路:
一开始觉得就按照二叉搜索树的构造规则由上至下,遇到违反大小规则的节点就直接交换这三个数的值就好了,知道遇到bad case:[3,null,2,null,1],产出结果[2,null,1,null,3],发现这种贪心的策略不work,看了一下tag是用深搜,想了想,从下至上也是一种贪心的策略,也不work的。后来看到讨论区给出in-order的解法,再看看题目,发现还真是巧,因为题目只说交换了两个节点的值,那么只需要找出这两个节点的值,直接换回来就好了,不用还去改其他节点的值。那么怎么找到这两个节点的值呢,这就利用了二叉搜索树in-order序列一定是从小到大的特性,这两个交换了值的节点必定会破坏这个特性,那么这个序列肯定会有两个地方是违反了大小关系的(或者只有一个地方,当这两个节点是相邻的)。两个交换了值的节点里面第一个正确的值是比较小的,第二个正确的值是比较大的,交换之后第一个错误的值是比较大的,第二个错误的值是比较小的,但是第一个节点是在较小子树里面的,第二个节点是在较大子树里面的,那么直接找违反关系的时候,找到第一处违反大小关系地方的较大的数的节点(currentNode)就是第一个节点,第二处违反大小关系地方的较小的数的节点(nextNode)就是第二个节点,或者只发现一处违反大小关系的地方,那么这处地方currentNode就是第一个节点,nextNode就是第二个节点,直接交换currentNode和nextNode里面的值就好了。
递归版inOrder traversal CODE:
struct TreeNode {
int val;
TreeNode *left;
TreeNode *right;
TreeNode(int x) : val(x), left(NULL), right(NULL) {}
};
class Solution {
public:
void recoverTree(TreeNode* root) {
firstPos = NULL, secondPos = NULL, prePtr = NULL;
inOrder(root);
if (firstPos && secondPos) {
int temp = firstPos->val;
firstPos->val = secondPos->val;
secondPos->val = temp;
}
}
private:
void inOrder(TreeNode* root) {
if (!root) {
return;
}
inOrder(root->left);
if (prePtr && prePtr->val > root->val) {
if (!firstPos) {
firstPos = prePtr;
}
secondPos = root;
prePtr = root;
}
inOrder(root->right);
}
TreeNode *firstPos;
TreeNode *secondPos;
TreeNode *prePtr;
};题目给出进阶要求:A solution using O( n ) space is pretty straight forward. Could you devise a constant space solution?
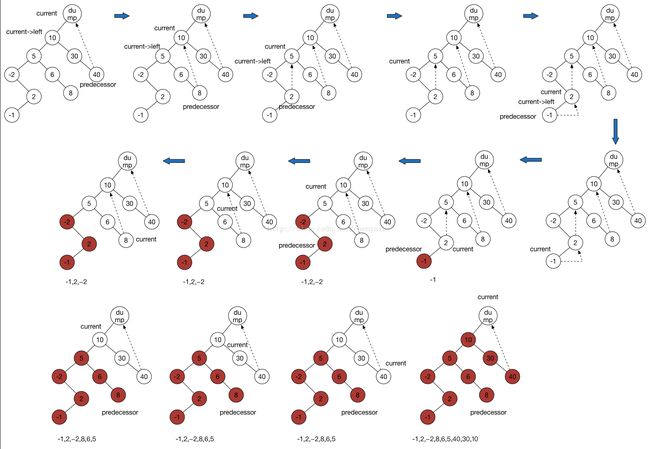
递归版inorder traversal和使用stack的非递归版inorder traversal都是需要O(n)空间复杂度的,有种遍历方法的空间复杂度是O(1)。morris traversal只用到一个指针,遍历的过程中先改变树的结构,最后再改回来。空间复杂度O(1),时间复杂度O(N)。
算法过程:
current = root
while current != NULL
if current->left == NULL //branch1
visit(current)
current = current->right
else //brach2
predecessor = findPredecessor(current)
if predecessor->right == NULL //为了记录左子树的返回点 branch2-1
predecessor->right = current
current = current->left
else //说明左子树已经全部遍历完了 branch2-2
predecessor->right = NULL
visit(current)
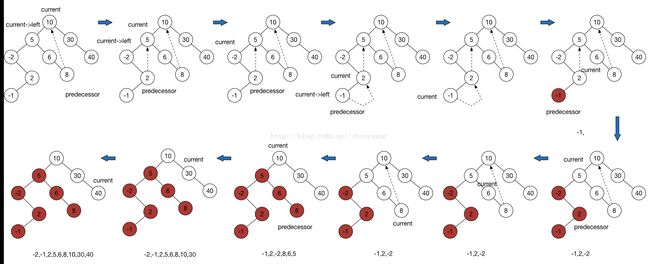
current = current->right例子图解:
二叉搜索树的inorder traversal大致三种做法
- 递归
- stack迭代
- morris traversal
morris traversal只用到一个指针,遍历的过程中先改变树的结构,最后再改回来。空间复杂度O(1),时间复杂度O(N)。
重新整理一次morris traversal的三个版本,分别是preOrder,inOrder,和postOrder。
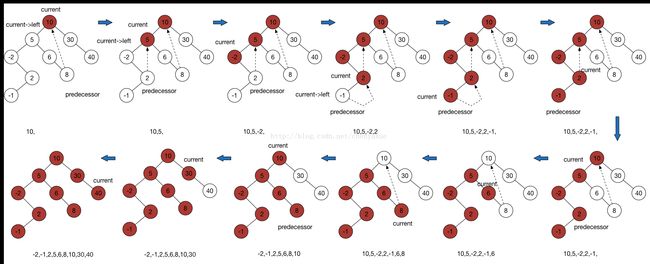
preOrder算法过程:
current = root
while current != NULL
if current->left == NULL //branch1
visit(current)
current = current->right
else //brach2
predecessor = findPredecessor(current)
if predecessor->right == NULL //为了记录左子树的返回点 branch2-1
visit(current) //根节点在左子树被遍历之前就要遍历了
predecessor->right = current
current = current->left
else //说明左子树已经全部遍历完了 branch2-2
predecessor->right = NULL
current = current->right例子图解:
postOrder算法过程:
current = dump
while current != NULL
if current->left == NULL //branch1
current = current->right
else //brach2
predecessor = findPredecessor(current)
if predecessor->right == NULL //为了记录左子树的返回点 branch2-1
predecessor->right = current
current = current->left
else //说明左子树已经全部遍历完了 branch2-2
visit the nodes from predecessor to current->left
//这种visit顺序才能保证左儿子->右儿子->根节点的访问顺序
predecessor->right = NULL
current = current->right例子图解:
第一张图解是没有dump节点的,第二张图解是有dump节点的,以此对比出dump节点在算法中的作用。可以看到第一张图里面根节点的右子树最右的那条路径没有被访问到,所以需要加dump节点,这样的话这条路径的rightmost节点就是dump节点的predecessor,这样的话最后就能被正确访问到。
顺便也整理一下用stack非递归实现的迭代版本的preOrder,inOrder,posOrder traversal
preOrder算法过程:
create an empty stack nodeStack
if root == NULL
return
nodeStack.push(root)
while nodeStack is not empty
current = nodeStack.top()
visit(current)
nodeStack.pop()
if current->right != NULL
nodeStack.push(current->right)
if current->left != NULL
nodeStack.push(current->left)这个算法思路好简单啊,因为visit顺序是根节点->rightChild->leftChild的,所以stack每pop一次,pop出来的就是当前子树的根节点,可以直接输出了,然后在反序处理它的子节点。用一个例子理解一下。

时间复杂度为O(N),因为每个节点都访问了一遍,空间复杂度就是stack的大小,为树的高度O(H),在worst case里H==N,所以空间复杂度也是O(N)。
inOrder的stack算法真是充分利用了stack的特性啊,觉得好巧。关键就是使得每一个从stack那里pop出来的节点都是作为根节点pop出来的,它们的左子树都已经visit过的了。所以遇到节点的左儿子都要先push进栈里面,当节点被pop出来才考虑他的右子树。
inOrder算法过程:
create an empty stack nodeStack
if root == NULL
return
current = root
while true
if current != NULL
nodeStack.push(current)
current = current->left
else
if nodeStack is empty
return
current = nodeStack.top()
nodeStack.pop()
visit(current)
current = current->right
首先讲一下用两个stack实现POSTOrder的算法,这也是充分利用了stack LIFO的特性,根节点先进第一个栈,然后把根节点pop到第二个栈之后再将根节点的左儿子和右儿子push进第一个栈,一直重复这两个操作,这样能保证第二个栈里面根节点肯定是在右儿子的底下,右儿子又肯定是在左儿子的底下,最后将第二个栈里面的内容全部pop出来就得到了POSTOrder的序列。
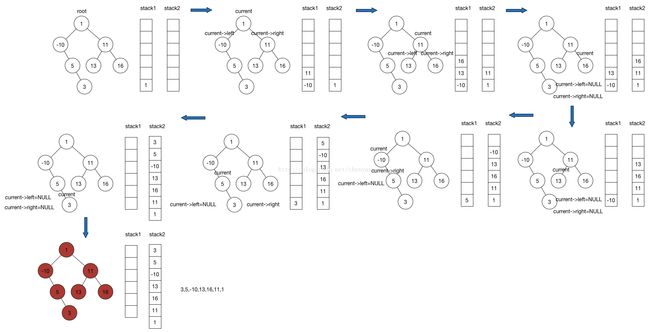
two stack postOrder算法过程:
Create two stacks stack1, stack2
if root == NULL
return
stack1.push(root)
while stack1 is not empty
current = stack1.top()
stack2.push(current)
stack1.pop()
if current->left != NULL
stack1.push(current->left)
if current->right != NULL
stack1.push(current->right)
while stack2 is not empty
current = stack2.top()
visit(current)
stack2.pop()用一个图例帮助理解
用一个stack实现postOrder,先push根节点,如果根节点有左儿子就push根节点的左儿子,如果根节点没有左儿子就找它有没有右儿子,如果根节点有右儿子就就push进去,不然就说明根节点的左子树和右子树都被访问过了,这个时候就可以pop掉根节点,然后判断这个根节点是不是下一个节点的左儿子,如果是的话,就要找下一个节点的右儿子push进去,如果这个根节点是下一个节点的右儿子或者下一个节点没有右儿子,说明下一个节点的子树都已经全部被访问过了,这时可以继续pop下一个节点,继续这个过程直到stack为空。
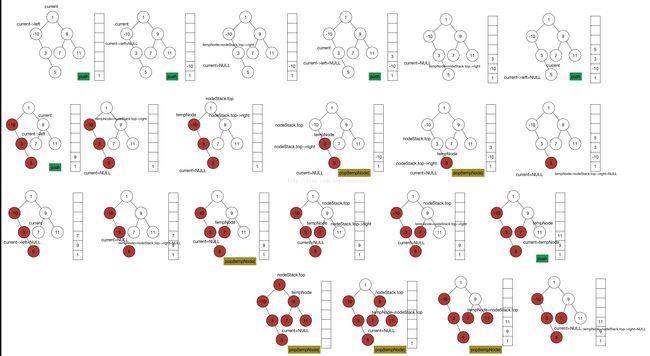
one stack postOrder算法过程:
create a empty stack nodeStack
current = root
while current != NULL || nodeStack is not empty
if current != NULL
nodeStack.push(current)
current = current->left //当前节点如果有左儿子的话一定在当前节点的后面入栈,因为右儿子不能直接跟在左儿子后面入栈,所以打算先处理完当前节点的左子树之后才看它的右子树
else //current == NULL && nodeStack is not empty
tempNode = nodeStack.top()->right
if tempNode == NULL //说明nodeStack.top()的左儿子和右儿子都是空,nodeStack.top()是叶子节点
tempNode = nodeStack.top()
nodeStack.pop()
visit(tempNode)
while nodeStack is not empty && nodeStack.top()->right == tempNode
tempNode = nodeStack.top()
nodeStack.pop()
visit(tempNode)
else
current = tempNode