牛牛打怪兽

链接：https://ac.nowcoder.com/acm/contest/6631/A
来源：牛客网
 

题意

身为屯里第一剑士的牛牛来到训练场里闯关，由于过于勤奋，牛牛的宝剑的耐久度降到了 2 ，这意味着牛牛最多只能打倒两只怪兽，否则将会被淘汰。

训练场的地图可以看作一棵以 1 为根节点的树，训练场的终点为这棵树的叶子结点，树上的每个结点最多有一只怪兽，结点与结点间的边上没有怪兽。

每一个有怪兽的结点上牛牛都需要打倒怪兽才算安全，并且牛牛一旦选定好打怪路线之后便不能走回头路。

请问牛牛有多少种到达终点且不被淘汰的路径。

输入

第一个参数为 n ，(1≤n≤100,000)

第二个参数为大小为 n−1 的点对 (ui​,vi​) 的集合，其中 (ui​,vi​) 表示结点 ui​ 与结点 vi之间有一条边，n1≤ui​,vi​≤n

第三个参数为大小为 n 的 0/1 序列 f ，若 fi​ 为 0 表示i+1结点没有怪兽，否则表示 i+1 结点有怪兽。

返回

一个整数，表示牛牛能到达终点且不被淘汰的路径数。

输入：

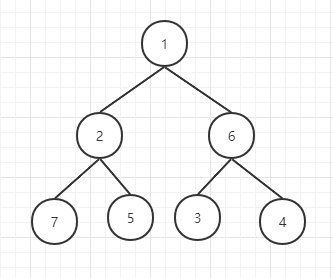
7,[(7,2),(6,1),(5,2),(1,2),(4,6),(6,3)],[0,0,1,0,1,0,0]

输出

4

说明
样例中的四条路径分别为: (1 - 2 - 7), (1 - 2 - 5) , (1 - 6 - 3), (1 - 6 - 4)

 

/**
 * struct Point {
 *	int x;
 *	int y;
 * };
 */

class Solution {
public:
    /**
     * 返回牛牛能到达终点且不被淘汰的路径数
     * @param n int整型 
     * @param Edge Point类vector 
     * @param f int整型vector 
     * @return int整型
     */
    int cnt = 0;
    vector e[100100];
    void dfs(int x , int fa, int num, vector& f){
        int son = 0;
        for(int i = 0; i < e[x].size(); ++i){
            int y = e[x][i];
            if(y == fa) continue;
            son++;
            dfs(y, x, num + f[y - 1], f);
        }
        if(son == 0 && num <= 2) cnt++;
    }
    int solve(int n, vector& Edge, vector& f) {
        // write code here
        for(int i = 0;i < n - 1; i++){
            e[Edge[i].x].push_back(Edge[i].y);
            e[Edge[i].y].push_back(Edge[i].x);
        }
        cnt = 0;
        dfs(1, 0, f[0], f);
        return cnt;
    }
};