HNUCM2020年春季ACM集训队热身赛-第4场题解

问题 A: 字符串最后一个单词的长度

题目描述

计算字符串最后一个单词的长度，单词以空格隔开。

输入

一行字符串，非空，长度小于5000。

输出

整数N，最后一个单词的长度。

样例输入

hello world

样例输出

5

思路

遍历数组维护单词的长度

#include 
using namespace std;
const int maxn=1e5+5;
char s[maxn];
int main()
{
    while(gets(s+1)){
        int ls=strlen(s+1),now=0;
        for(int i=1;i<=ls;++i){
            if(s[i]==' ') now=0;
            else ++now;
        }
        printf("%d\n",now);
    }
    return 0;
}

---

问题 B: 计算字符个数

题目描述

写出一个程序，接受一个ASCII码可见字符组成的字符串，和一个字符，然后输出输入字符串中含有该字符的个数。不区分大小写。

输入

第一行输入一个由ASCII表可见字符组成的字符串(字符串长度<=1e5)，第二行输入一个字符。

输出

输出输入字符串中含有该字符的个数。

样例输入

ABCDEF
A

样例输出

1

思路

既然不区分大小写，就默认全转为小写判断（用tolower函数可以将字符转小写）

#include 
using namespace std;
const int maxn=1e6+5;
char s[maxn];
int main()
{
    char x;
    while(gets(s+1)){
        scanf("%c",&x);
        x=tolower(x);
        int ls=strlen(s+1),ans=0;
        for(int i=1;i<=ls;++i)
            s[i]=tolower(s[i]);
        for(int i=1;i<=ls;++i)
            if(x==s[i])
                ++ans;
        printf("%d\n",ans);
    }
    return 0;
}

---

问题 C: 明明的随机数

题目描述

明明想在学校中请一些同学一起做一项问卷调查，为了实验的客观性，他先用计算机生成了N个1到1000之间的随机整数（N≤1000），对于其中重复的数字，只保留一个，把其余相同的数去掉，不同的数对应着不同的学生的学号。然后再把这些数从小到大排序，按照排好的顺序去找同学做调查。请你协助明明完成“去重”与“排序”的工作(同一个测试用例里可能会有多组数据，希望大家能正确处理)。
Input Param
n 输入随机数的个数
inputArray n个随机整数组成的数组
Return Value
OutputArray 输出处理后的随机整数
注：测试用例保证输入参数的正确性，答题者无需验证。测试用例不止一组。
样例输入解释：
样例有两组测试
第一组是3个数字，分别是：2，2，1。
第二组是11个数字，分别是：10，20，40，32，67，40，20，89，300，400，15。

输入

多组输入，先输入随机整数的个数N(1<=N<=1e5)，再输入相应个数的整数(int范围)。

输出

返回多行，处理后的结果。

样例输入

3
2
2
1
11
10
20
40
32
67
40
20
89
300
400
15

样例输出

1
2
10
15
20
32
40
67
89
300
400

思路

题目的意思是将数组从小到大排序，去重
很容易想到C++的set容器

#include 
using namespace std;
set<int> se;
set<int>::iterator it;
int main()
{
    int n,x;
    while(~scanf("%d",&n)){
        se.clear();
        while(n--){
            scanf("%d",&x);
            se.insert(x);
        }
        for(it=se.begin();it!=se.end();++it){
            printf("%d\n",*it);
        }
    }
    return 0;
}

也可以用sort排序，输出的时候进行判断

#include 
using namespace std;
int a[100005];
int main()
{
    int n;
    while(~scanf("%d",&n)){
        for(int i=1;i<=n;++i)
            scanf("%d",&a[i]);
        sort(a+1,a+n+1);
        for(int i=1;i<=n;++i){
            if(a[i]!=a[i-1]||i==1){//如果是第一个或者和前面的不等就输出
                printf("%d\n",a[i]);
            }
        }
    }
    return 0;
}

---

问题 D: 字符串分隔

题目描述

•连续输入字符串，请按长度为8拆分每个字符串后输出到新的字符串数组；
•长度不是8整数倍的字符串请在后面补数字0，空字符串不处理。

输入

多组输入
每组输入一行字符串(输入2次,每个字符串长度小于100，字符串不包含空格)。

输出

输出到长度为8的新字符串数组。

样例输入

abc
123456789

样例输出

abc00000
12345678
90000000

思路

…还是直接看代码吧

#include 
using namespace std;
char a[205];
int main()
{
    while(~scanf("%s",a+1)){
        int la=strlen(a+1);
        for(int i=la+1;i<=la+8;++i)a[i]='0';//避免判断直接将后面的8个字符赋值为‘0’
        for(int i=1;i<=la;i+=8){
            for(int j=i;j<=i+7;++j){
                printf("%c",a[j]);
            }
            putchar('\n');
        }
    }
    return 0;
}

---

问题 E: 进制转换

题目描述

写出一个程序，接受一个十六进制的数，输出该数值的十进制表示。（多组同时输入 ）

输入

多组输入，每组数据不会超过50条
每组输入一个十六进制的数值字符串n(3<=N<=1e3，N表示字符串长度)。
题目保证十六进制数中的英文字母为大写

输出

输出该数值的十进制字符串。

样例输入

0xA

样例输出

10

思路

数字很大，长度为1e3，要用高精度
而对与16进制转10进制
只需要将答案遍历赋初值为0，遍历16进制，每次将答案乘16再加上16进制这一位的数，即可
例：
1A4=1×16²+10×16¹+4×16⁰=256+160+4=420
如果从左到右遍历
ans=0
ans=ans×16+1=0×16+1=1
ans=ans×16+10=1×16+10=26
ans=ans×16+4=26×16+4=420
证明就略了

#include 
using namespace std;
const int maxn=1e3+5;
char s[maxn];
int ans[10005],lans;
void move(){
    for(int i=1;i<=lans;++i)ans[i]*=16;
    for(int i=1;i<=lans;++i){
        ans[i+1]+=ans[i]/10;
        ans[i]%=10;
    }
    while(ans[lans+1]){
        ++lans;
        ans[lans+1]+=ans[lans]/10;
        ans[lans]%=10;
    }
}
void add(int x){
    ans[1]+=x;
    for(int i=1;i<=lans;++i){
        ans[i+1]+=ans[i]/10;
        ans[i]%=10;
    }
    while(ans[lans+1]){
        ++lans;
        ans[lans+1]+=ans[lans]/10;
        ans[lans]%=10;
    }
}
int main()
{
    while(~scanf("%s",s+1)){
        memset(ans,0,sizeof(ans));
        lans=1;
        int ls=strlen(s+1),x;
        for(int i=3;i<=ls;++i){
            move();//乘16
            if(s[i]>='0'&&s[i]<='9')
                x=s[i]-'0';
            else
                x=s[i]-'A'+10;
            add(x);//加16进制某位的值
        }
        for(int i=lans;i>=1;--i)
            printf("%d",ans[i]);
        putchar('\n');   
    }
    return 0;
}

---

问题 F: Increasing

题目描述

数列A1,A1,…,AN ，修改最少的数字，使得数列严格单调递增。

输入

第 1 行，1 个整数 N 第 2 行，N 个整数 A1,A1,…,AN
。（1 ≤ N ≤ 10^5,1≤ Ai ≤10^9）

输出

1 个整数，表示最少修改的数字 。

样例输入

3
1 2 3

样例输出

0

思路

要保证单调递增，对应数组1 2 9 3 4，9这个不太好处理，要改变前面或后面的才能让9插进去
直接构造比较复杂，需要将问题转化

构造出的数组a[i]和a[i+1]满足a[i+1]>a[i]，而a[i]是整数，那a[i+1]>=a[i]+1
两边减去i+1得a[i+1]-(i+1)>=a[i]-i
设b[i]=a[i]-i
问题也就转变成了经过变换使b数组不下降

而对应不下降的构造比较简单，此时1 2 9 3 4只需要将9变成3或4就可以了
求出最长不下降子序列，修改其他的元素，也就是答案变成n-不下降子序列的长度

二分法求最长不下降子序列

#include 
using namespace std;
const int maxn=1e5+5;
int a[maxn],b[maxn],n;
int main()
{
    while(~scanf("%d",&n)){
        for(int i=1;i<=n;++i){
            scanf("%d",&a[i]);
            a[i]-=i;
        }
        b[1]=a[1];
        int len=1;
        for(int i=2;i<=n;++i){
            if(a[i]>=b[len]){
                b[++len]=a[i];
                continue;
            }
            int mid,l=1,r=len;
            while(l<=r){
                mid=(l+r)>>1;
                if(b[mid]>=a[i]) r=mid-1;
                else l=mid+1;
            }
            b[l]=a[i];
        }
        printf("%d\n",n-len);
    }
    return 0;
}

---

问题 G: Tree

题目描述

给出 N 个点的树和 K，问能否把树划分成 N/K个连通块，且每个连通块的点数都是 K。

输入

第 1 行，1 个整数 T，表示数据组数。接下来 T 组数据，对于每组数据： 第 1 行，2 个整数 N，K。 接下来 (N −1) 行，每行 2 个整数Ai,Bi,表示边(Ai,Bi)点用 1,2,…,N 编号。（1≤T≤10,1≤N,K≤105）

输出

对于每组数据，输出 YES或 NO。

样例输入

2
4 2
1 2
2 3
3 4
4 2
1 2
1 3
1 4

样例输出

YES
NO

思路

一颗树，分成很多个块，每块k个节点
可以dfs自底向上求解

如果以某一个节点为根节点的子树节点数大于k那么说明不能构造
因为该节点每一个子树都小于k（如果大于等于k就在之前便划分出去了）
要使之连通必须将该节点包括进去，就肯定会剩下有一些节点无法用到
如下图，当k=3时，以该节点为根节点的树节点个数为4大于k，黄，蓝，绿三种分法都不满足，肯定有节点会被落下

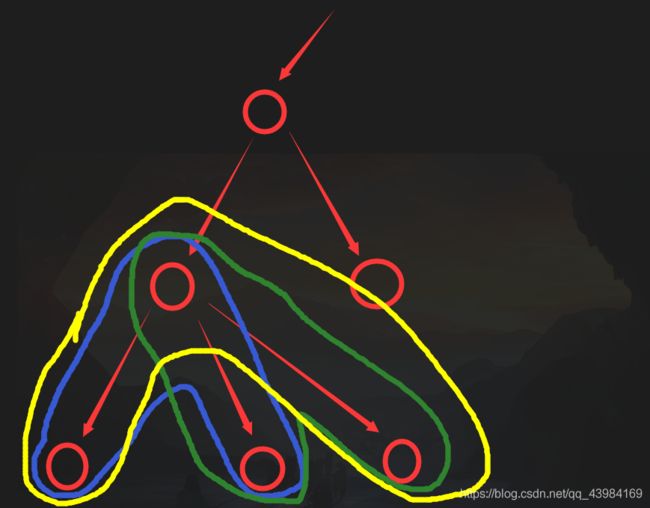
如果以某一个节点为根节点的子树节点数等于k那么直接这部分划分出去

如果以某一个节点为根节点的子树节点数小于k那么并到上面去

#include 
using namespace std;
const int maxn=1e5+5;
struct node{//前向星存图（vector也可以）
    int to,next;
}edge[maxn<<1];
int n,k,head[maxn],cnt,ans;
void add(int a,int b){
    edge[++cnt].to=b;
    edge[cnt].next=head[a];
    head[a]=cnt;
}
int dfs(int now,int fa){ 
    if(!ans)return 0;
    int num=1;
    for(int i=head[now];i!=-1;i=edge[i].next){
        int to=edge[i].to;
        if(to==fa)continue;
        num+=dfs(to,now);
    }
    if(num>k){//不可构造
        ans=0;
        return 0;
    }
    return num%k;
}
int main()
{
    int t,a,b;
    scanf("%d",&t);
    while(t--){
        memset(head,-1,sizeof(head));
        cnt=0,ans=1;
        scanf("%d %d",&n,&k);
        for(int i=1;i<n;++i){
            scanf("%d %d",&a,&b);
            add(a,b),add(b,a);
        }
        dfs(1,0);
        if(ans)printf("YES\n");
        else printf("NO\n");
    }
    return 0;
}

---

问题 H: Lights

题目描述

小 x 有 N 个灯泡，编号从 1 到 N 。灯泡在一开始的时候都是亮着的，小 x 会对这些灯泡进行 M 次操作，每一次操作都会选择一盏灯，并把除了这盏灯以外的灯的开关都按一下（即除了这盏灯以外的所有亮着的灯变成暗的，暗的灯变成亮的）
有趣的是，小 x 只会进行奇数次操作（即 M % 2 == 1），并且最终有且仅有一盏灯是亮着的。
小 y 对小 x 的这一系列操作十分的好奇，她很想知道最后亮着的这一盏灯是哪一盏。所以你能帮助一下她吗？

输入

第一行两个整数N（1≤N≤1018）和M（1≤M≤106）
接下来一行M个整数{a
1
,a
2
,…,a
m
}表示M次操作一次是选择的哪一盏灯。

输出

打印一个整数，表示最后亮着的灯的编号。

样例输入

46 3
1 13 1

样例输出

13

思路

进行m次操作，m是奇数，那么如果一个数被选中奇数次，最后它肯定是亮的，如果被选中偶数次，那最后就是暗的
而题目保证最后只有一个亮的，那就说明只有一个灯被操作了奇数次，也就是只有一个数出现了奇数次
将所有数异或起来就得到了出现奇数次的数（出现偶数次的数异或后为0）

#include 
#define ll long long
using namespace std;
int main()
{
    ll n,ans,x;
    int m;
    while(~scanf("%lld %d",&n,&m)){
        ans=0;
        for(int i=1;i<=m;++i){
            scanf("%lld",&x);
            ans^=x;
        }
        printf("%lld\n",ans);
    }
    return 0;
}