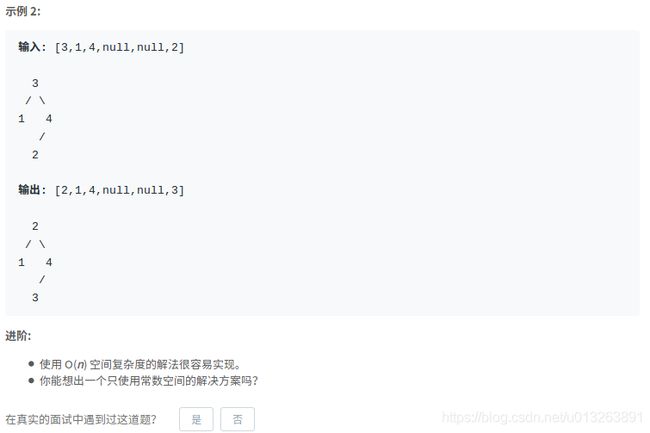
leetcode 99:恢复二叉搜索树

方法一：首先使用中序遍历将所有的节点和节点的值存起来，如果是搜索二叉树节点值的数组应该是升序的，找到不是升序的点，交换节点的值，空间复杂度为O(n)

void inorder(TreeNode*root,std::vector&list,std::vector &vals){
    if(root==NULL)
        return;
    inorder(root->left,list,vals);
    list.push_back(root);
    vals.push_back(root->val);
    inorder(root->right,list,vals);
}

void recoverTree(TreeNode*root){
  std::vectorlist;
  std::vectorvals;
  inorder(root,list,vals);
  std::vector node;
  for(int i=0;ivals[i+1])
      {
          node.push_back(i);
          i=i+2;
          if(node.size()==2)
              break;
      }else
          i=i+1;
  }
  if(node.size()==1)
  {
      int c=node.back();
      node.clear();
      list[c]->val=vals[c+1];
      list[c+1]->val=vals[c];
  }
  else if(node.size()==2){
      int c1=node[0];
      int c2=node[1];
      node.clear();
      list[c1]->val=vals[c2+1];
      list[c2+1]->val=vals[c1];
  }
  sort(vals.begin(),vals.end());
  for(int i=0;ival=vals[i];
}

方法二：使用Morris算法进行遍历，空间复杂度为O(1)

首先介绍Morris算法

1. 当前子树的头结点为head，空闲指针由head的左子树中最右结点的右指针指向head结点。对head的左子树重复该步骤1，直到遍历至某个结点没有左子树，将该结点记    为node。进入步骤2。

2. 从node结点开始通过每个结点的右指针进行移动，并打印结点的值。

  假设遍历到的当前结点为curNode，做如下判断：

curNode结点的左子树中最右结点(记为lastRNode)是否指向curNode。

A. 是 让lastRNode结点的右指针指向null，打印curNode的值。接着通过curNode的右指针遍历下一个结点，重复步骤2。

B. 否 将curNode为头结点的子树重复步骤1。

 

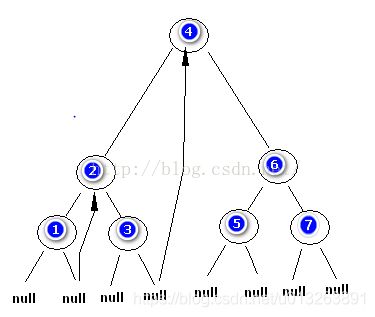
下面举例说明上述步骤(先以中序遍历为例)，二叉树结构如下图所示：

遍历至结点1 发现其没有左子树 记为Node。

curNode : 1 打印1

curNode : 2 满足A 空闲指针由1的右指针指向2 将该空闲指针取消掉 打印2。通过2的右指针遍历到3。

curNode : 3 满足B 进行步骤1 最终打印3。

通过空闲指针遍历至4。

curNode : 4 满足A 空闲指针由3的右指针指向4 将该空闲指针取消掉 打印4。通过4的右指针遍历到6。

至此 左子树和根结点遍历完毕。

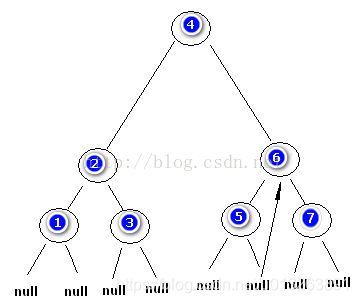
curNode : 6 满足B 进行步骤1 之后二叉树变为右图。

遍历至结点5 其没有左子树 记为Node。

curNode : 5 满足B 进行步骤1 最终打印5。

通过空闲指针遍历至6。

curNode : 6 满足A 空闲指针由5的右指针指向6 将该空闲指针取消掉 打印6。

通过6的右指针遍历到7。

curNode : 7 满足B 进行步骤1 最终打印7。

3. 步骤2最终移动到null结点 整个过程结束。

1) 二叉树的中序遍历

1. 初始化指针cur指向root

2. 当cur不为空时

　 - 如果cur没有左子结点

　     a) 打印出cur的值

　　  b) 将cur指针指向其右子节点

　 - 反之

　    将pre指针指向cur的左子树中的最右子节点　

　　　  * 若pre不存在右子节点

　　　       a) 将其右子节点指回cur

　　　　    b) cur指向其左子节点

　　　  * 反之

　　　　　 a) 将pre的右子节点置空

　　　　　 b) 打印cur的值

　　　　　 c) 将cur指针指向其右子节点

void middle_visit(TreeNode *root) {
    TreeNode*pre;
    TreeNode*cur;
    cur=root;
    while(cur){
        if(cur->left==NULL){
            std::cout<val<right;
        }else
        {
            pre=cur->left;
            while(pre->right!=NULL&&pre->right!=cur){
                pre=pre->right;
            }
            if(pre->right==NULL){
                pre->right=cur;
                cur=cur->left;
            }else{
                pre->right=NULL;
                std::cout<val<right;
            }
        }
    }
}

2)二叉树的前序遍历  前序遍历与中序遍历的差别只是打印的位置不同

1. 初始化指针cur指向root

2. 当cur不为空时

　 - 如果cur没有左子结点

　     a) 打印出cur的值

　　  b) 将cur指针指向其右子节点

　 - 反之

　    将pre指针指向cur的左子树中的最右子节点　

　　　  * 若pre不存在右子节点

　　　       a) 将其右子节点指回cur

                   b) 打印cur的值

　　　　    c) cur指向其左子节点

　　　  * 反之

　　　　　 a) 将pre的右子节点置空

　　　　　 b) 将cur指针指向其右子节点

void pre_visit(TreeNode *root) {
    TreeNode*pre;
    TreeNode*cur;
    cur=root;
    while(cur){
        if(cur->left==NULL){
            std::cout<val<right;
        }else
        {
            pre=cur->left;
            while(pre->right!=NULL&&pre->right!=cur){
                pre=pre->right;
            }
            if(pre->right==NULL){
                pre->right=cur;
                std::cout<val<left;
            }else{
                pre->right=NULL;
                cur=cur->right;
            }
        }
    }
}

3)二叉树的后序遍历 也是打印的的方式不同

1. 初始化指针cur指向root

2. 当cur不为空时

　 - 如果cur没有左子结点

　     a) 打印出cur的值

　　  b) 将cur指针指向其右子节点

　 - 反之

　    将pre指针指向cur的左子树中的最右子节点　

　　　  * 若pre不存在右子节点

　　　       a) 将其右子节点指回cur

　　　　    b) cur指向其左子节点

　　　  * 反之

　　　　　 a) 将pre的右子节点置空

　　　　　 b) 倒序输出从当前节点的左孩子到该前驱节点这条路径上的所有节点。

　　　　　 c) 将cur指针指向其右子节点

 

void reverse(TreeNode*from,TreeNode*to){
    if(from==to)
        return;
    TreeNode *x=from;
    TreeNode*y=from->right;
    TreeNode*z;
    while(true){
        z=y->right;
        y->right=x;
        x=y;
        y=z;
        if(x==to)
            break;
    }
}

void printReverse(TreeNode* from, TreeNode *to) // print the reversed tree nodes 'from' -> 'to'.
{
    reverse(from,to);
    TreeNode*p=to;
    while(true){
        printf("%d",p->val);
        if(p==from)
            break;
        p=p->right;
    }
    reverse(to,from);
}

void post_visit(TreeNode *root) {
    TreeNode dump(0);
    dump.left = root;
    TreeNode *cur = &dump, *prev = NULL;
    while(cur) {
        if (cur->left == NULL) {
            cur = cur->right;
        } else {
            prev = cur->left;
            while (prev->right != NULL && prev->right != cur) {
                prev = prev->right;
            }
            if (prev->right == NULL) {
                prev->right = cur;
                cur = cur->left;
            } else {
                printReverse(cur->left, prev);
                prev->right = NULL;
                cur = cur->right;
            }
        }
    }
}

 

下面是本题方法二的代码，也是使用中序遍历找到两个节点 之后进行交换

void recoverTree(TreeNode *root) {
    TreeNode *first = NULL;//第一个逆序的节点
    TreeNode*second = NULL;//第二个逆序的节点
    TreeNode*parent = NULL;//中序遍历的前一个节点
    TreeNode *cur, *pre;
    cur = root;
    while(cur){
        if(cur->left==NULL){
            if(parent&&parent->val>cur->val){
                if(first==NULL)
                    first=parent;
                second=cur;
            }
            parent=cur;
            cur=cur->right;
        }
        else
        {
            pre=cur->left;
            while(pre->right&&pre->right!=cur)pre=pre->right;
            if(pre->right==NULL){
                pre->right=cur;
                cur=cur->right;
            }
            else
            {
                pre->right=NULL;
                if(parent->val>cur->val)
                {
                    if(first==NULL)
                        first=parent;
                    second=cur;
                }
                parent=cur;
                cur=cur->right;
            }
        }
    }
    if (first && second) swap(first->val, second->val);
}

参考：http://www.cnblogs.com/AnnieKim/archive/2013/06/15/morristraversal.html

https://www.cnblogs.com/ariel-dreamland/p/9159781.html