寒假专题训练——二分

二分思想与一些模板

——二分算法的基本概念——
二分是一种很重要的优化算法，它的作用在于把线性$n$的时间不断折半成$lo{g}_{2}n$的时间，这样处理的目的是最快的求得最优解。


——二分算法的条件——
1.区间符合单调性，即在区间左端点和右端点之间有且只有唯一点$k$，使得位于k两边的区间性质必定不同。
2.需求的解恰好是该区间的临界点$k$。


——二分查找——
二分查找充分利用二分的性质，可以快速从一组单调的数据中找到所需要的位置。
示意图如下(在数列{2,3,5,6,9,10,13,16,20}中快速找到比12大的最小的数字）


——二分模板——
通过上面的简单图解，可以得出二分的基本操作。首先要规定区间的上界和下界，不断对上下界之间的中点进行判断，判断结束后，对区间进行缩小。

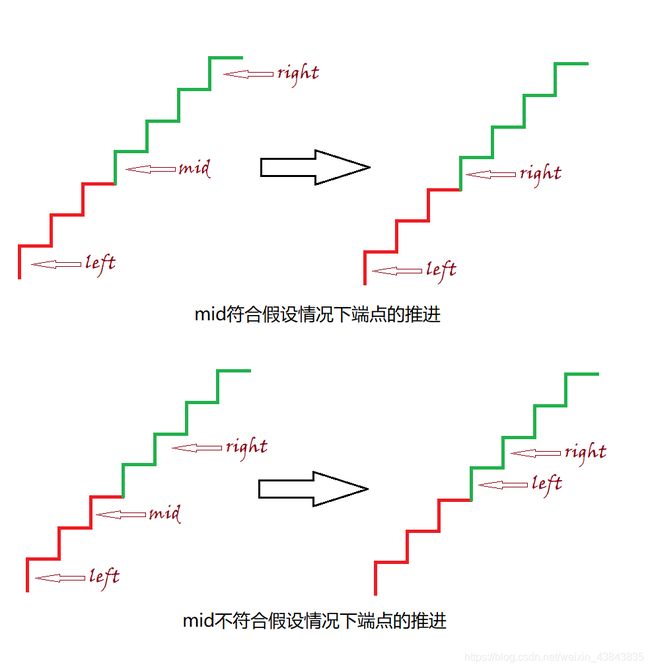
在用二分法时，可以暂时无视条件规定的符合域，假定右区间为符合域(整数型数据，在取mid操作时不会保留小数，如果设左边为符合域，很可能陷入死循环)，最终求得的解再与条件比较。如果正好符合域相反，即取它前一个元素(在数组中取下标小1的元素，连续数则正好-1)。

以下模板:

(int) left=下界,right=上界;
while(left<right)
{
	(int) mid=(left+right)/2;
	if(check(mid)) left=mid+1;
	else right=mid;
}
ans=right or right-1;

当然二分法不仅可以用于整型数，在浮点数上同样起作用，在下面的题目中会涉及到。

T1 小车问题(二分 or 数学解法)

原题链接:P1258 小车问题
洛谷难度评级：普及-


——本题思路——
由于两人同时到达终点，易知两人乘车时间相同，而且问了节省时间，每个人各只乘一次车。


——Code——

#include
#include
#include
#include
#include
using namespace std;
int main()
{
	double s,va,vb,ans;
	scanf("%lf %lf %lf",&s,&va,&vb);
	double left=0,right=s,mid,t1=1551.1551,t2=0.1551;
	while(t1-t2>=0.000001||t1-t2<=-0.000001)
	{
		mid=(left+right)/2;
		double tk=mid/vb;
		double tt=(mid-tk*va)/(va+vb);
		t1=tk+(s-mid)/va;
		t2=tk+tt+(s-(tk+tt)*va)/vb;
		if(t1<t2) right=mid;
		else left=mid;
	}
	printf("%.6lf\n",t1);
	return 0;
}

本题还有一种数学方法，利用解方程的思想，结果直接用常数代入计算(非正道方法，不多概述)。

——Code——

#include
double s,a,b;
int main()
{
	scanf("%lf %lf %lf",&s,&a,&b);
	printf("%.6lf",2*a*s/(3*a*a+a*b)-2*a*s/(3*a*b+b*b)+s/b);
	return 0;	
}

T2 一元三次方程求解(二分+枚举)

题目链接:P1024 一元三次方程求解`
洛谷难度评级:普及/提高-


——本题思路——
注意到题目的条件，解之间的距离严格大于等于$1$，所以可以按照整数点把答案划分成198个区间，求出并比较相邻的区间端点值。如果乘积小于$0$，则对该区间用零点定理。答案要求精确到小数点后两位，所以精度取0.001，保证解的正确性。


——Code——

#include
double a,b,c,d;
double check(double x)
{
	return a*x*x*x+b*x*x+c*x+d;
}
int main()
{
	int i,j,flag=0;
	double ans[3],right,left;
	scanf("%lf %lf %lf %lf",&a,&b,&c,&d);
	for(i=-100;i<100;++i)
	{
		if(check(i)==0)
		{
			ans[flag]=(double)i;
			++flag;
		}
		if(check(i)*check(i+1)<0)
		{
			left=i;
			right=i+1;
			while(right-left>=0.001)
			{
				ans[flag]=(left+right)/2;
				if(check(ans[flag])*check(right)<=0) left=ans[flag];
				else right=ans[flag];
			}
			++flag;
		}
		if(flag==3)
			break;
	}
	for(i=0;i<flag;++i)
		printf("%.2lf ",ans[i]);
	return 0;
}

T3 【模板】最长公共子序列(离散化+贪心+二分)

原题链接:P1439 【模板】最长公共子序列
洛谷难度评级:提高+/省选-


按做正常公共子序列的套路，可以敲出一个时间复杂度$O(n^2)$的算法。


——Code——

#include
#define max(x,y) ((x)>(y)?(x):(y))
int a[100001],b[100001];
int dp[100001]; 
int n;
int main()
{
	int i,j,k;
	while(scanf("%d",&n)!=EOF)
	{
		for(i=0;i<=n;i++)
			dp[i]=0;
		for(i=1;i<=n;++i)
			scanf("%d",&a[i]);
		for(i=1;i<=n;++i)
			scanf("%d",&b[i]);
		for(i=1;i<=n;++i)
		{
			for(j=1;j<=n;++j)
			{
				if(a[i]==b[j])
					dp[j]=dp[j-1]+1;
				else
					dp[j]=max(dp[j],dp[j-1]);
			}
		}
		printf("%d\n",dp[n]);
	}
	return 0;
}

本题给出的答复是50分，AC一半，TLE一半！
本题给出的答复是50分，AC一半，TLE一半！？
本题给出的答复是50分，AC一半，TLE一半？？？
本题给出的答复是50分，AC一半，TLE一半。
本题给出的答复是50分，AC一半，TLE一半… … … …



——本题思路——
这是一道“挂羊头，卖狗肉”的题，和公共子序列没有半毛钱关系。
$n^2$算法会TLE，这说明 无敌的动态规划 对本题不适用。

一、 充分利用全排列的性质:
重新审题，注意到题目的条件，两行序列均为$1$到$n$的全排列，也就是说，第一行会出现的数字，第二行全都会出现。样例第二行序列正好是升序的，也给了一定提示，这道题就是要用最长子序列的方法求。全排列可以这么样，规定一组新的比较大小的规则3<2<1<4<5，那么3相当于原来的1，2还是原来的2，1变成原来的3。依照这个比较规则，对第二行序列进行分析，得出新序列3,2,1,4,5，而这个序列相当于把第一行化为升序数列后第二行序列的等效产物。用图举个例子:

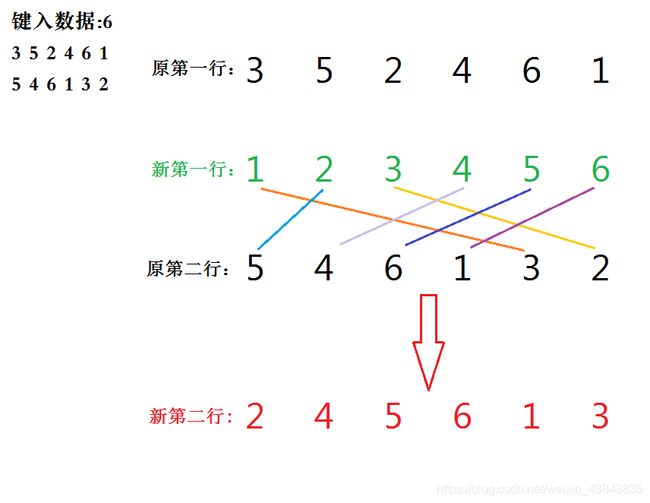
紧接着，对第二行的新序列做一次求最长上升子序列操作。

二、贪心求最长上升子序列
贪心的原则：过程中序列末端的数字要尽量小，这样才有更多机会剩下“大数字”。
每次从序列中遇到一个数，如果它大于当前结尾末端，那么姑且把它装上去。如果小于当前末端，则用二分法快速确定它在序列中的位置，并取代比它大的最小的元素。
合理性：假设这个新元素正好取代末端元素，则符合贪心原则；反之，替换序列中的其它元素，则不会造成任何影响。


综上，时间复杂度$O(nlo{g}_{2}n)$
——Code——

#include
#include
#include
#include
using namespace std;
int s1[100005],s2[100005],dp[100005];
int n;
int main()
{
	int i,j,ans=0,left,right,mid;
	cin>>n;
	memset(s1,0,sizeof(s1));
	memset(s2,0,sizeof(s2));
	memset(dp,0,sizeof(dp));
	for(i=1;i<=n;++i)
	{
		int	k; 
		cin>>k;
		s1[k]=i;
	} 
	for(i=1;i<=n;++i)
	{
		int t;
		cin>>t;
		s2[i]=s1[t];
	}
	for(i=1;i<=n;++i)
	{
		if(dp[ans]<s2[i])
			dp[++ans]=s2[i];
		else
		{
			left=0;
			right=ans;
			while(left<right)
			{
				mid=(left+right)/2;
				if(dp[mid]>s2[i])
					right=mid;
				else
					left=mid+1;
			}
			if(left!=0)
				dp[left]=s2[i];
		}
	}
	cout<<ans<<endl;
	return 0;
} 

这是欺诈！

T4 时间管理(贪心+二分)

本题链接:P2920 [USACO08NOV]时间管理Time Management
洛谷难度评级:普及/提高-


——本题思路——
这题没啥好说的，贪心模板题稍微魔改了一下，就是不用二分从0时刻平推过去也可以。
贪心：根据工作的结束时间进行排序，晚结束的往后推迟，结束时间相同的则优先做时间短的。
二分：初始下界设为0时刻，初始上界设为第一项工作结束时间减去第一件工作时长。


——Code——

#include
#include
#include
#include
using namespace std;
int n;
struct work
{
	int time;
	int deadline;
}a[1001];
bool cmp(struct work p1,struct work p2)
{
	return (p1.deadline==p2.deadline)?(p1.time<p2.time):(p1.deadline<p2.deadline);
}
bool check(int mid)
{
	int i;
	int totalt=mid;
	for(i=0;i<n;++i)
	{
		if(a[i].deadline>=totalt+a[i].time)
			totalt+=a[i].time;
		else
			return 0;
	}
	return 1;
}
int main()
{
	int left,right,mid,ans=0;
	cin>>n;
	for(int i=0;i<n;++i)
		cin>>a[i].time>>a[i].deadline;
	sort(a,a+n,cmp);
	left=0,right=a[0].deadline-a[0].time;
	while(left<=right)
	{
		mid=(left+right)/2;
		if(check(mid))
		{
			ans=mid;
			left=mid+1;
		}
		else
			right=mid-1;
		
	}
	if(!check(0))
		ans=-1;
	cout<<ans<<endl;
	return 0;
}

T5 借教室(差分+二分)

原题链接:P1083 借教室
洛谷难度评级:提高+/省选-


暴力模拟能拿45分！！！
暴力模拟能拿45分！！！
暴力模拟能拿45分！！！
暴力模拟能拿45分！！！
暴力模拟能拿45分！！！


——本题思路——
本题有较多的解法，有空可以都研究一下:
前缀和、线段树、差分…
本专题涉及到二分，那么就想方设法整一个二分的方法出来，实际上也借助了差分来完成。
(差分，前缀和，普通序列时间复杂度的区别)

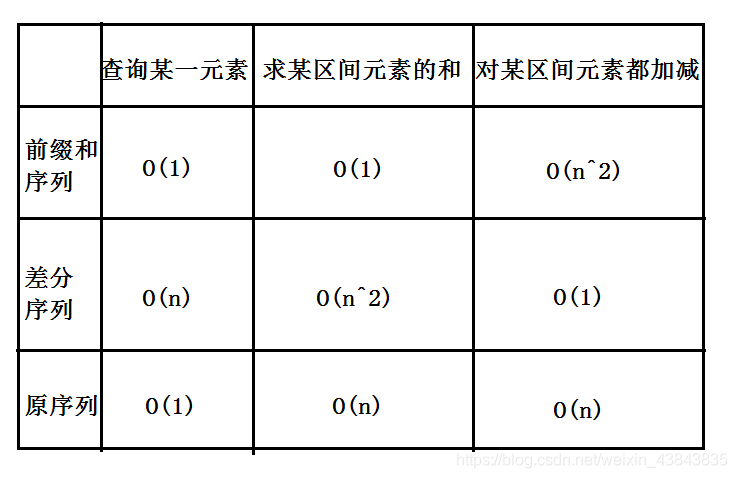
利用差分序列可以在线性时间内排查从订单1到订单k是否满足。订单是否满足具有单调性，一定存在临界状态，大于该状态都不满足，小于该状态都满足，所以对m份订单二分。
完成代码时间复杂度$O(nlo{g}_{2}m)$


——Code——

#include
#include
#include
#include
using namespace std;
long long room[1000005],dr[1000005];
long long ct[1000005],st[1000005],ed[1000005];
int n,m;
bool check(int mid)
{
	int i,j;
	memset(dr,0,sizeof(dr));
	long long judge=0;
	for(i=1;i<=mid;++i)
	{
		dr[st[i]]+=ct[i];
		dr[ed[i]+1]-=ct[i];
	}
	for(i=1;i<=n;++i)
	{
		judge+=dr[i];
		if(judge>room[i])
			return false;
	}
	return true; 
}
int main()
{
	cin>>n>>m;
	int i,j;
	for(i=1;i<=n;++i)
		cin>>room[i];
	for(i=1;i<=m;++i)
		cin>>ct[i]>>st[i]>>ed[i];
	if(check(n))
		 cout<<0<<endl; 
	else
	{
		cout<<-1<<endl;
		int left=1,right=m,mid,ans=0;
		while(left<right)
		{
			mid=(left+right)/2;
			if(check(mid))
				left=mid+1;
			else
				right=mid;
		}
		cout<<right<<endl;
	}
	return 0;
}

牢骚
这题解怎么写着写着就天亮了… … … …