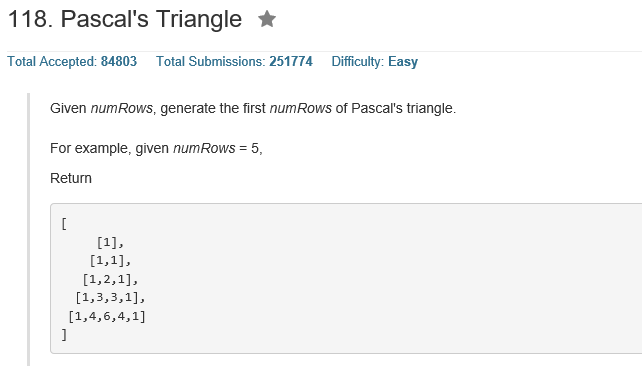
leetcode核心思想:双指针,数字小的那个指针移动classSolution{public:intmaxArea(vector&height){intleft=0;intright=height.size()-1;intmaxArea=0;while(left
leetcode刷题day13|二叉树Part01(递归遍历、迭代遍历、统一迭代、层序遍历)
小冉在学习
leetcode算法职场和发展
递归遍历思路:使用递归的方式比较简单。1、递归函数的传参:因为最后输出一个数组,所以需要传入根节点和一个容器,本来想写数组,但发现长度不能确定,所以选择list。2、终止条件:当访问的节点为空时,return3、递归函数的逻辑:先访问一个节点,递归访问其他节点144.二叉树的前序遍历代码如下:classSolution{publicListpreorderTraversal(TreeNoderoo
leetcode021-合并两个有序链表
陆阳226
问题描述将两个升序链表合并为一个新的升序链表并返回。新链表是通过拼接给定的两个链表的所有节点组成的。示例:输入:1->2->4,1->3->4输出:1->1->2->3->4->4解答递归法:每一层减去一个较小的节点,直到某个链表为null递归结束。publicstaticListNodesolution(ListNodel1,ListNodel2){if(l1==null){returnl2;}
每日一题《leetcode--LCR 022.环形链表||》
Peace & Love487
题目分享leetcode链表算法笔记数据结构
https://leetcode.cn/problems/c32eOV/我们使用两个指针,fast与slow。它们起始都位于链表的头部。随后slow指针每次向后移动一个位置,而fast指针向后移动两个位置。如果链表中存在环,则fast指针最终将再次与slow指针在环中相遇。structListNode*detectCycle(structListNode*head){structListNode*
LCR 078. 合并 K 个升序链表
装B且挨揍の
LeetCode链表算法数据结构经验分享笔记java
https://leetcode.cn/problems/vvXgSW/description/https://leetcode.cn/problems/vvXgSW/description/解题思路方法一:每个链表维护一个索引,每次找到值最小的节点,索引加一。可以采用优先队列实现。/***Definitionforsingly-linkedlist.*publicclassListNode{*i
LeetCode:2390. 从字符串移除*号 使用栈,时间复杂度O(N)
忍界英雄
每日一题leetcodelinux算法
2390.从字符串移除*号today2390.从字符中移除*号题目表述给你一个包含若干星号*的字符串s。在一步操作中,你可以:选中s中的一个星号。移除星号左侧最近的那个非星号字符,并移除该星号自身。返回移除所有星号之后的字符串。注意:生成的输入保证总是可以执行题面中描述的操作。可以证明结果字符串是唯一的。示例1:输入:s=“leet**cod*e”输出:“lecoe”解释:从左到右执行移除操作:距
⭐算法入门⭐《归并排序》简单01 —— LeetCode 21. 合并两个有序链表
英雄哪里出来
《LeetCode算法全集》算法数据结构链表c++归并排序
饭不食,水不饮,题必须刷C语言免费动漫教程,和我一起打卡!《光天化日学C语言》LeetCode太难?先看简单题!《C语言入门100例》数据结构难?不存在的!《数据结构入门》LeetCode太简单?算法学起来!《夜深人静写算法》文章目录一、题目1、题目描述2、基础框架3、原题链接二、解题报告1、思路分析2、时间复杂度3、代码详解三、本题小知识一、题目1、题目描述 将两个不降序链表合并为一个新的不降
【LeetCode 算法笔记】84. 柱状图中最大的矩形
Sardar_
算法leetcode笔记
目录问题描述暴力求解:栈问题描述给定n个非负整数,用来表示柱状图中各个柱子的高度。每个柱子彼此相邻,且宽度为1。求在该柱状图中,能够勾勒出来的矩形的最大面积。示例1:输入:heights=[2,1,5,6,2,3]输出:10解释:最大的矩形为图中红色区域,面积为10示例2:输入:heights=[2,4]输出:4提示:1int:area=0n=len(heights)foriinrange(n):
【LeetCode 算法笔记】739. 每日温度
Sardar_
算法leetcode笔记
目录问题描述暴力解法栈问题描述给定一个整数数组temperatures,表示每天的温度,返回一个数组answer,其中answer[i]是指对于第i天,下一个更高温度出现在几天后。如果气温在这之后都不会升高,请在该位置用0来代替。示例1:输入:temperatures=[73,74,75,71,69,72,76,73]输出:[1,1,4,2,1,1,0,0]示例2:输入:temperatures=
面试题24. 反转链表
阿星啊阿星
反转链表题目描述定义一个函数,输入一个链表的头节点,反转该链表并输出反转后链表的头节点示例:输入:1->2->3->4->5->NULL输出:5->4->3->2->1->NULL提示:0<=节点个数<=5000转载来源:力扣(LeetCode)题目分析1→2→3→null初始化时h为1,now为2,h的next设置成null,有:null←1(h) 2(now)→3现在将保存一下now的next
【数据结构和算法实践-树-LeetCode113-路径总和Ⅱ】
NeVeRMoRE_2024
数据结构与算法实践数据结构算法leetcodeb树
数据结构和算法实践-树-LeetCode113-路径总和Ⅱ题目MyThought代码示例JAVA-8题目给你二叉树的根节点root和一个整数目标和targetSum,找出所有从根节点到叶子节点路径总和等于给定目标和的路径。叶子节点是指没有子节点的节点输入:root=[5,4,8,11,null,13,4,7,2,null,null,5,1],targetSum=22输出:[[5,4,11,2],[
单词搜索 II
xialu
来源:力扣(LeetCode)链接:https://leetcode-cn.com/problems/word-search-ii题目描述:给定一个mxn二维字符网格board和一个单词(字符串)列表words,找出所有同时在二维网格和字典中出现的单词。单词必须按照字母顺序,通过相邻的单元格内的字母构成,其中“相邻”单元格是那些水平相邻或垂直相邻的单元格。同一个单元格内的字母在一个单词中不允许被重
Dom
周华华
JavaScripthtml
<!DOCTYPE html PUBLIC "-//W3C//DTD XHTML 1.0 Transitional//EN" "http://www.w3.org/TR/xhtml1/DTD/xhtml1-transitional.dtd">
<html xmlns="http://www.w3.org/1999/xhtml&q
【Spark九十六】RDD API之combineByKey
bit1129
spark
1. combineByKey函数的运行机制
RDD提供了很多针对元素类型为(K,V)的API,这些API封装在PairRDDFunctions类中,通过Scala隐式转换使用。这些API实现上是借助于combineByKey实现的。combineByKey函数本身也是RDD开放给Spark开发人员使用的API之一
首先看一下combineByKey的方法说明:
msyql设置密码报错:ERROR 1372 (HY000): 解决方法详解
daizj
mysql设置密码
MySql给用户设置权限同时指定访问密码时,会提示如下错误:
ERROR 1372 (HY000): Password hash should be a 41-digit hexadecimal number;
问题原因:你输入的密码是明文。不允许这么输入。
解决办法:用select password('你想输入的密码');查询出你的密码对应的字符串,
然后
路漫漫其修远兮 吾将上下而求索
周凡杨
学习 思索
王国维在他的《人间词话》中曾经概括了为学的三种境界古今之成大事业、大学问者,罔不经过三种之境界。“昨夜西风凋碧树。独上高楼,望尽天涯路。”此第一境界也。“衣带渐宽终不悔,为伊消得人憔悴。”此第二境界也。“众里寻他千百度,蓦然回首,那人却在灯火阑珊处。”此第三境界也。学习技术,这也是你必须经历的三种境界。第一层境界是说,学习的路是漫漫的,你必须做好充分的思想准备,如果半途而废还不如不要开始。这里,注
Hadoop(二)对话单的操作
朱辉辉33
hadoop
Debug:
1、
A = LOAD '/user/hue/task.txt' USING PigStorage(' ')
AS (col1,col2,col3);
DUMP A;
//输出结果前几行示例:
(>ggsnPDPRecord(21),,)
(-->recordType(0),,)
(-->networkInitiation(1),,)
web报表工具FineReport常用函数的用法总结(日期和时间函数)
老A不折腾
finereport报表工具web开发
web报表工具FineReport常用函数的用法总结(日期和时间函数)
说明:凡函数中以日期作为参数因子的,其中日期的形式都必须是yy/mm/dd。而且必须用英文环境下双引号(" ")引用。
DATE
DATE(year,month,day):返回一个表示某一特定日期的系列数。
Year:代表年,可为一到四位数。
Month:代表月份。
c++ 宏定义中的##操作符
墙头上一根草
C++
#与##在宏定义中的--宏展开 #include <stdio.h> #define f(a,b) a##b #define g(a) #a #define h(a) g(a) int main() { &nbs
分析Spring源代码之,DI的实现
aijuans
springDI现源代码
(转)
分析Spring源代码之,DI的实现
2012/1/3 by tony
接着上次的讲,以下这个sample
[java]
view plain
copy
print
for循环的进化
alxw4616
JavaScript
// for循环的进化
// 菜鸟
for (var i = 0; i < Things.length ; i++) {
// Things[i]
}
// 老鸟
for (var i = 0, len = Things.length; i < len; i++) {
// Things[i]
}
// 大师
for (var i = Things.le
网络编程Socket和ServerSocket简单的使用
百合不是茶
网络编程基础IP地址端口
网络编程;TCP/IP协议
网络:实现计算机之间的信息共享,数据资源的交换
协议:数据交换需要遵守的一种协议,按照约定的数据格式等写出去
端口:用于计算机之间的通信
每运行一个程序,系统会分配一个编号给该程序,作为和外界交换数据的唯一标识
0~65535
查看被使用的
JDK1.5 生产消费者
bijian1013
javathread生产消费者java多线程
ArrayBlockingQueue:
一个由数组支持的有界阻塞队列。此队列按 FIFO(先进先出)原则对元素进行排序。队列的头部 是在队列中存在时间最长的元素。队列的尾部 是在队列中存在时间最短的元素。新元素插入到队列的尾部,队列检索操作则是从队列头部开始获得元素。
ArrayBlockingQueue的常用方法:
JAVA版身份证获取性别、出生日期及年龄
bijian1013
java性别出生日期年龄
工作中需要根据身份证获取性别、出生日期及年龄,且要还要支持15位长度的身份证号码,网上搜索了一下,经过测试好像多少存在点问题,干脆自已写一个。
CertificateNo.java
package com.bijian.study;
import java.util.Calendar;
import
【Java范型六】范型与枚举
bit1129
java
首先,枚举类型的定义不能带有类型参数,所以,不能把枚举类型定义为范型枚举类,例如下面的枚举类定义是有编译错的
public enum EnumGenerics<T> { //编译错,提示枚举不能带有范型参数
OK, ERROR;
public <T> T get(T type) {
return null;
【Nginx五】Nginx常用日志格式含义
bit1129
nginx
1. log_format
1.1 log_format指令用于指定日志的格式,格式:
log_format name(格式名称) type(格式样式)
1.2 如下是一个常用的Nginx日志格式:
log_format main '[$time_local]|$request_time|$status|$body_bytes
Lua 语言 15 分钟快速入门
ronin47
lua 基础
-
-
单行注释
-
-
[[
[多行注释]
-
-
]]
-
-
-
-
-
-
-
-
-
-
-
1.
变量 & 控制流
-
-
-
-
-
-
-
-
-
-
num
=
23
-
-
数字都是双精度
str
=
'aspythonstring'
java-35.求一个矩阵中最大的二维矩阵 ( 元素和最大 )
bylijinnan
java
the idea is from:
http://blog.csdn.net/zhanxinhang/article/details/6731134
public class MaxSubMatrix {
/**see http://blog.csdn.net/zhanxinhang/article/details/6731134
* Q35
求一个矩阵中最大的二维
mongoDB文档型数据库特点
开窍的石头
mongoDB文档型数据库特点
MongoDD: 文档型数据库存储的是Bson文档-->json的二进制
特点:内部是执行引擎是js解释器,把文档转成Bson结构,在查询时转换成js对象。
mongoDB传统型数据库对比
传统类型数据库:结构化数据,定好了表结构后每一个内容符合表结构的。也就是说每一行每一列的数据都是一样的
文档型数据库:不用定好数据结构,
[毕业季节]欢迎广大毕业生加入JAVA程序员的行列
comsci
java
一年一度的毕业季来临了。。。。。。。。
正在投简历的学弟学妹们。。。如果觉得学校推荐的单位和公司不适合自己的兴趣和专业,可以考虑来我们软件行业,做一名职业程序员。。。
软件行业的开发工具中,对初学者最友好的就是JAVA语言了,网络上不仅仅有大量的
PHP操作Excel – PHPExcel 基本用法详解
cuiyadll
PHPExcel
导出excel属性设置//Include classrequire_once('Classes/PHPExcel.php');require_once('Classes/PHPExcel/Writer/Excel2007.php');$objPHPExcel = new PHPExcel();//Set properties 设置文件属性$objPHPExcel->getProperties
IBM Webshpere MQ Client User Issue (MCAUSER)
darrenzhu
IBMjmsuserMQMCAUSER
IBM MQ JMS Client去连接远端MQ Server的时候,需要提供User和Password吗?
答案是根据情况而定,取决于所定义的Channel里面的属性Message channel agent user identifier (MCAUSER)的设置。
http://stackoverflow.com/questions/20209429/how-mca-user-i
网线的接法
dcj3sjt126com
一、PC连HUB (直连线)A端:(标准568B):白橙,橙,白绿,蓝,白蓝,绿,白棕,棕。 B端:(标准568B):白橙,橙,白绿,蓝,白蓝,绿,白棕,棕。 二、PC连PC (交叉线)A端:(568A): 白绿,绿,白橙,蓝,白蓝,橙,白棕,棕; B端:(标准568B):白橙,橙,白绿,蓝,白蓝,绿,白棕,棕。 三、HUB连HUB&nb
Vimium插件让键盘党像操作Vim一样操作Chrome
dcj3sjt126com
chromevim
什么是键盘党?
键盘党是指尽可能将所有电脑操作用键盘来完成,而不去动鼠标的人。鼠标应该说是新手们的最爱,很直观,指哪点哪,很听话!不过常常使用电脑的人,如果一直使用鼠标的话,手会发酸,因为操作鼠标的时候,手臂不是在一个自然的状态,臂肌会处于绷紧状态。而使用键盘则双手是放松状态,只有手指在动。而且尽量少的从鼠标移动到键盘来回操作,也省不少事。
在chrome里安装 vimium 插件
MongoDB查询(2)——数组查询[六]
eksliang
mongodbMongoDB查询数组
MongoDB查询数组
转载请出自出处:http://eksliang.iteye.com/blog/2177292 一、概述
MongoDB查询数组与查询标量值是一样的,例如,有一个水果列表,如下所示:
> db.food.find()
{ "_id" : "001", "fruits" : [ "苹
cordova读写文件(1)
gundumw100
JavaScriptCordova
使用cordova可以很方便的在手机sdcard中读写文件。
首先需要安装cordova插件:file
命令为:
cordova plugin add org.apache.cordova.file
然后就可以读写文件了,这里我先是写入一个文件,具体的JS代码为:
var datas=null;//datas need write
var directory=&
HTML5 FormData 进行文件jquery ajax 上传 到又拍云
ileson
jqueryAjaxhtml5FormData
html5 新东西:FormData 可以提交二进制数据。
页面test.html
<!DOCTYPE>
<html>
<head>
<title> formdata file jquery ajax upload</title>
</head>
<body>
<
swift appearanceWhenContainedIn:(version1.2 xcode6.4)
啸笑天
version
swift1.2中没有oc中对应的方法:
+ (instancetype)appearanceWhenContainedIn:(Class <UIAppearanceContainer>)ContainerClass, ... NS_REQUIRES_NIL_TERMINATION;
解决方法:
在swift项目中新建oc类如下:
#import &
java实现SMTP邮件服务器
macroli
java编程
电子邮件传递可以由多种协议来实现。目前,在Internet 网上最流行的三种电子邮件协议是SMTP、POP3 和 IMAP,下面分别简单介绍。
◆ SMTP 协议
简单邮件传输协议(Simple Mail Transfer Protocol,SMTP)是一个运行在TCP/IP之上的协议,用它发送和接收电子邮件。SMTP 服务器在默认端口25上监听。SMTP客户使用一组简单的、基于文本的
mongodb group by having where 查询sql
qiaolevip
每天进步一点点学习永无止境mongo纵观千象
SELECT cust_id,
SUM(price) as total
FROM orders
WHERE status = 'A'
GROUP BY cust_id
HAVING total > 250
db.orders.aggregate( [
{ $match: { status: 'A' } },
{
$group: {
Struts2 Pojo(六)
Luob.
POJOstrust2
注意:附件中有完整案例
1.采用POJO对象的方法进行赋值和传值
2.web配置
<?xml version="1.0" encoding="UTF-8"?>
<web-app version="2.5"
xmlns="http://java.sun.com/xml/ns/javaee&q
struts2步骤
wuai
struts
1、添加jar包
2、在web.xml中配置过滤器
<filter>
<filter-name>struts2</filter-name>
<filter-class>org.apache.st