计算智能——使用遗传算法解决TSP问题
使用遗传算法解决TSP问题
文章目录
- 使用遗传算法解决TSP问题
- 1、TSP问题描述
- 2、遗传算法的介绍
- 2.1、遗传算法简介
- 2.2、遗传算法的原理
- 2.3、遗传算法步骤描述
- 3、代码分析
- 3.1 cross.m
- 3.2 对调函数 exchange.m
- 3.3 适应度函数fit.m
- 3.4变异函数 Mutation.m
- 3.5 染色体的路程代价函数 Mylength.m
- 3.6 连点画图函数 plot_route.m
- 3.7 main.m
- 4、参数调试记录
- 4.1 迭代次数2000,交叉概率为0.8,变异概率为0.05,城市位置不变,种群个数改变
- 4.2 迭代次数2000,变异概率为0.05,城市位置不变,种群个数为150,交叉概率改变
- 4.3 迭代次数2000,城市位置不变,种群个数为150,交叉概率为0.8,变异概率改变
- 4.4 城市位置不变,种群个数为150,交叉概率为0.8,变异概率为0.05,迭代次数改变
- 5、小结
1、TSP问题描述
旅行商(TSP)问题:假设有一个旅行商人要拜访N个城市,要求他从一个城市出发,每个城市最多拜访一次,最后要回到出发的城市,保证所选择的路径长度最短。
2、遗传算法的介绍
2.1、遗传算法简介
遗传算法(Genetic Algorithm, GA)是模拟达尔文生物进化论的自然选择和遗传学机理的生物进化过程的计算模型,是一种通过模拟自然进化过程搜索最优解的方法。
其主要特点是直接对结构对象进行操作,不存在求导和函数连续性的限定;具有内在的隐并行性和更好的全局寻优能力;采用概率化的寻优方法,不需要确定的规则就能自动获取和指导优化的搜索空间,自适应地调整搜索方向。
遗传算法以一种群体中的所有个体为对象,并利用随机化技术指导对一个被编码的参数空间进行高效搜索。其中,选择、交叉和变异构成了遗传算法的遗传操作;参数编码、初始群体的设定、适应度函数的设计、遗传操作设计、控制参数设定五个要素组成了遗传算法的核心内容。
2.2、遗传算法的原理
见https://blog.csdn.net/XYYHHH11/article/details/102899152
首先随机地在父体中选取两个杂交点,并交换相应的段,再根据该段内的城市确定部分映射。 在每个父体上先填入无冲突的城市,而对有冲 突的城市依照映射关系选择候选的城市,直到 找到无冲突的城市填入,按此方法获得了杂交 后的两个后代。
A=9 8 4 | 5 6 7 | 1 3 2 0
B=8 7 1 | 2 3 0 | 9 5 4 6
首先交换A和B的两个匹配区域,得到
A’=9 8 4 | 2 3 0 | l 3 2 0
B’=8 7 1 | 5 6 7 | 9 5 4 6
对于A’、B’两子串中匹配区域以外出现的遍历重复,依据匹配区域内的位置映射关系,逐一进行交换。
对于A’有2到5,3到6,0到7的位置符号映射,对A’的匹配区以外的2,3,0分别以5,6,7 替换,
则得
A”=9 8 4 | 2 3 0 | 1 6 5 7
B”=8 0 1 | 5 6 7 | 9 2 4 3
2.3、遗传算法步骤描述
1、 初始化:设置进化代数计数器iter=0、设置最大迭代次数ITER、交叉概率Pc、变异概率Pmutation、生成种群个数M。
2、个体评价:计算种群中各个个体的适应度。
3、 选择运算:将选择算子作用于群体。以个体适应度为基础,选择最优个体直接遗传到下一代或通过配对交叉产生新的个体再遗传到下一代。
4、交叉运算:在交叉概率的控制下,对群体中的个体两两进行交叉。
5、 变异运算:在变异概率的控制下,对群体中的个体两两进行变异,即对某一个体的基因进行随机调整。
6、 经过选择、交叉、变异运算之后得到下一代群体P1。
重复以上1-6,直到迭代次数为ITER,以进化过程中所得到的具有最大适应度个体作为最优解输出,终止计算。
3、代码分析
3.1 cross.m
function [A,B]=cross(A,B)
L=length(A);
if L<10
W=L;
elseif ((L/10)-floor(L/10))>=rand&&L>10
W=ceil(L/10)+8;
else
W=floor(L/10)+8;
end
p=unidrnd(L-W+1);
fprintf('p=%d ',p);
for i=1:W
x=find(A==B(1,p+i-1));
y=find(B==A(1,p+i-1));
[A(1,p+i-1),B(1,p+i-1)]=exchange(A(1,p+i-1),B(1,p+i-1));
[A(1,x),B(1,y)]=exchange(A(1,x),B(1,y));
end
end
3.2 对调函数 exchange.m
function [x,y]=exchange(x,y)
temp=x;
x=y;
y=temp;
end
3.3 适应度函数fit.m
function fitness=fit(len,m,maxlen,minlen)
fitness=len;
for i=1:length(len)
fitness(i,1)=(1-(len(i,1)-minlen)/(maxlen-minlen+0.0001)).^m;
end
3.4变异函数 Mutation.m
function a=Mutation(A)
index1=0;index2=0;
nnper=randperm(size(A,2));
index1=nnper(1);
index2=nnper(2);
%fprintf('index1=%d ',index1);
%fprintf('index2=%d ',index2);
temp=0;
temp=A(index1);
A(index1)=A(index2);
A(index2)=temp;
a=A;
end
3.5 染色体的路程代价函数 Mylength.m
function len=myLength(D,p)%p是一个排列
[N,NN]=size(D);
len=D(p(1,N),p(1,1));
for i=1:(N-1)
len=len+D(p(1,i),p(1,i+1));
end
end
3.6 连点画图函数 plot_route.m
function plot_route(a,R)
scatter(a(:,1),a(:,2),'rx');
hold on;
plot([a(R(1),1),a(R(length(R)),1)],[a(R(1),2),a(R(length(R)),2)]);
hold on;
for i=2:length(R)
x0=a(R(i-1),1);
y0=a(R(i-1),2);
x1=a(R(i),1);
y1=a(R(i),2);
xx=[x0,x1];
yy=[y0,y1];
plot(xx,yy);
hold on;
end
end
3.7 main.m
%main
clear;
clc;
%%%%%%%%%%%%%%%输入参数%%%%%%%%
N=25; %%城市的个数
M=150; %%种群的个数
ITER=2000; %%迭代次数
%C_old=C;
m=2; %%适应值归一化淘汰加速指数
Pc=0.8; %%交叉概率
Pmutation=0.05; %%变异概率
%%生成城市的坐标
pos=[
1.18532620291447,1.04784532614075;
-0.0305677840415667,0.247645581210592;
-0.616161002689836,-0.952592881020151;
0.446961922684447,-0.169714577770643;
-0.149017967800965,-0.126416340307619;
-0.618495323011524,-0.920741891853885;
0.871553886337660,1.00026002230054;
0.138094617598292,0.489141504610417;
0.499144272753971,0.454575698165666;
-1.45783919493876,-0.0208666762702797;
-0.862108275109509,-0.243060756504686;
0.631710938702084,0.201229520988688;
0.414137360135825,-1.88277836167936;
-0.685461560087154,-2.15635414932313;
0.499385534979484,-1.07925025758297;
0.887584646939535,-1.27957408282239;
0.301813709696180,0.268155563940138;
-1.58614517235173,-0.634534817075024;
-1.64785941090679,-0.0338394169243470;
-1.22878247543605,-0.396878345112974;
0.412046339832314,-0.0656713308136902;
1.22297127364584,-0.448704778091671;
0.825273404809026,1.34828108746778;
0.00627302861462843,-0.0217770670573012;
-0.221274879877384,-0.208054582277596;
];
%%生成城市之间距离矩阵
D=zeros(N,N);
for i=1:N
for j=i+1:N
dis=(pos(i,1)-pos(j,1)).^2+(pos(i,2)-pos(j,2)).^2;
D(i,j)=dis^(0.5);
D(j,i)=D(i,j);
end
end
%%生成初始群体
popm=zeros(M,N);
for i=1:M
popm(i,:)=randperm(N);%随机排列,比如[2 4 5 6 1 3]
end
%%随机选择一个种群
R=popm(1,:);
subplot(2,2,1)
scatter(pos(:,1),pos(:,2),'rx');%画出所有城市坐标
axis([-3 3 -3 3]);
subplot(2,2,2)
plot_route(pos,R); %%画出初始种群对应各城市之间的连线
axis([-3 3 -3 3]);
%%初始化种群及其适应函数
fitness=zeros(M,1);
len=zeros(M,1);
for i=1:M%计算每个染色体对应的总长度
len(i,1)=myLength(D,popm(i,:));
end
maxlen=max(len);%最大回路
minlen=min(len);%最小回路
fitness=fit(len,m,maxlen,minlen);
rr=find(len==minlen);%找到最小值的下标,赋值为rr
R=popm(rr(1,1),:);%提取该染色体,赋值为R
for i=1:N
fprintf('%d ',R(i));%把R顺序打印出来
end
fprintf('\n');
fitness=fitness/sum(fitness);
distance_min=zeros(ITER+1,1); %%各次迭代的最小的种群的路径总长
nn=M;
iter=0;
while iter<=ITER
fprintf('迭代第%d次\n',iter);
%%选择操作
p=fitness./sum(fitness);
q=cumsum(p);%累加
for i=1:(M-1)
len_1(i,1)=myLength(D,popm(i,:));
r=rand;
tmp=find(r<=q);
popm_sel(i,:)=popm(tmp(1),:);
end
[fmax,indmax]=max(fitness);%求当代最佳个体
popm_sel(M,:)=popm(indmax,:);
%%交叉操作
nnper=randperm(M);
% A=popm_sel(nnper(1),:);
% B=popm_sel(nnper(2),:);
%%
for i=1:M*Pc*0.5
A=popm_sel(nnper(i),:);
B=popm_sel(nnper(i+1),:);
[A,B]=cross(A,B);
% popm_sel(nnper(1),:)=A;
% popm_sel(nnper(2),:)=B;
popm_sel(nnper(i),:)=A;
popm_sel(nnper(i+1),:)=B;
end
%%变异操作
for i=1:M
pick=rand;
while pick==0
pick=rand;
end
if pick<=Pmutation
popm_sel(i,:)=Mutation(popm_sel(i,:));
end
end
%%求适应度函数
NN=size(popm_sel,1);
len=zeros(NN,1);
for i=1:NN
len(i,1)=myLength(D,popm_sel(i,:));
end
maxlen=max(len);
minlen=min(len);
distance_min(iter+1,1)=minlen;
fitness=fit(len,m,maxlen,minlen);
rr=find(len==minlen);
fprintf('minlen=%d\n',minlen);
R=popm_sel(rr(1,1),:);
for i=1:N
fprintf('%d ',R(i));
end
fprintf('\n');
popm=[];
popm=popm_sel;
iter=iter+1;
%pause(1);
end
%end of while
subplot(2,2,3)
plot_route(pos,R);
axis([-3 3 -3 3]);
subplot(2,2,4)
plot(distance_min);
4、参数调试记录
遗传算法有几个重要参数:
交叉概率Pc
变异概率Pmutation
城市位置(存储在pos中)和个数N
种群个数M
4.1 迭代次数2000,交叉概率为0.8,变异概率为0.05,城市位置不变,种群个数改变

其他参数不变的前提下,当种群数量M=150的时候最短距离最短,并且收敛速度最快。
4.2 迭代次数2000,变异概率为0.05,城市位置不变,种群个数为150,交叉概率改变
②、交叉概率为0.2

③、交叉概率为0.4


④、交叉概率为0.6


⑤、交叉概率为0.8
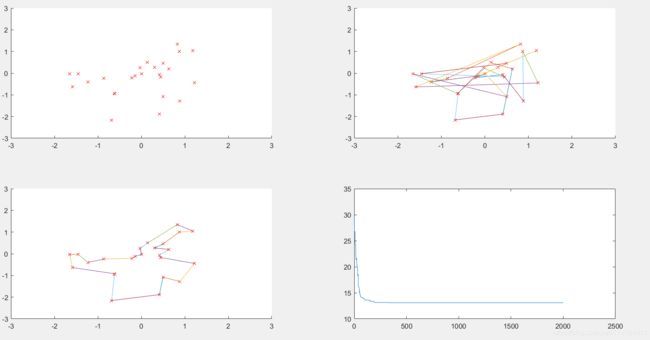

其他参数不变的前提下,如果交叉概率为0的话,最短路径特别大,而且收敛也比其他慢。而随着交叉概率变大,函数收敛越来越快,当交叉概率为0.8,找到了最优解。
4.3 迭代次数2000,城市位置不变,种群个数为150,交叉概率为0.8,变异概率改变
①、变异概率为0.01


②、变异概率为0.03


③、变异概率为0.05


④、变异概率为0.07
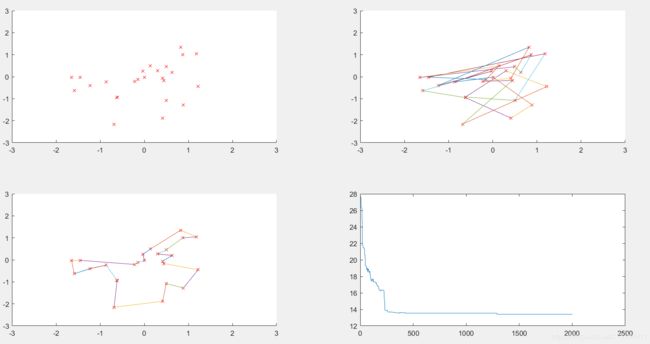

⑤、变异概率为0.09
在其他参数不变的情况下,变异概率为0.03时,最短路径最小,同时收敛速度也最快。随着变异概率的增大,收敛速度先变快后变慢。 变异概率太大反而会使得最短路径增加。
4.4 城市位置不变,种群个数为150,交叉概率为0.8,变异概率为0.05,迭代次数改变
①、迭代次数500


②、迭代次数1000


③、迭代次数1500


④、迭代次数2000


⑤、迭代次数2500

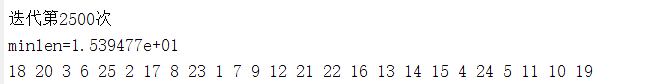
当其他参数不变时当迭代次数为1500时,所求路径最短。当迭代次数500次的时候的时候虽然最小值也很小,但是500的时候在快到结束的时候还在波动。所以应该在之前的实验中把迭代次数设为1500左右就好。
四.遗传算法与蚁群算法的对比分析
对于两个算法的分析比较,我采取的方法是,在两种方法都用之前是实验出的较优参数的情况下,改变城市的数量。让两个算法运行相同城市数量时的数据集对比算法的速度和最优值和最差值的差。来看什么时候用哪个算法更合适。
5、小结
1、蚁群算法基于信息素在环境中的指示,遗传算法是基于优胜劣汰的生物进化思想
2、遗传算法得到的结果会受到交叉概率、变异概率、迭代次数的影响:当交叉概率为0.8,变异概率为0…03,结果相对来说会稍微好一些。
3、用遗传算法来求解TSP问题的速度要比用蚁群算法来解决TSP问题快的多,但迭代次数会多很多。
4、遗传算法有交叉,变异等不同算子,每种算子又有各自的不同方法,通过对算子方法的修改,可以得到不同的改进遗传算法,而蚁群算法则可以通过设定精英蚂蚁来改进算法。