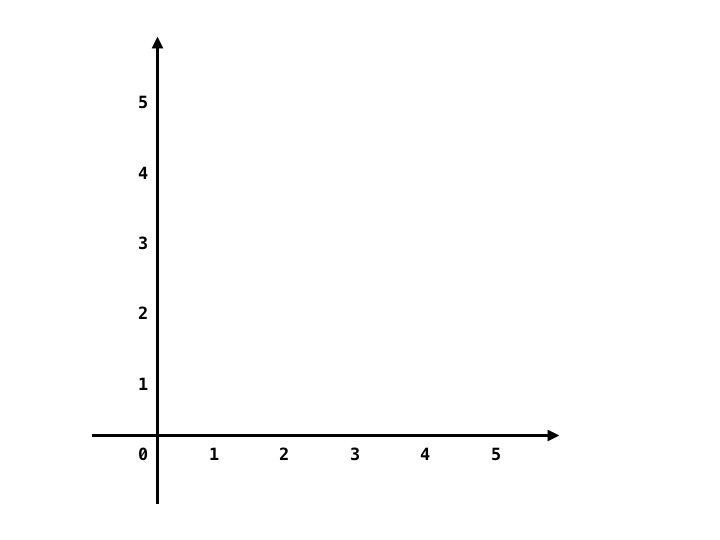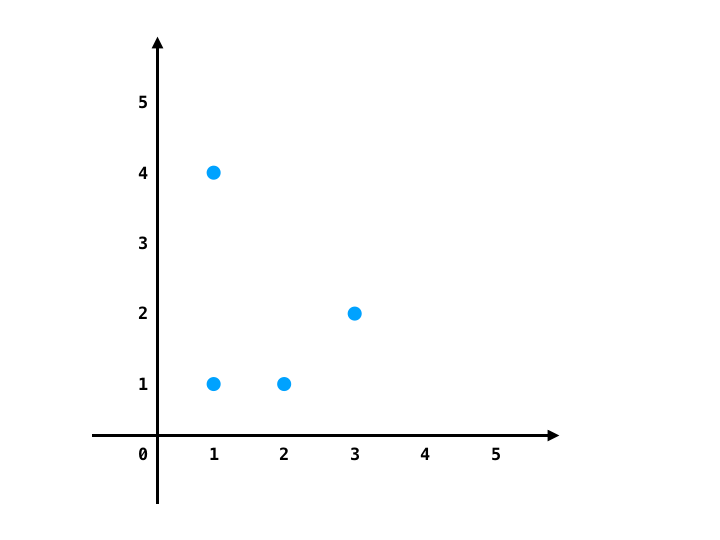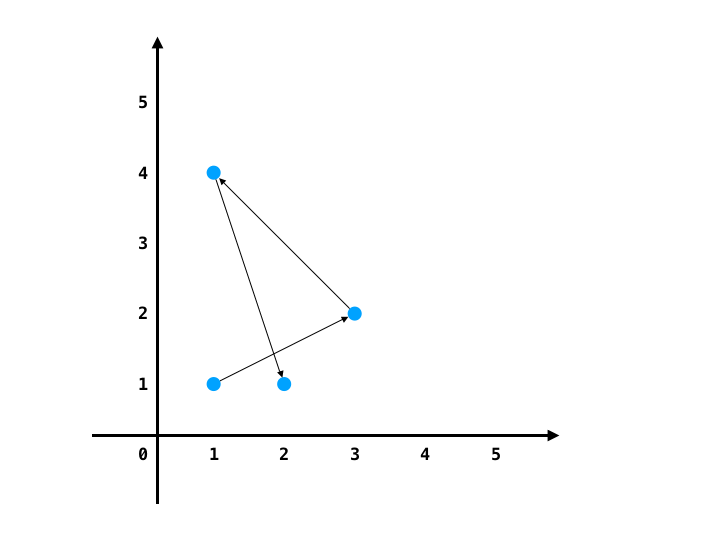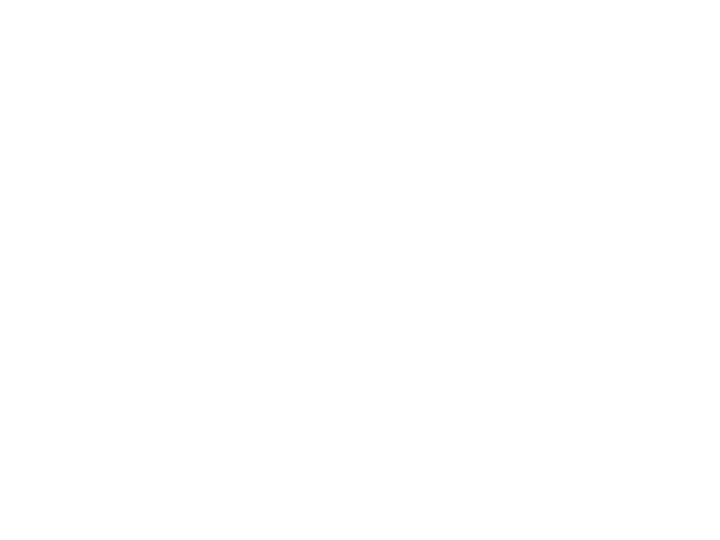2020 Leetcode 春季赛战队赛 题目汇总
1. 期望个数统计
某互联网公司一年一度的春招开始了,一共有 n 名面试者入选。每名面试者都会提交一份简历,公司会根据提供的简历资料产生一个预估的能力值,数值越大代表越有可能通过面试。
小 A 和小 B 负责审核面试者,他们均有所有面试者的简历,并且将各自根据面试者能力值从大到小的顺序浏览。由于简历事先被打乱过,能力值相同的简历的出现顺序是从它们的全排列中等可能地取一个。现在给定 n 名面试者的能力值 scores,设 X 代表小 A 和小 B 的浏览顺序中出现在同一位置的简历数,求 X 的期望。
提示:离散的非负随机变量的期望计算公式为 。在本题中,由于 X 的取值为 0 到 n 之间,期望计算公式可以是 。
示例 1:
输入:
scores = [1,2,3]输出:
3解释:由于面试者能力值互不相同,小 A 和小 B 的浏览顺序一定是相同的。
X的期望是 3 。
示例 2:
输入:
scores = [1,1]输出:
1解释:设两位面试者的编号为 0, 1。由于他们的能力值都是 1,小 A 和小 B 的浏览顺序都为从全排列
[[0,1],[1,0]]中等可能地取一个。如果小 A 和小 B 的浏览顺序都是[0,1]或者[1,0],那么出现在同一位置的简历数为 2 ,否则是 0 。所以X的期望是 (2+0+2+0) * 1/4 = 1
示例 3:
输入:
scores = [1,1,2]输出:
2
限制:
1 <= scores.length <= 10^50 <= scores[i] <= 10^6
2. 小张刷题计划
为了提高自己的代码能力,小张制定了 LeetCode 刷题计划,他选中了 LeetCode 题库中的 n 道题,编号从 0 到 n-1,并计划在 m 天内按照题目编号顺序刷完所有的题目(注意,小张不能用多天完成同一题)。
在小张刷题计划中,小张需要用 time[i] 的时间完成编号 i 的题目。此外,小张还可以使用场外求助功能,通过询问他的好朋友小杨题目的解法,可以省去该题的做题时间。为了防止“小张刷题计划”变成“小杨刷题计划”,小张每天最多使用一次求助。
我们定义 m 天中做题时间最多的一天耗时为 T(小杨完成的题目不计入做题总时间)。请你帮小张求出最小的 T是多少。
示例 1:
输入:
time = [1,2,3,3], m = 2输出:
3解释:第一天小张完成前三题,其中第三题找小杨帮忙;第二天完成第四题,并且找小杨帮忙。这样做题时间最多的一天花费了 3 的时间,并且这个值是最小的。
示例 2:
输入:
time = [999,999,999], m = 4输出:
0解释:在前三天中,小张每天求助小杨一次,这样他可以在三天内完成所有的题目并不花任何时间。
限制:
1 <= time.length <= 10^51 <= time[i] <= 100001 <= m <= 1000
3. 寻宝
我们得到了一副藏宝图,藏宝图显示,在一个迷宫中存在着未被世人发现的宝藏。
迷宫是一个二维矩阵,用一个字符串数组表示。它标识了唯一的入口(用 'S' 表示),和唯一的宝藏地点(用 'T' 表示)。但是,宝藏被一些隐蔽的机关保护了起来。在地图上有若干个机关点(用 'M' 表示),只有所有机关均被触发,才可以拿到宝藏。
要保持机关的触发,需要把一个重石放在上面。迷宫中有若干个石堆(用 'O' 表示),每个石堆都有无限个足够触发机关的重石。但是由于石头太重,我们一次只能搬一个石头到指定地点。
迷宫中同样有一些墙壁(用 '#' 表示),我们不能走入墙壁。剩余的都是可随意通行的点(用 '.' 表示)。石堆、机关、起点和终点(无论是否能拿到宝藏)也是可以通行的。
我们每步可以选择向上/向下/向左/向右移动一格,并且不能移出迷宫。搬起石头和放下石头不算步数。那么,从起点开始,我们最少需要多少步才能最后拿到宝藏呢?如果无法拿到宝藏,返回 -1 。
示例 1:
输入: ["S#O", "M..", "M.T"]
输出:16
解释:最优路线为: S->O, cost = 4, 去搬石头 O->第二行的M, cost = 3, M机关触发 第二行的M->O, cost = 3, 我们需要继续回去 O 搬石头。 O->第三行的M, cost = 4, 此时所有机关均触发 第三行的M->T, cost = 2,去T点拿宝藏。 总步数为16。
示例 2:
输入: ["S#O", "M.#", "M.T"]
输出:-1
解释:我们无法搬到石头触发机关
示例 3:
输入: ["S#O", "M.T", "M.."]
输出:17
解释:注意终点也是可以通行的。
限制:
1 <= maze.length <= 1001 <= maze[i].length <= 100maze[i].length == maze[j].length- S 和 T 有且只有一个
- 0 <= M的数量 <= 16
- 0 <= O的数量 <= 40,题目保证当迷宫中存在 M 时,一定存在至少一个 O 。
4. 切分数组
给定一个整数数组 nums ,小李想将 nums 切割成若干个非空子数组,使得每个子数组最左边的数和最右边的数的最大公约数大于 1 。为了减少他的工作量,请求出最少可以切成多少个子数组。
示例 1:
输入:
nums = [2,3,3,2,3,3]输出:
2解释:最优切割为 [2,3,3,2] 和 [3,3] 。第一个子数组头尾数字的最大公约数为 2 ,第二个子数组头尾数字的最大公约数为 3 。
示例 2:
输入:
nums = [2,3,5,7]输出:
4解释:只有一种可行的切割:[2], [3], [5], [7]
限制:
1 <= nums.length <= 10^52 <= nums[i] <= 10^6
5. 游乐园的迷宫
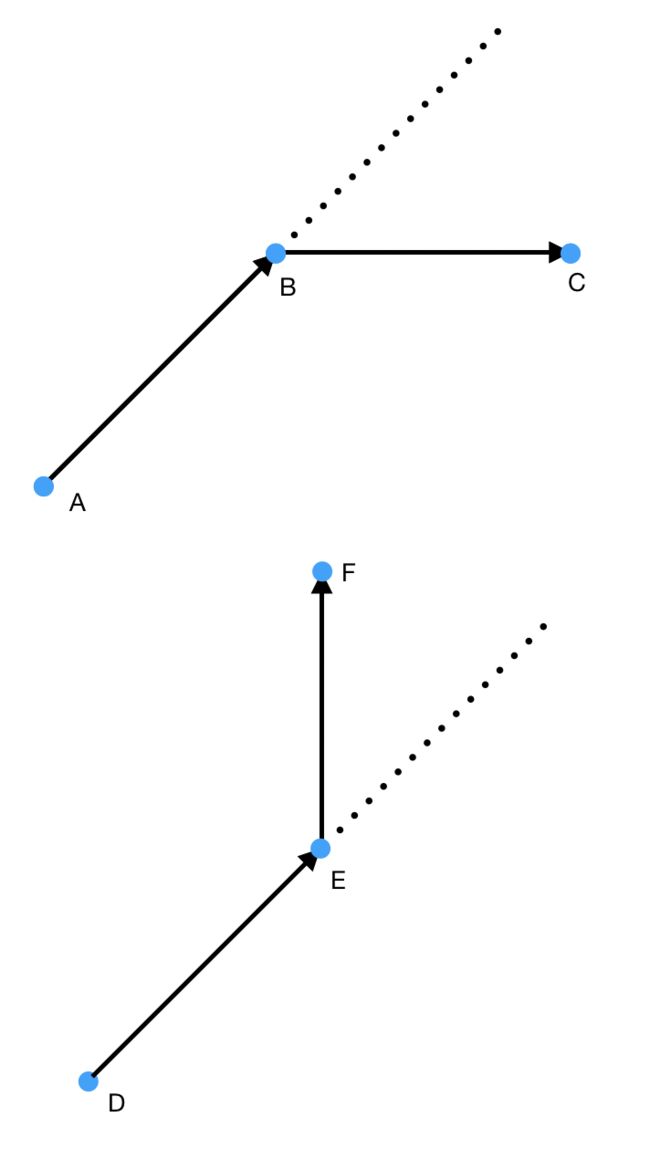
小王来到了游乐园,她玩的第一个项目是模拟推销员。有一个二维平面地图,其中散布着 N 个推销点,编号 0 到 N-1,不存在三点共线的情况。每两点之间有一条直线相连。游戏没有规定起点和终点,但限定了每次转角的方向。首先,小王需要先选择两个点分别作为起点和终点,然后从起点开始访问剩余 N-2 个点恰好一次并回到终点。访问的顺序需要满足一串给定的长度为 N-2 由 L 和 R 组成的字符串 direction,表示从起点出发之后在每个顶点上转角的方向。根据这个提示,小王希望你能够帮她找到一个可行的遍历顺序,输出顺序下标(若有多个方案,输出任意一种)。可以证明这样的遍历顺序一定是存在的。
(上图:A->B->C 右转; 下图:D->E->F 左转)
示例 1:
输入:
points = [[1,1],[1,4],[3,2],[2,1]], direction = "LL"输入:
[0,2,1,3]解释:[0,2,1,3] 是符合"LL"的方案之一。在 [0,2,1,3] 方案中,0->2->1 是左转方向, 2->1->3 也是左转方向
示例 2:
输入:
points = [[1,3],[2,4],[3,3],[2,1]], direction = "LR"输入:
[0,3,1,2]解释:[0,3,1,2] 是符合"LR"的方案之一。在 [0,3,1,2] 方案中,0->3->1 是左转方向, 3->1->2 是右转方向
限制:
3 <= points.length <= 1000 且 points[i].length == 21 <= points[i][0],points[i][1] <= 10000direction.length == points.length - 2direction 只包含 "L","R"
6. 游乐园的游览计划
又到了一年一度的春游时间,小吴计划去游乐场游玩 1 天,游乐场总共有 N 个游乐项目,编号从 0 到 N-1。小吴给每个游乐项目定义了一个非负整数值 value[i] 表示自己的喜爱值。两个游乐项目之间会有双向路径相连,整个游乐场总共有 M 条双向路径,保存在二维数组 edges中。 小吴计划选择一个游乐项目 A 作为这一天游玩的重点项目。上午小吴准备游玩重点项目 A 以及与项目 A 相邻的两个项目 B、C (项目A、B与C要求是不同的项目,且项目B与项目C要求相邻),并返回 A ,即存在一条 A-B-C-A 的路径。 下午,小吴决定再游玩重点项目 A以及与A相邻的两个项目 B'、C',(项目A、B'与C'要求是不同的项目,且项目B'与项目C'要求相邻),并返回 A ,即存在一条 A-B'-C'-A 的路径。下午游玩项目 B'、C' 可与上午游玩项目B、C存在重复项目。 小吴希望提前安排好游玩路径,使得喜爱值之和最大。请你返回满足游玩路径选取条件的最大喜爱值之和,如果没有这样的路径,返回 0。 注意:一天中重复游玩同一个项目并不能重复增加喜爱值了。例如:上下午游玩路径分别是 A-B-C-A与A-C-D-A 那么只能获得 value[A] + value[B] + value[C] + value[D] 的总和。
示例 1:
输入:
edges = [[0,1],[1,2],[0,2]], value = [1,2,3]输出:
6解释:喜爱值之和最高的方案之一是 0->1->2->0 与 0->2->1->0 。重复游玩同一点不重复计入喜爱值,返回1+2+3=6
示例 2:
输入:
edges = [[0,2],[2,1]], value = [1,2,5]输出:
0解释:无满足要求的游玩路径,返回 0
示例 3:
输入:
edges = [[0,1],[0,2],[0,3],[0,4],[0,5],[1,3],[2,4],[2,5],[3,4],[3,5],[4,5]], value = [7,8,6,8,9,7]输出:
39解释:喜爱值之和最高的方案之一是 3->0->1->3 与 3->4->5->3 。喜爱值最高为 7+8+8+9+7=39
限制:
3 <= value.length <= 100001 <= edges.length <= 100000 <= edges[i][0],edges[i][1] < value.length0 <= value[i] <= 10000edges中没有重复的边edges[i][0] != edges[i][1]