Interactive Structure-aware Blending of Diverse Edge Bundling Visualizations
论文传送门
视频
论文主页
作者
山东大学
- Yunhai Wang
- Mingliang Xue
- Yanyan Wang
- Xinyuan Yan
北京大学 - Baoquan Chen
香港中文大学 - Chi-Wing Fu
法国国立民航大学 - Christophe Hurter
摘要
存在许多边捆绑技术(即简化数据以支持数据可视化和决策),但是它们不能直接应用于任何类型的数据集,并且它们的参数通常过于抽象并且难以设置。结果,这阻碍了用户创建有效的聚合可视化效果的能力。为了解决这一问题,我们研究了一种以任务驱动和以用户为中心的方法来处理视觉聚合的新颖方法。给定一个图形,我们的方法将产生一个杂乱的视图,如下所示:首先,用户研究不同的边绑定结果,并指定某些边绑定技术将提供用户所需结果的区域。其次,我们的系统然后计算这些指定区域之间的平滑且结构保留的过渡。最后,用户可以使用直接操作技术进一步微调全局可视化效果,以消除局部歧义并应用不同的视觉变形。在本文中,我们提供了设计原理和实现的详细信息。此外,我们展示了与当前的边捆绑技术相比,我们的算法如何提供更合适的结果,最后,我们提供了用法的具体实例,其中算法结合了各种边绑定结果以支持各种数据探索和可视化。
Introduction
-
Force-Directed Edge Bundling
-
Skeleton-Based Edge Bundling
-
KDE Based Edge Bundling
-
Geometry-Based Edge-Bundling
-
现有不足:
-
It’s difficult to find suitable parameters.
-
One method might not be enough.
Idea: Blending for exploration
- Direct Combination (Distortions)
- Further Apply Laplacian Smoothing (The Bundled area becomes loose)
Related Work
MoleView
Design Rationales
- DR1: preservation of the inherent visual data structure
- DR2: smooth transition between different aggregated areas to avoid large distortion
- DR3: ensure readability of the graph structures, especially for the regions of interest, and
- DR4: flexible fine-tuning of the end result
goal: a smooth, coherent and ambiguity-free blending result
Framework
arg min Z ∑ ( l , i ) ∈ U \ S α ∥ z l , i − x l , i ∥ 2 \arg \min _{\mathbf{Z}} \sum_{(l, i) \in \mathbf{U} \backslash \mathbf{S}} \alpha\left\|\mathbf{z}_{l, i}-\mathbf{x}_{l, i}\right\|^{2} argminZ∑(l,i)∈U\Sα∥zl,i−xl,i∥2
+ ∑ ( l , i ) ∈ S β ∥ z l , i − z l , i + 1 − d l , i l , i + 1 ∥ 2 \quad+\sum_{(l, i) \in \mathbf{S}} \beta\left\|\mathbf{z}_{l, i}-\mathbf{z}_{l, i+1}-\mathbf{d}_{l, i}^{l, i+1}\right\|^{2} +∑(l,i)∈Sβ∥∥∥zl,i−zl,i+1−dl,il,i+1∥∥∥2
+ ∑ ( l , i ) ∈ C θ ∥ ( 1 − μ l , i ) z l , i − 1 + μ l , i z l , i + 1 − z l , i ∥ 2 \quad+\sum_{(l, i) \in \mathbf{C}} \theta\left\|\left(1-\mu_{l, i}\right) \mathbf{z}_{l, i-1}+\mu_{l, i} \mathbf{z}_{l, i+1}-\mathbf{z}_{l, i}\right\|^{2} +∑(l,i)∈Cθ∥(1−μl,i)zl,i−1+μl,izl,i+1−zl,i∥2
第一项:Position-based constraint (apply on source)

第二项:Edge-vector-based constraint (apply on target)

第三项:Smoothness constraint (apply on joint)

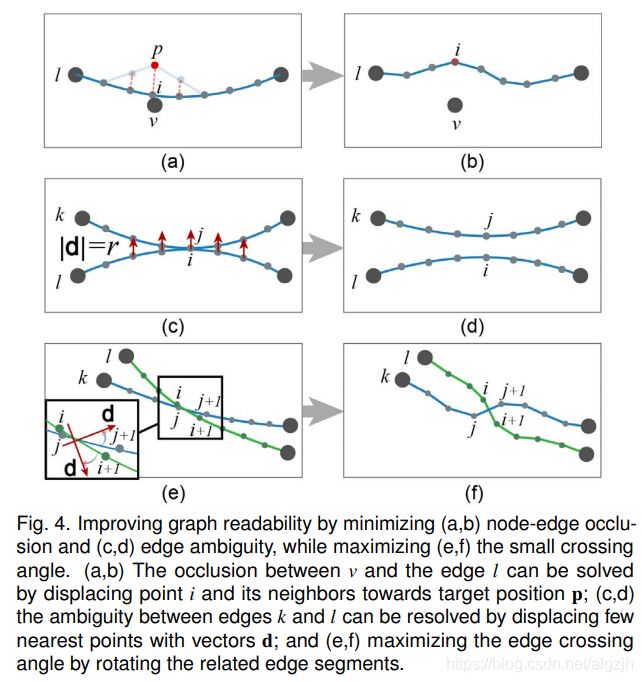
Ambiguity Removal
- Node-edge occlusion
- Edge proximity
- Edge crossing angle
Local Bundling:
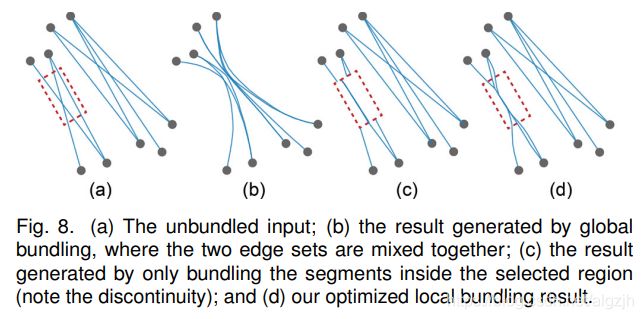
Bundling Interpolation
d l , i l , i + 1 = τ ∗ s d l , i l , i + 1 + ( 1 − τ ) ∗ t d l , i l , i + 1 \mathbf{d}_{l, i}^{l, i+1}=\tau * \mathbf{s d}_{l, i}^{l, i+1}+(1-\tau) * \mathbf{t d}_{l, i}^{l, i+1} dl,il,i+1=τ∗sdl,il,i+1+(1−τ)∗tdl,il,i+1

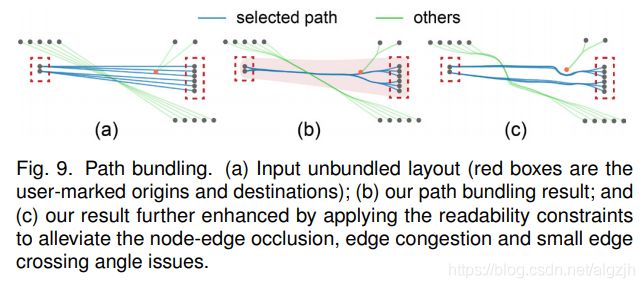
Path Bundling
- Find all the associated paths
- Bundle the selected and background edges separately
- Apply the readability constraint
Density Based Rendering
- Compute a line density map, set the line width according to density
- Compute average local edge density, reorder the edges by this value
- Emphasize the edges by drawing a halo
Application
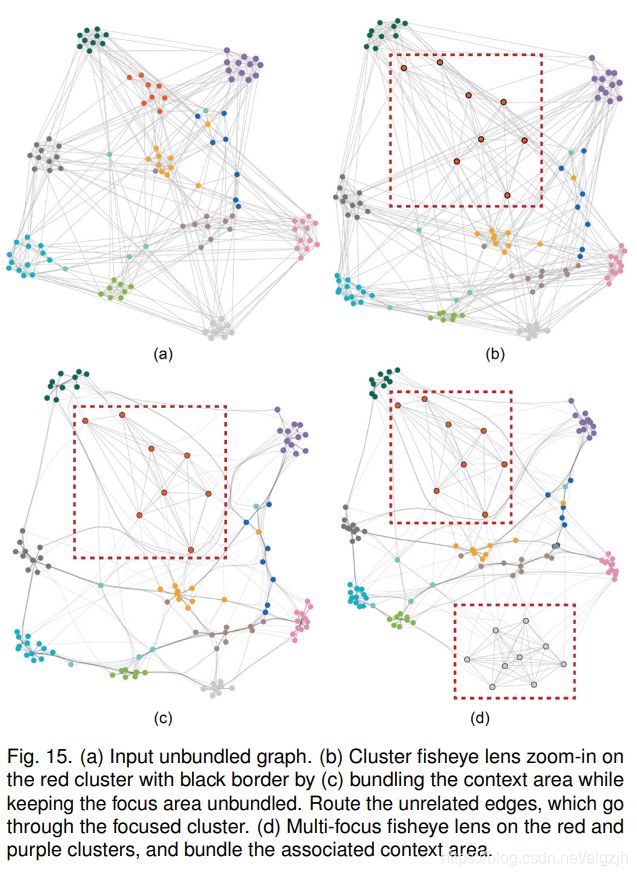
Improving Fisheye Views
Airplane Paths
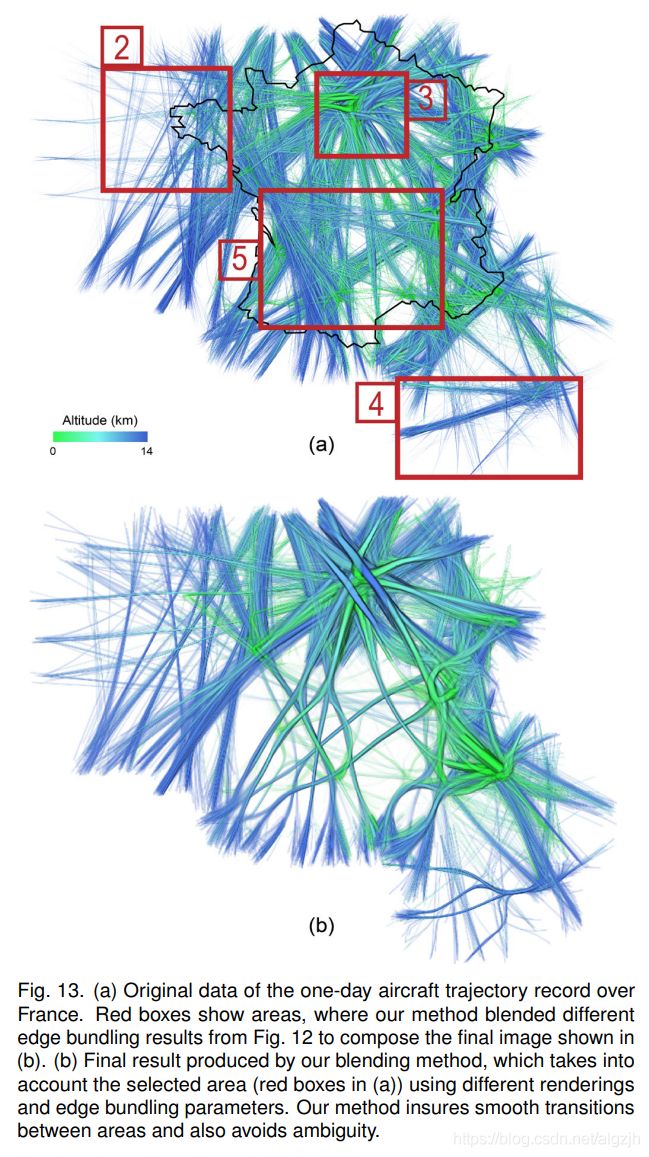
Conclusion
- We propose an optimization framework to flexibly blend edge bundling results and allows to reduce ambiguities when edges overlap with nodes.
- We present several extensions to enable users to further explore the blended edge bundling visualizations.
- We provide an expressive rendering technique that enhances important edges.