求最小生成树,普里姆(Prim)算法
1、 相关概念
1)生成树 一个连通图的生成树是它的极小连通子图,在n个顶点的情形下,有n-1条边。生成树是对连通图而言的,是连同图的极小连通子图,包含图中的所有顶点,有且仅有n-1条边。非连通图的生成树则组成一个生成森林;若图中有n个顶点,m个连通分量,则生成森林中有n-m条边。
2)和树的遍历相似,若从图中某顶点出发访遍图中每个顶点,且每个顶点仅访问一次,此过程称为图的遍历, (Traversing Graph)。图的遍历算法是求解图的连通性问题、拓扑排序和求关键路径等算法的基础。图的遍历顺序有两种:深度优先搜索(DFS)和广度优先搜索(BFS)。对每种搜索顺序,访问各顶点的顺序也不是唯一的。
3)在一个无向连通图G中,其所有顶点和遍历该图经过的所有边所构成的子图G′ 称做图G的生成树。一个图可以有多个生成树,从不同的顶点出发,采用不同的遍历顺序,遍历时所经过的边也就不同。
在图论中,常常将树定义为一个无回路连通图。对于一个带权的无向连通图,其每个生成树所有边上的权值之和可能不同,我们把所有边上权值之和最小的生成树称为图的最小生成树。求图的最小生成树有很多实际应用。例如,通讯线路铺设造价最优问题就是一个最小生成树问题。
常见的求最小生成树的方法有两种:克鲁斯卡尔(Kruskal)算法和普里姆(Prim)算法。
2、 普里姆(Prim)算法
1) 算法的基本思想:
普里姆算法的基本思想:普里姆算法是另一种构造最小生成树的算法,它是按逐个将顶点连通的方式来构造最小生成树的。
从连通网络 N = { V, E }中的某一顶点 u0 出发,选择与它关联的具有最小权值的边(u0, v),将其顶点加入到生成树的顶点集合U中。以后每一步从一个顶点在U中,而另一个顶点不在U中的各条边中选择权值最小的边(u, v),把该边加入到生成树的边集TE中,把它的顶点加入到集合U中。如此重复执行,直到网络中的所有顶点都加入到生成树顶点集合U中为止。
假设G=(V,E)是一个具有n个顶点的带权无向连通图,T(U,TE)是G的最小生成树,其中U是T的顶点集,TE是T的边集,则构造G的最小生成树T的步骤如下:
(1)初始状态,TE为空,U={v0},v0∈V;
(2)在所有u∈U,v∈V-U的边(u,v) ∈E中找一条代价最小的边(u′,v′)并入TE,同时将v′并入U;
重复执行步骤(2)n-1次,直到U=V为止。
在普里姆算法中,为了便于在集合U和(V-U)之间选取权值最小的边,需要设置两个辅助数组closest和lowcost,分别用于存放顶点的序号和边的权值。
对于每一个顶点v∈V-U,closest[v]为U中距离v最近的一个邻接点,即边 (v,closest[v]) 是在所有与顶点v相邻、且其另一顶点j∈U的边中具有最小权值的边,其最小权值为lowcost[v],即lowcost[v]=cost[v][closest[v]],采用邻接表作为存储结构:
设置一个辅助数组closedge[]:
lowcost域 存放生成树顶点集合内顶点到生成树外各顶点的各边上的当前最小权值;
adjvex域 记录生成树顶点集合外各顶点距离集合内哪个顶点最近(即权值最小)。
应用Prim算法构造最小生成树的过程:
如下所示为构造生成树的过程中,辅助数组中各分量值的变化情况,初始归U={v1},加入到U集合中的节点,我们将lowcost改成0以示:
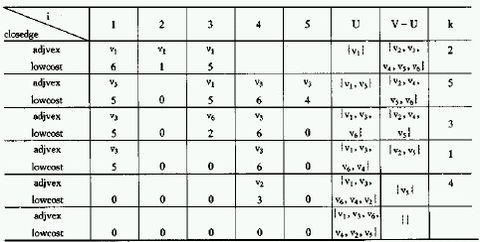
2) 算法的C语言描述:
typedef int VRType;
struct{
VertexType adjvex;
VRType lowcost;
}closedge[MAX_VERTEX_NUM];
void MiniSpanTree_PRIM(MGraph G,VertexType u){
int k,j,i,minCost;
k=LocateVex(G,u);
for (j=0;j
if (j!=k) {
closedge[j].adjvex=u;
closedge[j].lowcost=G.arcs[k][j];
}//初始化
closedge[k].lowcost=0; //将u点加入U集合
for (i=1;i
{ k=minimum(closedge); //求出下一个顶点K
//找k的过程如下
minCost=INFINITY;
for (j=0;j
{
if (closedge[j].lowcost
{ minCost=closedge[j].lowcost; k=j;}
}
//过程如上
printf("(%c,%c)\n",closedge[k].adjvex,G.vexs[k]);
closedge[k].lowcost=0; //加入U集合
for (j=0;j
if (G.arcs[k][j]
{ closedge[j].adjvex=G.vexs[k];//记录刚刚加入U集合的点以备下一轮输出用
closedge[j].lowcost=G.arcs[k][j];
}//if
}
}
普里姆算法中的第二个for循环语句频度为n-1,其中包含的两个内循环频度也都为n-1,因此普里姆算法的时间复杂度为O(n2)。普里姆算法的时间复杂度与边数e无关,该算法更适合于求边数较多的带权无向连通图的最小生成树。
3) 完整实现如下:
#define INFINITY 65535
typedef int status;
# include
# include
# include
# include "string.h"
# define maxlen 10
typedef struct
{
char vexs[maxlen][maxlen];/*顶点信息集合,我们用它来存入顶点名字*/
int vexnum,arcnum;/*顶点数和边数*/
int arcs[maxlen][maxlen];/*邻接矩阵*/
}graph;
//定位输入节点的名称
int LocateVex(graph G,char u[maxlen])
{
int i;
for(i=0;i
if(strcmp(u,G.vexs[i])==0)
return i;
return -1;
}
void prim(graph &g)/*最小生成树*/
{
int i,j,k,min,w,flag;
int lowcost[maxlen];/*权值*/
int closet[maxlen];/*最小生成树结点*/
char va[maxlen],vb[maxlen];
//初始化邻接矩阵
//printf("请输入顶点数和边数:\n");
//scanf("%d%d",&g.vexnum,&g.arcnum);
g.vexnum=6;
g.arcnum=10;
printf("请输入顶点信息(我们这里指名字):\n");
for(int j=0;j
scanf("%s",g.vexs[j]);
for(i=0;i
for(j=0;j
{
g.arcs[i][j]=INFINITY; //任意两个顶点间距离为无穷大。
}//for
/*
printf("请输入%d条弧的弧尾 弧头 权值(以空格为间隔)\n",g.arcnum);
for(k=0;k
{
scanf("%s%s%d%*c",va,vb,&w);//用%*c吃掉回车符
i=LocateVex(g,va); //注意,这里定义的是char va[5],也就是说va是首地址
j=LocateVex(g,vb);
g.arcs[i][j]=w; //无向网
g.arcs[j][i]=w; //无向网
}//for
*/
g.arcs[0][1]=6;
g.arcs[1][0]=6;
g.arcs[0][2]=1;
g.arcs[2][0]=1;
g.arcs[0][3]=5;
g.arcs[3][0]=5;
g.arcs[1][2]=5;
g.arcs[2][1]=5;
g.arcs[1][4]=3;
g.arcs[4][1]=3;
g.arcs[2][3]=5;
g.arcs[3][2]=5;
g.arcs[2][4]=6;
g.arcs[4][2]=6;
g.arcs[2][5]=4;
g.arcs[5][2]=4;
g.arcs[3][5]=2;
g.arcs[5][3]=2;
g.arcs[4][5]=6;
g.arcs[5][4]=6;
printf("最小生成树的边为:\n");
for(i=1;i
{
lowcost[i]=g.arcs[0][i];
closet[i]=1;
}
closet[0]=0; //初始v1是属于集合U的,即设它是最小生成树中节点的一员
j=1; //V是顶点集合
for(i=1;i
{
min=lowcost[j];
k=i;
for(j=1;j
if(lowcost[j]
{
min=lowcost[j];
k=j; //记录当前要加入集合U的节点号
}//if
if(i==1) flag=0;
else flag=closet[k]; //还没有加入集合U的节点的closet[]值是
//记录了上一次加入集合U的节点号
closet[k]=0; //将刚刚找到的点加入到集合U中
printf("(%s,%s),",g.vexs[k],g.vexs[flag]);//输出刚刚找到的最小生成树树枝
for(j=1;j
if(g.arcs[k][j]
{
lowcost[j]=g.arcs[k][j]; //更新lowcost[]的值,且在还没有加入U集合的
//的closet[]中记录刚刚加入U集合的节点号以备
//下一循环中输出用
closet[j]=k;
}
}
}
int main()
{
graph g;
prim(g);
}
