Dijkstra的最小费用最大流问题

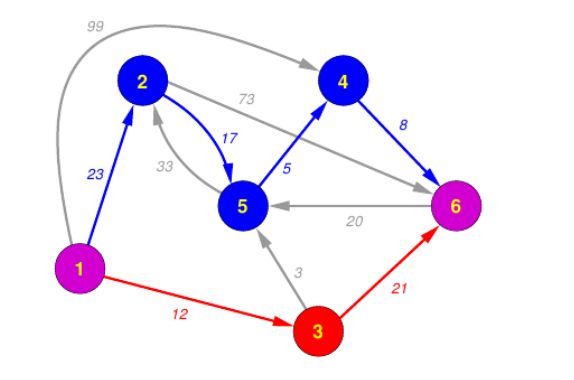
           对于最小费用最大流问题，它的重点就在于   “增广路”    什么是  增广路？ 就是在以找的的路的基础上再加一条路 加上这条路能让结果更大，直接使用 Dijkstra 能找的的路是最短的路，继续用能找到剩下路中间的最小路， 但是这两条路加上来不一定是总体的最小路 ，第一次 1->3 ->5->4->6 第二次1->2->6 这并不是我们需要的结果，所以在找第二条最短路时，我们需要能反悔，能不

让第一次不走3->5，怎么反悔，在构建图时加上一条反边，第一次走了多少正边减少多少反边加上多少，这样第二次就可以走5->3然后走3->6这条线，第一次走了3->5，第二次凑了5->3相当与反悔了第一次的路，这样就能尽可能的走最小路。

#include
#include
#include
using namespace std;
/*6 11 1 2 23 1 3 12 1 4 99 2 5 17 2 6 73 3 5 3 3 6 21 4 6 8 5 2 33 5 4 5 6 5 20*/
#define MAX 23060
int MinCos;
int v,cnt;
int Head[MAX];
int Next[MAX];
int F[MAX];//流量
int To[MAX];//终结的
int Dis[MAX];
int Cos[MAX];//花费
int vis[MAX];
void _add(int a,int b,int f,int c)
{
    cnt++;
    F[cnt]=f;
    To[cnt]=b;
    Cos[cnt]=c;
    Next[cnt]=Head[a];
    Head[a]=cnt;
}
void add(int a,int b,int c)//增加点 用于构图
{
    if(!vis[a]&&a!=1&&a!=v)
    {
        _add(a,a+v,1,0);
        _add(a+v,a,0,0);
        vis[a]=1;
    }
    if(!vis[b]&&b!=1&&b!=v)
    {
        _add(b,b+v,1,0);
        _add(b+v,b,0,0);
        vis[b]=1;
    }
    if(a==1||b==v)
    {
        if(a!=1&&b==v)
        {
            _add(a+v,b,1,c);
            _add(b,a+v,0,-c);
        }else if(a==1&&b!=v)
        {
            _add(a,b,1,c);
            _add(b,a,0,-c);
        }
        else
        {
            _add(a,b,1,c);
            _add(b,a,0,-c);
        }
    }else if(a==v||b==1){}
    else
    {
        _add(a+v,b,1,c);
        _add(b,a+v,0,-c);
    }
}
void Dijks(int folw)//Dijks求最小费用最大流算法
{
    priority_queue,vector >,greater > >sp;
    int h[MAX];
    To[MAX-1]=1;
    memset(h,0,sizeof(h));
    while(folw>0) {
        memset(Dis, 0x3f3f3f3f, sizeof(Dis));
        memset(vis,0,sizeof(vis));
        Dis[1] = 0;
        pair t;
        sp.push(make_pair(0,MAX-1));
        int pre[MAX];
        pre[1] = 0;
        while (!sp.empty()) {
            t = sp.top();
            sp.pop();
            int to = To[t.second];
            if(to==v)continue;
            if(vis[to])continue;
            if (Dis[to] < t.first)continue;//剪枝
            vis[to]=1;
            for (int i = Head[to]; i != -1; i = Next[i]) {
                if (F[i] && Dis[To[i]] > Dis[to] + h[to] - h[To[i]] + Cos[i]) {//跟新最小费用
                    Dis[To[i]] = Dis[to] + h[to] - h[To[i]] + Cos[i];
                    pre[i]=t.second;//记录上一个节点
                    if(To[i]==v)
                    {
                        pre[MAX-2]=i;
                    }
                    sp.push(make_pair(Dis[To[i]], i));
                }
            }
        }
        if(Dis[v]==0x3f3f3f3f)break;
        for (int i = 1; i <= 2*v; i++) {
            h[i] += Dis[i];//我也不是能理解但是有篇博客写的特别好
        }
        for(int i=pre[MAX-2];i!=MAX-1;i=pre[i])//求最小费用
        {
            MinCos+=Cos[i];
            F[i] -= 1;//存入数据时0开始，偶数存正向边，奇数反向边
            F[i ^ 1] += 1;//i^1就是奇数
        }
        folw -= 1;
    }
    cout<>v>>p) {
        for(int i=0;i<20060;i++)
        {
            F[i]=0;
            To[i]=0;
            Dis[i]=0;
            Cos[i]=0;
            vis[i]=0;
            Head[i]=-1;
            Next[i]=-1;
        }
        MinCos=0;
        cnt=-1;
        for (int i = 0; i < p; i++) {
            int a, b, c;
            cin >> a >> b >> c;
            add(a, b, c);
        }
        Dijks(2);
    }
    return 0;
}

 一个大佬讲解h[i]函数的博客http://www.cppblog.com/guojingjia2006/archive/2009/11/12/57905.html

转载于:https://www.cnblogs.com/hycn/p/11329955.html