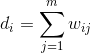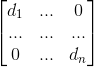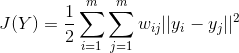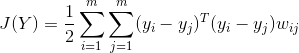流行算法LE_机器学习
前言
拉普拉斯特征映射是基于图论的方法。
它从样本点构造带权值的图W, 然后计算拉普拉斯矩阵
最后对该矩阵进行特征值分解得到投影变换
目录:
- 拉普拉斯矩阵定义
- 目标函数
- 推导过程
- 算法流程
- 算法实现
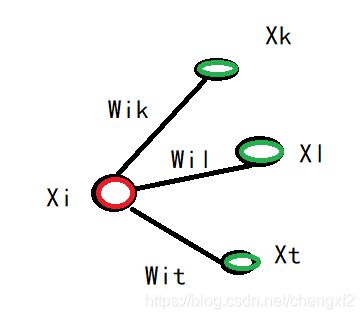
一 拉普拉斯矩阵定义:
![]()
W为低维度权值稀疏矩阵,是一个对称矩阵。每一行代表一个样本点![]()
1.1 邻接关系,可以采用LLE算法里面的k近邻,注意的是LE算法是有向边,这里采用的是无向边
1.2 边的权重,如果节点i和节点j是联通的它们的权重为:
二 目标函数
低维度变量Y为列矩阵
![]()
其中 ![]() 为降维后的样本。
为降维后的样本。
三 推导过程
依然是求最小值
因为W是对称矩阵 ![]()
![]()
![]()
注意: 后半部转换依然要用到W是对称矩阵
约束条件
![]()
拉格朗日对偶求值:
![]()
对Y求偏导数
![]()
依然求解m个最小的非零特征值
四 : 算法流程:
1: 构建无向图
使用某一种方法来将所有的点构建成一个图,例如使用KNN算法,将每个点最近的K个点连上边。
K是一个预先设定的值。
2: 权重W
确定点与点之间的权重大小,例如选用热核函数来确定。
3:特征映射
计算拉普拉斯矩阵L的特征向量与特征值:
Ly=λDy
![]()
4: 用最小的n个非零特征值对应的特征向量作为降维后的结果输出。
五 算法实现
# -*- coding: utf-8 -*-
"""
Created on Mon Oct 14 15:35:00 2019
拉普拉斯降维
@author: chengxf2
"""
from time import time
import matplotlib.pyplot as plt
from mpl_toolkits.mplot3d import Axes3D
from matplotlib.ticker import NullFormatter
from sklearn import manifold, datasets
import pickle
import numpy as np
"""
保存的数据集格式
Args
data: 训练样本
color: 样本点对应的color
"""
class Data:
def __init__(self, data, color):
self.trainData = data
self.dataColor = color
class LE:
"""
·保存文件
Args
file: 文件名
data: 样本
color: 颜色
return
None
"""
def SaveData(self, data ,color):
DataInfo = Data(data,color)
f = open(self.filePath,'wb')
pickle.dump(DataInfo, f,0)
f.close()
"""
初始化
"""
def __init__(self):
self.newDim = 2 ##降维后样本新维度
self.m = 0 ##样本的个数
self.n = 0 ##样本的维度
self.zero = 1e-5 ##当特征值大于该值时,就采用对应的特征向量
self.k = 15 ##k 金陵
self.r = 5.0 ## 半径
self.filePath = "d:\\swissdata.dat" ##数据集路径
"""
从文件中读取数据
Args
file: 文件路劲
return
trainData: 训练样本
color: 样本点对应的color
"""
def LoadFile(self, file):
f = open(file, 'rb')
data = pickle.load(f)
f.close()
trainData = data.trainData
color = data.dataColor
self.Draw(trainData, color,True)
return trainData, color
"""
生成保存流行数据
Args
None
return
None
"""
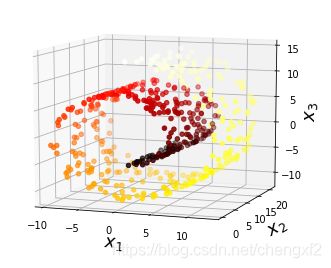
def SWData(self):
n_points = 500
data, color = datasets.samples_generator.make_swiss_roll(n_points, random_state=0)
self.Draw(data, color)
self.SaveData(self.filePath, data,color)
"""
绘制点
Args:
Args
data: 训练样本
color: 样本点对应的color
D3: 画维曲线还是二维曲线
"""
def Draw(self, data, color,D3):
if D3 ==True:
fig = plt.figure(figsize=(6, 5))
ax = fig.add_subplot(111, projection='3d')
ax.scatter(data[:, 0], data[:, 1], data[:, 2], c=color, cmap=plt.cm.hot)
ax.view_init(10, -70)
ax.set_xlabel("$x_1$", fontsize=18)
ax.set_ylabel("$x_2$", fontsize=18)
ax.set_zlabel("$x_3$", fontsize=18)
else:
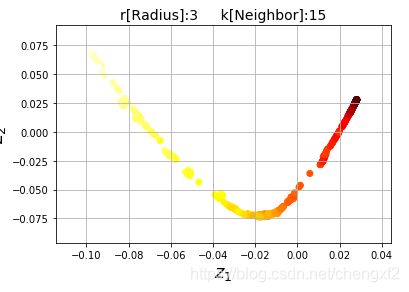
Tip ="r[Radius]:%d"%self.r + " k[Neighbor]:%d"%self.k
print("Tip ",Tip)
plt.title(Tip, fontsize=14)
plt.scatter(data[:, 0], data[:, 1], c=color, cmap=plt.cm.hot)
plt.xlabel("$z_1$", fontsize=18)
plt.ylabel("$z_2$", fontsize=18)
plt.grid(True)
plt.show()
"""
获取权重参数
Args
xi 当前样本
xj: 临近样本
t: 半径
"""
def Getw(self, xi,xj):
diff = (xi-xj)**2
dist = diff.sum( axis=0) ##行
alpha = np.exp(-dist/self.r)
return alpha
"""
拉普拉降维Laplar dimensionality reduction
Args
k: k 个近邻
t: exp 中分母
dataMat: 数据集
"""
def Ldr(self, trainData):
wMat = np.zeros((self.m,self.m))
DMat= np.zeros((self.m,self.m))
print("\n step1 计算临近样本的权重 \n")
for i in range(self.m):
xi = trainData[i]
sortK = self.GetKNear(xi, trainData,i) ##返回临近的Index
for j in sortK:
xj = trainData[j]
alpha = self.Getw(xi, xj)
wMat[i,j]=alpha
wMat[j,i] = wMat[i,j]
di=sum(wMat[i,])
DMat[i,i]=di
print("\n step2 拉普拉斯矩阵计算 \n")
L = DMat-wMat
invD = np.linalg.inv(DMat)
LD = np.dot(invD,L)
print("\n step3 计算特征值特征向量")
lamb, Y = np.linalg.eig(LD)
print("\n step3 排序特征值")
sortIndex = lamb.argsort()
#print("lamb ",lamb)
#print("sortIndex: ",sortIndex)
num = 0
indexList =[]
for index in sortIndex:
lam = lamb[index]
if lam>self.zero and num
效果:
说明:
相对LLE算法
1: LE权重是对称矩阵
2: 模型对k,以及r的取值很敏感(r 上文中的t值),总的来说效果不错。
参考文档:
《机器学习与应用》 119页