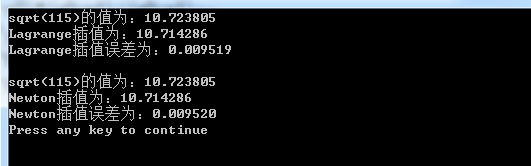
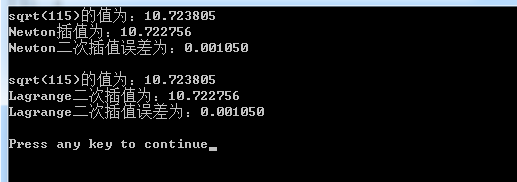
用Sqrt函数计算根号下115的值（近似认为准确值），分别给出两个误差值，分析产生误差的原因。

（1）在x=100,121两点处误差为：

#include

#include

int main()

{

    int x=115,x0=100,x1=121;

    double y,y0,y1,f,h;

    float l0,l1;

    y=sqrt(x);

    y0=sqrt(x0);

    y1=sqrt(x1);

 

    l0=(float)(x-x1)/(x0-x1);

    l1=(float)(x-x0)/(x1-x0);

    f=y0*l0+y1*l1;

    printf("sqrt(115)的值为：%f\n",y);

    printf("Lagrange插值为：%f\n",f);

    printf("Lagrange插值误差为：%f\n\n",y-f);

 

    h=y0+(x-x0)*((y0-y1)/(x0-x1));

    printf("sqrt(115)的值为：%f\n",y);

    printf("Newton插值为：%f\n",h);

    printf("Newton插值误差为：%f\n",y-h);

}

（2）在x=100,121,144三点处的误差为：

#include

#include

int main()

{

    int x=115,x0=100,x1=121,x2=144;

    double y,y0,y1,y2,h,h1;

    float f1,f2,f3,l0,l1,l2;

    y=sqrt(x);

    y0=sqrt(x0);

    y1=sqrt(x1);

    y2=sqrt(x2);

    f1=(float)(y0-y1)/(x0-x1);

    f2=(float)(y1-y2)/(x1-x2);

    f3=(f1-f2)/(x0-x2);

    h=y0+(x-x0)*f1+(x-x0)*(x-x1)*f3;

    printf("sqrt(115)的值为：%f\n",y);

    printf("Newton插值为：%f\n",h);

    printf("Newton二次插值误差为：%f\n\n",y-h);

 

    l0=(float)(x-x1)*(x-x2)/((x0-x1)*(x0-x2));

    l1=(float)(x-x0)*(x-x2)/((x1-x0)*(x1-x2));

    l2=(float)(x-x0)*(x-x1)/((x2-x0)*(x2-x1));

    h1=y0*l0+y1*l1+y2*l2;

    printf("sqrt(115)的值为：%f\n",y);

    printf("Lagrange二次插值为：%f\n",h);

    printf("Lagrange二次插值误差为：%f\n\n",y-h);

}

Lagrange插值是对若干个多项式的线性组合，Newton插值是由各阶均差组合得到的。在计算的过程中发现Lagrange的插值多项式和Newton的插值多项式相比，Lagrange的插值多项式的计算量比较大，并且当增加一个插值结点的时候，Newton插值需要新增需要的均差，而Lagrange插值需要重新计算基函数；在实验中，由于计算机进行运算的时候，产生了截断误差，所以计算得到的结果相对来说不是很精确。