线性回归——最小二乘法代数详细计算过程

Reference: 动手实战人工智能 AI By Doing
关于矩阵方法的求解可参考：最小二乘法矩阵详细计算过程

基本定义：

通过找到一条直线去拟合数据点的分布趋势的过程，就是线性回归的过程。

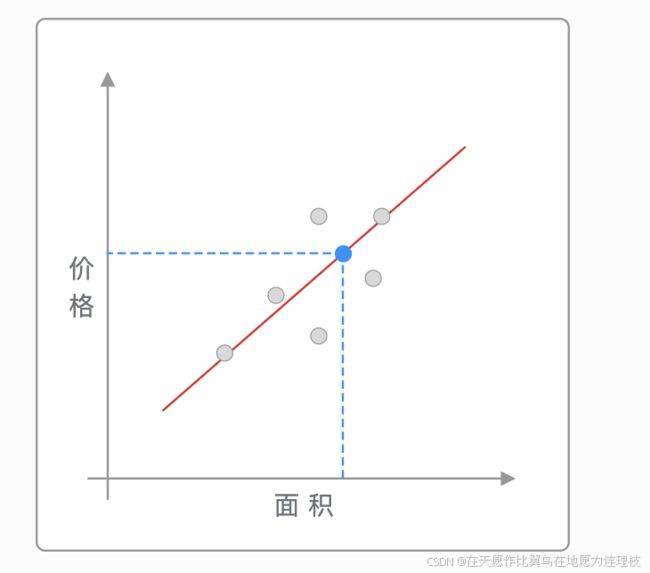
在上图呈现的这个过程中，通过找到一条直线去拟合数据点的分布趋势的过程，就是线性回归的过程。而线性回归中的「线性」代指线性关系，也就是图中所绘制的红色直线。
所以，找到最适合的那一条红色直线，就成为了线性回归中需要解决的目标问题。

一元线性回归

令该一次函数表达式为 $y(x,w)=w_0+w_{1}x$ 通过组合不同的 $w_0$ 和 $w_1$ 的值得到不同的拟合直线

def f(x: list, w0: float, w1: float):
    """一元一次函数表达式"""
    y = w0 + w1 * x
    return y

平方损失函数

• 如果一个数据点为 ($x_i$, $y_i$)，那么它对应的误差（残差）就为：$y_i-(w_0+w_{1}x)$
• 那么，对$n$个全部数据点而言，其对应的残差损失总和就为：
  $$\sum _{i=1}^n(y_i-(w_0+w_1{x}_i))$$
• 我们一般使用残差的平方和来表示所有样本点的误差。公式如下：
  $$\sum _{i=1}^n(y_i-(w_0+w_1{x}_i){)}^2$$
  好处：在于能保证损失始终是累加的正数，而不会存在正负残差抵消的问题

def square_loss(x: np.ndarray, y: np.ndarray, w0: float, w1: float):
    """平方损失函数"""
    loss = sum(np.square(y - (w0 + w1 * x)))
    return loss

求解损失最小值的过程，就必须用到下面的数学方法：

最小二乘法代数求解

「二乘」代表平方，「平方」指的是上文的平方损失函数，最小二乘法也就是求解平方损失函数最小值的方法
$$f=\sum _{i=1}^n(y_i-(w_0+w_1{x}_i){)}^2$$
$$\frac{\partial f}{\partial w_0}=-2(\sum _{i=1}^n{y}_i-n{w}_0-w_1\sum _{i=1}^n{x}_i)$$
$$\frac{\partial f}{\partial w_1}=-2(\sum _{i=1}^n{x}_i{y}_i-w_0\sum _{i=1}^n{x}_i-w_1\sum _{i=1}^n{x}_i^2)$$
令$\frac{\partial f}{\partial w_0}=0$和$\frac{\partial f}{\partial w_1}=0$得：
$$w_1=\frac{n\sum x_i{y}_i-\sum x_i\sum y_i}{n\sum x_i^2-(\sum x_i{)}^2}$$
$$w_0=\frac{\sum x_i^2\sum y_i-\sum x_i\sum x_i{y}_i}{n\sum x_i^2-(\sum x_i{)}^2}$$

def least_squares_algebraic(x: np.ndarray, y: np.ndarray):
    """最小二乘法代数求解"""
    n = x.shape[0]
    w1 = (n * sum(x * y) - sum(x) * sum(y)) / (n * sum(x * x) - sum(x) * sum(x))
    w0 = (sum(x * x) * sum(y) - sum(x) * sum(x * y)) / (
        n * sum(x * x) - sum(x) * sum(x)
    )
    return w0, w1
"""绘图"""
w0 = least_squares_algebraic(x, y)[0]
w1 = least_squares_algebraic(x, y)[1]
plt.scatter(x, y)
plt.plot(x_temp, x_temp * w1 + w0, "r")

详细计算过程

对$w_0$求偏导
$$\begin{array}{rl}\frac{\partial }{\partial w_0}\sum _{i=1}^n(y_i-(w_0+w_1{x}_i){)}^2& =\sum _{i=1}^n\frac{\partial (u_i^2)}{\partial w_0}\\ & =\sum _{i=1}^n-2(y_i-(w_0+w_1{x}_i))\\ & =-2\sum _{i=1}^n(y_i-(w_0+w_1{x}_i))\end{array}$$
对$w_1$求偏导
$$\begin{array}{rl}\frac{\partial }{\partial w_1}\sum _{i=1}^n(y_i-(w_0+w_1{x}_i){)}^2& =\sum _{i=1}^n\frac{\partial (u_i^2)}{\partial w_1}\\ & =\sum _{i=1}^n-2x_i(y_i-(w_0+w_1{x}_i))\\ & =-2\sum _{i=1}^n{x}_i(y_i-(w_0+w_1{x}_i))\end{array}$$
令$\frac{\partial f}{\partial w_0}=0$和$\frac{\partial f}{\partial w_1}=0$得：
$$w_0=\frac{1}{n}\left(\sum _{i=1}^n{y}_i-w_1\sum _{i=1}^n{x}_i\right)$$
$$\sum _{i=1}^n{x}_i{y}_i-w_0\sum _{i=1}^n{x}_i-w_1\sum _{i=1}^n{x}_i^2=0$$
将$(w_0=\frac{1}{n}\left({\sum }_{i=1}^n{y}_i-w_1{\sum }_{i=1}^n{x}_i\right)$代入$({\sum }_{i=1}^n{x}_i{y}_i-w_0{\sum }_{i=1}^n{x}_i-w_1{\sum }_{i=1}^n{x}_i^2=0)$中：
∑ i = 1 n x i y i − 1 n ( ∑ i = 1 n y i − w 1 ∑ i = 1 n x i ) ∑ i = 1 n x i − w 1 ∑ i = 1 n x i 2 = 0 n ∑ i = 1 n x i y i − ( ∑ i = 1 n y i − w 1 ∑ i = 1 n x i ) ∑ i = 1 n x i − n w 1 ∑ i = 1 n x i 2 = 0 n ∑ i = 1 n x i y i − ∑ i = 1 n x i ∑ i = 1 n y i + w 1 ( ∑ i = 1 n x i ) 2 − n w 1 ∑ i = 1 n x i 2 = 0 w 1 ( n ∑ i = 1 n x i 2 − ( ∑ i = 1 n x i ) 2 ) = n ∑ i = 1 n x i y i − ∑ i = 1 n x i ∑ i = 1 n y i w 1 = n ∑ i = 1 n x i y i − ∑ i = 1 n x i ∑ i = 1 n y i n ∑ i = 1 n x i 2 − ( ∑ i = 1 n x i ) 2 \begin{align*} \sum_{i = 1}^{n}x_iy_i-\frac{1}{n}\left(\sum_{i = 1}^{n}y_i - w_1\sum_{i = 1}^{n}x_i\right)\sum_{i = 1}^{n}x_i - w_1\sum_{i = 1}^{n}x_i^2&=0\\ n\sum_{i = 1}^{n}x_iy_i-\left(\sum_{i = 1}^{n}y_i - w_1\sum_{i = 1}^{n}x_i\right)\sum_{i = 1}^{n}x_i - n w_1\sum_{i = 1}^{n}x_i^2&=0\\ n\sum_{i = 1}^{n}x_iy_i-\sum_{i = 1}^{n}x_i\sum_{i = 1}^{n}y_i + w_1\left(\sum_{i = 1}^{n}x_i\right)^2- n w_1\sum_{i = 1}^{n}x_i^2&=0\\ w_1\left(n\sum_{i = 1}^{n}x_i^2-\left(\sum_{i = 1}^{n}x_i\right)^2\right)&=n\sum_{i = 1}^{n}x_iy_i-\sum_{i = 1}^{n}x_i\sum_{i = 1}^{n}y_i\\ w_1&=\frac{n\sum_{i = 1}^{n}x_iy_i-\sum_{i = 1}^{n}x_i\sum_{i = 1}^{n}y_i}{n\sum_{i = 1}^{n}x_i^2-\left(\sum_{i = 1}^{n}x_i\right)^2} \end{align*} i=1∑n​xi​yi​−n1​(i=1∑n​yi​−w1​i=1∑n​xi​)i=1∑n​xi​−w1​i=1∑n​xi2​ni=1∑n​xi​yi​−(i=1∑n​yi​−w1​i=1∑n​xi​)i=1∑n​xi​−nw1​i=1∑n​xi2​ni=1∑n​xi​yi​−i=1∑n​xi​i=1∑n​yi​+w1​(i=1∑n​xi​)2−nw1​i=1∑n​xi2​w1​ ​ni=1∑n​xi2​−(i=1∑n​xi​)2 ​w1​​=0=0=0=ni=1∑n​xi​yi​−i=1∑n​xi​i=1∑n​yi​=n∑i=1n​xi2​−(∑i=1n​xi​)2n∑i=1n​xi​yi​−∑i=1n​xi​∑i=1n​yi​​​
$$\begin{array}{rl}{w}_0& =\frac{1}{n}\left[\sum _{i=1}^n{y}_i-\frac{n{\sum }_{i=1}^n{x}_i{y}_i-{\sum }_{i=1}^n{x}_i{\sum }_{i=1}^n{y}_i}{n{\sum }_{i=1}^n{x}_i^2-({\sum }_{i=1}^n{x}_i{)}^2}\cdot \sum _{i=1}^n{x}_i\right]\\ & =\frac{1}{n}\cdot \frac{(n{\sum }_{i=1}^n{x}_i^2-({\sum }_{i=1}^n{x}_i{)}^2){\sum }_{i=1}^n{y}_i-(n{\sum }_{i=1}^n{x}_i{y}_i-{\sum }_{i=1}^n{x}_i{\sum }_{i=1}^n{y}_i){\sum }_{i=1}^n{x}_i}{n{\sum }_{i=1}^n{x}_i^2-({\sum }_{i=1}^n{x}_i{)}^2}\\ & =\frac{(n{\sum }_{i=1}^n{x}_i^2-({\sum }_{i=1}^n{x}_i{)}^2){\sum }_{i=1}^n{y}_i-n{\sum }_{i=1}^n{x}_i{y}_i{\sum }_{i=1}^n{x}_i+{\sum }_{i=1}^n{x}_i{\sum }_{i=1}^n{y}_i{\sum }_{i=1}^n{x}_i}{n(n{\sum }_{i=1}^n{x}_i^2-({\sum }_{i=1}^n{x}_i{)}^2)}\\ & =\frac{n{\sum }_{i=1}^n{x}_i^2{\sum }_{i=1}^n{y}_i-({\sum }_{i=1}^n{x}_i{)}^2{\sum }_{i=1}^n{y}_i-n{\sum }_{i=1}^n{x}_i{y}_i{\sum }_{i=1}^n{x}_i+{\left({\sum }_{i=1}^n{x}_i\right)}^2{\sum }_{i=1}^n{y}_i}{n(n{\sum }_{i=1}^n{x}_i^2-({\sum }_{i=1}^n{x}_i{)}^2)}\\ & =\frac{n{\sum }_{i=1}^n{x}_i^2{\sum }_{i=1}^n{y}_i-n{\sum }_{i=1}^n{x}_i{y}_i{\sum }_{i=1}^n{x}_i}{n(n{\sum }_{i=1}^n{x}_i^2-({\sum }_{i=1}^n{x}_i{)}^2)}\\ & =\frac{{\sum }_{i=1}^n{x}_i^2{\sum }_{i=1}^n{y}_i-{\sum }_{i=1}^n{x}_i{\sum }_{i=1}^n{x}_i{y}_i}{n{\sum }_{i=1}^n{x}_i^2-({\sum }_{i=1}^n{x}_i{)}^2}\end{array}$$
因此：
$$w_1=\frac{n\sum x_i{y}_i-\sum x_i\sum y_i}{n\sum x_i^2-(\sum x_i{)}^2}$$
$$w_0=\frac{\sum x_i^2\sum y_i-\sum x_i\sum x_i{y}_i}{n\sum x_i^2-(\sum x_i{)}^2}$$