矩阵乘法的一些应用

矩阵

在数学中，矩阵（matrix）是一个按照长方阵列排列的复数或实数集合 ，最早来自于方程组的系数及常数所构成的方阵。
为什么用矩阵？
矩阵把分散的数据集中到了一起，在各方面上（数学、物理学等）都有应用
（声明：接下来的图大部分copy from百度……）

---

定义很重要

由 m×n m × n 个数 aij a i j 排成的m行n列的数表称为 m m 行 n n 列的矩阵，简称 m×n m × n 矩阵。记作：

这 m×n m × n 个数称为矩阵 A A 的元素，简称为元，数 aij a i j 位于矩阵 A A 的第 i i 行第 j j 列，称为矩阵 A A 的 (i,j) ( i , j ) 元

元素是实数的矩阵称为实矩阵，元素是复数的矩阵称为复矩阵
行数与列数都 =n = n 的矩阵称为 n n 阶矩阵或 n n 阶方阵
（说白了，就是个二维数组）

---

矩阵的计算

线性运算

---

矩阵加

（只有同型矩阵才可以加）

矩阵加满足交换律和结合律，即：

A+B=B+A A + B = B + A

(A+B)+C=A+(B+C) ( A + B ) + C = A + ( B + C )

---

矩阵减

（也是只有同型矩阵才可以减）

---

数乘矩阵

数乘矩阵满足（ λ,μ λ , μ 为数， A,B A , B 为矩阵）

(λμ)A=λ(μA) ( λ μ ) A = λ ( μ A )

(λ+μ)A=λA+μA ( λ + μ ) A = λ A + μ A

λ(A+B)=λA+λB λ ( A + B ) = λ A + λ B

矩阵加减和数乘矩阵合称矩阵的线性运算

---

其他操作&计算

转置

把矩阵A的行和列互相交换所产生的矩阵称为A的转置矩阵，这一过程称为矩阵的转置

转置满足

(AT)T=A ( A T ) T = A

(λA)T=λAT ( λ A ) T = λ A T

(AB)T=BTAT ( A B ) T = B T A T

---

共轭

矩阵的共轭定义为

的共轭矩阵为

复数不是表示成 a+bi a + b i 的形式吗（ a a 是实部， b b 是虚部， i i 是虚数单位）
说白了，共轭就是把矩阵里的每一个复数的虚部b取反而已，高中不是会学的吗┑(￣Д ￣)┍

---

共轭转置

共轭转置就是先转置矩阵再共轭一次
矩阵的共轭转置定义为：，也可以写为：

如果有那么 A A 的共轭转置矩阵为

---

普通的矩阵操作讲完了
上面的东西是不是十wu分~~ru~~简zhi单~~shang~~？
下面这个东东才是要讲的重点

---

矩阵乘法

（矩阵相乘只有在第一个矩阵的列数和第二个矩阵的行数相同时才有意义 ）

设矩阵 A A 为 m×p m × p 的矩阵，矩阵 B B 为 p×n p × n 的矩阵，那么 A×B A × B 的积 C C 是个 m×n m × n 的矩阵，记 C=AB C = A B
其中 C C 的第 i i 行第 j j 列为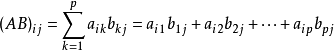

更容易看一点的

矩阵相乘满足

(AB)C=A(BC) ( A B ) C = A ( B C )

(A+B)C=AC+BC ( A + B ) C = A C + B C

C(A+B)=CA+CB C ( A + B ) = C A + C B

k(AB)=(kA)B=A(kB) k ( A B ) = ( k A ) B = A ( k B )

(AB)T=BTAT ( A B ) T = B T A T

一定要引起注意的是，矩阵乘法一般不满足乘法交换律！
为什么不满足交换律？
设 A A 为 2×3 2 × 3 的矩阵， B B 为 3×5 3 × 5 的矩阵，你试试B·A乘的起来吗……呵呵

先把上面的定义看懂，再讨论我们接下来的矩阵乘法吧

---

例题

---

例题1：斐波那契数列

problem

补充：f[0]=0，f[1]=1，n≤10^18

---

斐波那契数列是一道非常非常基础的题目了，用普通的递推可以解决
但是 n n 有 1018 10 18 ，我们不可能用递推来做这道题

为了更高效地解决这道题，我们就必须用矩阵乘法了
使用矩阵乘法，我们需要数学建模，构造矩阵式
（构造矩阵式是解决矩阵乘法类的题目最重要的步骤，例如DP推状态一样）

---

构造矩阵式

现在，我们有 A=(f[x−1],f[x−2]) A = ( f [ x − 1 ] , f [ x − 2 ] ) ， B=(f[x],f[x−1]) B = ( f [ x ] , f [ x − 1 ] )
我们就构造一个矩阵 T T 使得

A×T=B A × T = B

如何构造？

• f[x−1] f [ x − 1 ] 对 f[x] f [ x ] 的贡献为 f[x−1]∗1 f [ x − 1 ] ∗ 1 ，所以 T1,1=1 T 1 , 1 = 1
• f[x−2] f [ x − 2 ] 对 f[x−1] f [ x − 1 ] 的贡献为 f[x−2]∗1 f [ x − 2 ] ∗ 1 ，所以 T1,2=1 T 1 , 2 = 1
• f[x−1] f [ x − 1 ] 对 f[x−1] f [ x − 1 ] 的贡献为 f[x−1]∗1 f [ x − 1 ] ∗ 1 ，所以 T2,1=1 T 2 , 1 = 1
• f[x−2] f [ x − 2 ] 对 f[x−1] f [ x − 1 ] 的贡献为 f[x−2]∗0 f [ x − 2 ] ∗ 0 ，所以 T2,2=0 T 2 , 2 = 0

这个矩阵就是—— (1,11,0) ( 1 , 1 1 , 0 )

那么斐波那契数列的另一种通项公式我们就可以轻松地写出来了——

(f[n−1],f[n−2])×(1,11,0)=(f[n],f[n−1]) ( f [ n − 1 ] , f [ n − 2 ] ) × ( 1 , 1 1 , 0 ) = ( f [ n ] , f [ n − 1 ] )

so——

(f[1],f[0])×(1,11,0)n−1=(f[n],f[n−1]) ( f [ 1 ] , f [ 0 ] ) × ( 1 , 1 1 , 0 ) n − 1 = ( f [ n ] , f [ n − 1 ] )

明显地，我们只需求出中间那个矩阵的 n−1 n − 1 次方即可，怎么求？
我们不可能像定义一样去求它的 n−1 n − 1 次方，时间绝对会爆炸

其实非常简单，因为矩阵自己乘自己和快速幂是一模一样的，时间复杂度 O(n3log2k) O ( n 3 l o g 2 k )

---

矩阵快速幂code

matrix I=  
{  
    1,0,  
    0,1  
}; //这里的I是矩阵意义上的1,因为(x,y)*I=(x,y)

matrix power(matrix a,long long k)  
{  
    matrix ans=I,p=a;
    while(k)  
    {  
        if(k&1)ans=ans*p;  //这个*需要重载符号
        p=p*p;  
        k/=2;  
    }  
    return ans;  
}  

怎么样？是不是和快速幂如出一辙？

如何重载*符号？
就按照矩阵乘法的定义重载就行了，时间复杂度 O(n3) O ( n 3 )

---

矩阵乘法code

matrix operator*(matrix a,matrix b)  
{  
    matrix c;  
    for(int i=0;i<=1;i++)  
    { 
        for(int j=0;j<=1;j++)  
        {  
            c.m[i][j]=0;  
            for(int k=0;k<=1;k++)
            {
                (c.m[i][j]+=a.m[i][k]*b.m[k][j]%MAXN)%=MAXN;
            }
        }  
    }  
    return c;  
}  

---

so把两个东东结合到一起，就可以快速求斐波那契数列第 n n 项了

code

#include     

using namespace std;

long long n,MAXN;

struct matrix  
{  
    long long m[2][2];  
};  

matrix A=  
{  
    1,1,  
    1,0  
};  

matrix I=  
{  
    1,0,  
    0,1  
};  

matrix operator*(matrix a,matrix b)  
{  
    matrix c;  
    for(int i=0;i<=1;i++)  
    { 
        for(int j=0;j<=1;j++)  
        {  
            c.m[i][j]=0;  
            for(int k=0;k<=1;k++)
            {
                (c.m[i][j]+=a.m[i][k]*b.m[k][j]%MAXN)%=MAXN;
            }
        }  
    }  
    return c;  
}  

matrix power(matrix a,long long k)  
{  
    matrix ans=I,p=a;  
    while(k)  
    {  
        if(k&1)ans=ans*p;  
        p=p*p;  
        k/=2;  
    }  
    return ans;  
}  

int main()  
{  
    scanf("%lld%lld",&n,&MAXN);
    matrix ans=power(A,n-1);  
    printf("%lld\n",ans.m[0][0]);
    return 0;  
}  

并没有想象中的困难？
斐波那契数列可以很好地帮助我们快速上手矩阵乘法，收获还是比较大的
下面是另一道斐波那契数列题目

---

例题2：JZOJsenior1240.Fibonacci sequence

problem

---

analysis

• 正解矩阵乘法

• 斐波那契数列的第几项，非常好求

• 但是斐波那契数列有求和公式么？能用矩乘求么？

• a1=a2=1,ak=ak−1+ak−2(k∈[3,∞),k∈N) a 1 = a 2 = 1 , a k = a k − 1 + a k − 2 ( k ∈ [ 3 , ∞ ) , k ∈ N )

• 设Sn=∑i=1nai 设 S n = ∑ i = 1 n a i

• Sn=a1+a2+a3+...an=1+a1+a2+a3...+an−1 S n = a 1 + a 2 + a 3 + . . . a n = 1 + a 1 + a 2 + a 3 . . . + a n − 1

• ∵a2=1,∴Sn=a2+a1+a2+a3+...+an−1 ∵ a 2 = 1 , ∴ S n = a 2 + a 1 + a 2 + a 3 + . . . + a n − 1

• ∵a2+a1=a3,∴Sn=a3+a2+a3+...+an−1 ∵ a 2 + a 1 = a 3 , ∴ S n = a 3 + a 2 + a 3 + . . . + a n − 1

• ∴Sn=an+1+an−1=an+2−1 ∴ S n = a n + 1 + a n − 1 = a n + 2 − 1

• 所以直接矩阵快速幂即可， ans a n s 即为 ay+2−ax+2 a y + 2 − a x + 2

---

code

#include 
#define mod 10000ll

using namespace std;

long long n;
int t;

struct matrix  
{  
    long long m[2][2];  
};  

matrix A=  
{  
    1,1,  
    1,0  
};  

matrix I=  
{  
    1,0,  
    0,1  
};  

matrix operator*(matrix a,matrix b)  
{  
    matrix c;  
    for(int i=0;i<=1;i++)  
    { 
        for(int j=0;j<=1;j++)  
        {  
            c.m[i][j]=0;  
            for(int k=0;k<=1;k++)
            {
                (c.m[i][j]+=a.m[i][k]*b.m[k][j]%mod)%=mod;
            }
        }  
    }  
    return c;  
}  

matrix power(matrix a,long long k)  
{  
    matrix ans=I,p=a;  
    while(k)  
    {  
        if(k&1)ans=ans*p;  
        p=p*p;  
        k/=2;  
    }  
    return ans;  
}  

int main()  
{  
    scanf("%d",&t);
    while (t--)
    {
        long long x,y;
        scanf("%lld%lld",&x,&y);    
        printf("%lld\n",(power(A,y+1).m[0][0]-power(A,x).m[0][0]+mod)%mod);
    }
    return 0;  
}

---

例题3：【NOI2012】随机数生成器

problem

Description

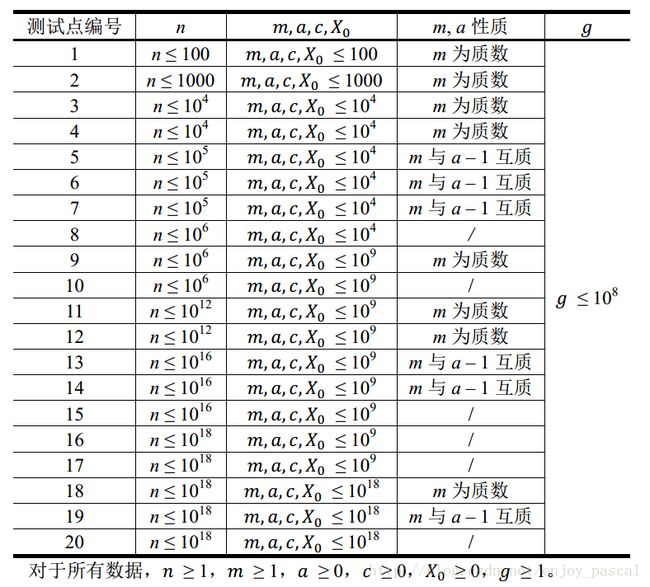
栋栋最近迷上了随机算法，而随机数生成是随机算法的基础。栋栋准备使用线性同余法（Linear Congruential
Method）来生成一个随机数列，这种方法需要设置四个非负整数参数 m, a, c, X0，按照下面的公式生成出一系列随机数：

Xn+1=(aXn+c) mod m

其中 mod m 表示前面的数除以m的余数。从这个式子可以看出，这个序列的下一个数总是由上一个数生成的。

用这种方法生成的序列具有随机序列的性质，因此这种方法被广泛地使用，包括常用的 C++和 Pascal
的产生随机数的库函数使用的也是这种方法。

栋栋知道这样产生的序列具有良好的随机性，不过心急的他仍然想尽快知道Xn是多少。由于栋栋需要的随机数是0, 1, … ,n−1
之间的，他需要将 Xn 除以g取余得到他想要的数，即 Xn mod g，你只需要告诉栋栋他想要的数Xn mod g是多少就可以了。

Input

输入中包含 6 个用空格分割的整数m, a, c, X0, n和g，其中a, c, X0是非负整数，m, n, g是正整数。

Output

输出一个数，即Xn mod g

Sample Input

11 8 7 1 5 3

Sample Output

2

Data Constraint

Hint

Xn的前几项依次是:

k 0 1 2 3 4 5

Xk 1 4 6 0 7 8

因此答案为X5 mod g = 8 mod 3 = 2

---

这题虽说O（n）的暴力也能拿到50分，但在考场上有多少OIers会满足于区区50分呢？
正解：矩阵乘法get√

---

构造矩阵式

首先我们可以很明显地推出一个东西：

(An)×(ac)=(a⋅An+c) ( A n ) × ( a c ) = ( a · A n + c )

明显地，这个矩阵式对解题没有任何意义，why？
既然是矩阵的幂，那么中间那个转移矩阵必须是n×n的，否则乘不起来

那么，从初始矩阵出发，我们尝试把转移矩阵变成n×n的：

把 (An) ( A n ) 写成 (An,p) ( A n , p ) ，那么——

(An,p)×(a,0c,1)=(a⋅An+c,p) ( A n , p ) × ( a , 0 c , 1 ) = ( a · A n + c , p )

（注意，这步是 十分灵活的，给原矩阵添一些 无用的元素可能是解决问题的 关键）
所以——

(A0,p)×(a,0c,1)n=(An,p) ( A 0 , p ) × ( a , 0 c , 1 ) n = ( A n , p )

（反正我取的p是1，其实p取什么值都无所谓）

---

所以，这道题就变得十分简单啦，直接套矩乘模板快速幂，then AC

（另，你想想两个10^18的long long乘起来会不会炸掉？
答案是肯定的，WA85，解决方法是把所有long long的相乘换成快速乘即可
快速乘姿势）

---

快速乘code

long long mul(long long x,long long y)
{
    long long ans=0;
    while (y)
    {
        if (y&1)ans=(ans+x)%m;
        x=2*x%m;
        y/=2;
    }
    return ans;
}

其实快速乘和快速幂没什么区别……变了两个字母而已（但它不会爆long long就对了）

code

#include

using namespace std;

long long m,a,c,x0,n,g;

struct matrix
{
    long long m[2][2];
};

matrix I=
{
    1,0,
    0,1
};

long long mul(long long x,long long y)
{
    long long ans=0;
    while (y)
    {
        if (y&1)ans=(ans+x)%m;
        x=2*x%m;
        y/=2;
    }
    return ans;
}

matrix operator *(matrix a,matrix b)
{
    matrix c;
    for (int i=0;i<=1;i++)
    {
        for (int j=0;j<=1;j++)
        {
            c.m[i][j]=0;
            for (int k=0;k<=1;k++)(c.m[i][j]+=mul(a.m[i][k],b.m[k][j]))%=m;
        }
    }
    return c;
}

matrix power(matrix a,long long k)
{
    matrix ans=I,p=a;
    while (k)
    {
        if (k&1)ans=ans*p;
        p=p*p;
        k/=2;
    }
    return ans;
}


int main()
{
    scanf("%lld%lld%lld%lld%lld%lld",&m,&a,&c,&x0,&n,&g);
    matrix A=
    {
        a,0,
        c,1
    };
    matrix answer=power(A,n);
    long long k=(mul(x0,answer.m[0][0])+answer.m[1][0])%m;
    printf("%lld",k%g);
    return 0;
}

做出随机数生成器这道比较灵活的NOI的题目，就能真正开始接触矩阵乘法这一类的题目了
（NOI的T1对吧……裸的一匹……）

---

例题4：【NOIP2013模拟联考14】图形变换(transform)

problem

Description

翔翔最近接到一个任务，要把一个图形做大量的变换操作，翔翔实在是操作得手软，决定写个程序来执行变换操作。

翔翔目前接到的任务是，对一个由n个点组成的图形连续作平移、缩放、旋转变换。相关操作定义如下：

Trans(dx,dy) 表示平移图形，即把图形上所有的点的横纵坐标分别加上dx和dy；

Scale(sx,sy) 表示缩放图形，即把图形上所有点的横纵坐标分别乘以sx和sy；

Rotate(θ,x0,y0) 表示旋转图形，即把图形上所有点的坐标绕(x0,y0)顺时针旋转θ角度

由于某些操作会重复运行多次，翔翔还定义了循环指令：

Loop(m)

…

End

表示把Loop和对应End之间的操作循环执行m次，循环可以嵌套。

Input

第一行一个整数n(n<=100)表示图形由n个点组成；

接下来n行，每行空格隔开两个实数xi，yi表示点的坐标；

接下来一直到文件结束，每行一条操作指令。保证指令格式合法，无多余空格。

Output

输出有n行，每行两个空格隔开实数xi，yi表示对应输入的点变换后的坐标。

本题采用Special Judge判断，只要你输出的数值与标准答案误差不能超过1即可。

Sample Input

3

0.5 0

2.5 2

-4.5 1

Trans(1.5,-1)

Loop(2)

Trans(1,1)

Loop(2)

Rotate(90,0,0)

End

Scale(2,3)

End

Sample Output

10.0000 -3.0000

18.0000 15.0000

-10.0000 6.0000

Data Constraint

保证操作中坐标值不会超过double范围，输出不会超过int范围；

指令总共不超过1000行；

对于所有的数据,所有循环指令中m<=1000000；

对于60%的数据,所有循环指令中m<=1000；

对于30%的数据不含嵌套循环。

Hint

【友情提醒】

pi的值最好用系统的值。C++的定义为：#define Pi M_PI

Pascal就是直接为：pi

不要自己定义避免因为pi带来的误差。

---

analysis

30%的数据用模拟美滋滋地就能水分，但是——

指令总共不超过1000行；对于所有的数据,所有循环指令中m<=1000000

100%数据模拟GG

正解仍旧是矩阵乘法！
可以发现，对一个Loop—End循环操作 m m 次，相当于乘上某个和谐的矩阵 m m 次
所以就需要矩阵乘法来解决模拟太慢的问题了

---

构造矩阵式

首先这道 蜜汁 计算几何的题目需要一个旋转公式

顺点a,b逆时针旋转θ° 顺 点 a , b 逆 时 针 旋 转 θ °

x′=(x−a)×cosθ−(y−b)×sinθ+a x ′ = ( x − a ) × c o s θ − ( y − b ) × s i n θ + a

y′=(x−a)×sinθ−(y−b)×cosθ+b y ′ = ( x − a ) × s i n θ − ( y − b ) × c o s θ + b

如何构造矩阵？

设 A=(x,y,1) A = ( x , y , 1 ) （添加无用常数项），分别构造 T1,T2,T3 T 1 , T 2 , T 3 使：

A×T1=(x+a,y+b,1) A × T 1 = ( x + a , y + b , 1 )

A×T2=(ax,by,1) A × T 2 = ( a x , b y , 1 )

A×T3=((x−a)×cosθ−(y−b)×sinθ+a,(x−a)×sinθ−(y−b)×cosθ+b,1) A × T 3 = ( ( x − a ) × c o s θ − ( y − b ) × s i n θ + a , ( x − a ) × s i n θ − ( y − b ) × c o s θ + b , 1 )

我们经过一番和谐拆项以后，得到这三个东东：

T1=⎛⎝⎜1,0,00,1,0a,b,1⎞⎠⎟ T 1 = ( 1 , 0 , 0 0 , 1 , 0 a , b , 1 )

T2=⎛⎝⎜a,0,00,b,00,0,1⎞⎠⎟ T 2 = ( a , 0 , 0 0 , b , 0 0 , 0 , 1 )

T3=⎛⎝⎜cosθ,sinθ,0−sinθ,cosθ,0a−a×cosθ+b×sinθ,b−a×sinθ−b×cosθ,1⎞⎠⎟ T 3 = ( c o s θ , s i n θ , 0 − s i n θ , c o s θ , 0 a − a × c o s θ + b × s i n θ , b − a × s i n θ − b × c o s θ , 1 )

得到三个转移矩阵，套上一个栈模拟或dfs，就可以了
初始时 A=⎛⎝⎜1,0,00,1,00,0,1⎞⎠⎟ A = ( 1 , 0 , 0 0 , 1 , 0 0 , 0 , 1 ) （零矩阵）每退出一个Loop—End循环，就分三类情况累乘 A A 矩阵
最后把每个点都乘上 A A 矩阵，输出，AC

---

code

这题好像没怎么卡精度，好评

#include
#define Pi 3.14159265358979323846264338327950

using namespace std;

struct matrix
{
    double m[3][3];
};

matrix door[101];
char st[101];
int n;

matrix I=
{
    1,0,0,
    0,1,0,
    0,0,1
};

matrix operator *(matrix a,matrix b)
{
    matrix c;
    for (int i=0;i<=2;i++)
    {
        for (int j=0;j<=2;j++)
        {
            c.m[i][j]=0;
            for (int k=0;k<=2;k++)c.m[i][j]+=a.m[i][k]*b.m[k][j];
        }
    }
    return c;
}

matrix power(matrix a,int k)
{
    matrix ans=I,p=a;
    while (k)
    {
        if (k&1)ans=ans*p;
        p=p*p;
        k/=2;
    }
    return ans;
}

matrix dfs(int t)
{
    matrix a,tmp1,tmp2,tmp3;
    a=tmp1=
    {
        1,0,0,
        0,1,0,
        0,0,1
    };
    tmp2.m[2][2]=1;
    tmp3.m[2][2]=1;
    int now;
    for (scanf("%s",st);*st!='E';scanf("%s",st))
    {
        double theta,x,y;
        switch (*st)
        {
            case 'T':
            {
                sscanf(st,"Trans(%lf,%lf",&tmp1.m[2][0],&tmp1.m[2][1]);
                a=a*tmp1;
            }
            break;
            case 'S':
            {
                sscanf(st,"Scale(%lf,%lf",&tmp2.m[0][0],&tmp2.m[1][1]);
                a=a*tmp2;
            }
            break;
            case 'R':
            {
                sscanf(st,"Rotate(%lf,%lf,%lf",&theta,&x,&y);
                double _sin=sin(-theta/180*Pi),_cos=cos(-theta/180*Pi);
                tmp3=
                {
                    _cos,_sin,0,
                    -_sin,_cos,0,
                    x-x*_cos+y*_sin,y-x*_sin-y*_cos,1
                };
                a=a*tmp3;
            }
            break;
            default:
            {
                sscanf(st,"Loop(%d",&now);
                a=a*dfs(now);
            }
        }
    }
    return power(a,t);
}

int main()
{
    freopen("transform.in","r",stdin);
    freopen("transform.out","w",stdout);
    //freopen("readin.txt","r",stdin);
    scanf("%d",&n);
    for (int i=1;i<=n;i++)
    {
        scanf("%lf%lf",&door[i].m[0][0],&door[i].m[0][1]);
        door[i].m[0][2]=1;
    }
    matrix a,tmp1,tmp2,tmp3;
    a=tmp1=
    {
        1,0,0,
        0,1,0,
        0,0,1
    };
    tmp2.m[2][2]=1;
    tmp3.m[2][2]=1;
    while (scanf("%s",st)==1)
    {
        double theta,x,y;
        switch (*st)
        {
            case 'T':
            {
                sscanf(st,"Trans(%lf,%lf",&tmp1.m[2][0],&tmp1.m[2][1]);
                a=a*tmp1;
            }
            break;
            case 'S':
            {
                sscanf(st,"Scale(%lf,%lf",&tmp2.m[0][0],&tmp2.m[1][1]);
                a=a*tmp2;
            }
            break;
            case 'R':
            {
                sscanf(st,"Rotate(%lf,%lf,%lf",&theta,&x,&y);
                double _sin=sin(-theta/180*Pi),_cos=cos(-theta/180*Pi);
                tmp3=
                {
                    _cos,_sin,0,
                    -_sin,_cos,0,
                    x-x*_cos+y*_sin,y-x*_sin-y*_cos,1
                };
                a=a*tmp3;
            }   
            break;
            default:
            {
                int x;
                sscanf(st,"Loop(%d",&x);
                a=a*dfs(x);
            }
        }
    }
    for (int i=1;i<=n;i++)
    {
        printf("%.4lf %.4lf\n",(door[i]*a).m[0][0],(door[i]*a).m[0][1]);
    }
    return 0;
}

这题对没学过的人来说算是比较日脑子了，计算几何+矩阵乘法差评

---

后话

看到这里，觉得对矩阵乘法有一点理解了吗？
上面这些大概就是矩阵乘法的入门了，OI里用到矩阵乘法的地方较多
（犇：欸矩乘不是优化DP方程的么……）
恩，如果以后还有好的矩阵乘法例题，我会再贴到这里的

---

章节检索