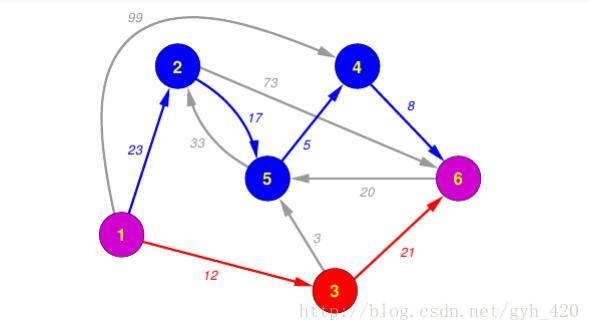
最小费用最大流问题

基于网络最大流问题，进一步提出的最小费用问题，费用权值和最大流问题的容量限制是两个概念，实质上这个问题就是求图的加权最短路，只是要在最大流的前提下实现。所以要用Bellman-Ford算法找增广路的同时计算最小费。
下面是紫书中求最小费最大流的模板`

const int maxn = 2000 + 10;
const int INF = 1000000000;

struct Edge {
  int from, to, cap, flow, cost;
  Edge(int u, int v, int c, int f, int w):from(u),to(v),cap(c),flow(f),cost(w) {}
};

struct MCMF {
  int n, m;
  vector edges;
  vector<int> G[maxn];
  int inq[maxn];         // 是否在队列中
  int d[maxn];           // Bellman-Ford
  int p[maxn];           // 上一条弧
  int a[maxn];           // 可改进量

  void init(int n) {
    this->n = n;
    for(int i = 0; i < n; i++) G[i].clear();
    edges.clear();
  }

  void AddEdge(int from, int to, int cap, int cost) {
    edges.push_back(Edge(from, to, cap, 0, cost));
    edges.push_back(Edge(to, from, 0, 0, -cost));
    m = edges.size();
    G[from].push_back(m-2);
    G[to].push_back(m-1);
  }

  bool BellmanFord(int s, int t, int flow_limit, int& flow, int& cost) {
    for(int i = 0; i < n; i++) d[i] = INF;
    memset(inq, 0, sizeof(inq));
    d[s] = 0; inq[s] = 1; p[s] = 0; a[s] = INF;

    queue<int> Q;
    Q.push(s);
    while(!Q.empty()) {
      int u = Q.front(); Q.pop();
      inq[u] = 0;
      for(int i = 0; i < G[u].size(); i++) {
        Edge& e = edges[G[u][i]];
        if(e.cap > e.flow && d[e.to] > d[u] + e.cost) {
          d[e.to] = d[u] + e.cost;
          p[e.to] = G[u][i];
          a[e.to] = min(a[u], e.cap - e.flow);
          if(!inq[e.to]) { Q.push(e.to); inq[e.to] = 1; }
        }
      }
    }
    if(d[t] == INF) return false;
    flow += a[t];
    cost += d[t] * a[t];
    for(int u = t; u != s; u = edges[p[u]].from) {
      edges[p[u]].flow += a[t];
      edges[p[u]^1].flow -= a[t];
    }
    return true;
  }

  // 需要保证初始网络中没有负权圈
  int MincostFlow(int s, int t, int flow_limit, int& cost) {
    int flow = 0; cost = 0;
    while(flow < flow_limit && BellmanFord(s, t, flow_limit, flow, cost));
    return flow;
  }

};

还有一道题目
Admiral UVA - 1658

使用的是拆点法：把2~v-1的每个点都拆成i和i’两个，然后i和i’间连一个容量1，费用为0的边，最后限制最大流为2时的最小费用即可。

拆解的办法：对点2~n-1拆成弧i->i’，前者（节点）编号为1~n-2，后者编号为n~2n-3
for(int i = 2; i <= n-1; i++)
T.AddEdge(i-1, i+n-2, 1, 0);
对于 flow += a[t]的a[t]要做个限幅，最大流量不能超过2要保证计算出的最小费用是在流量为2的前提下
while(flow < flow_limit && BellmanFord(s, t, flow_limit, flow, cost));
完整代码如下：

// UVA1658.cpp : 定义控制台应用程序的入口点。
//
#include 
#include 
#include 
#include 
using namespace std;
#define INF 1000000000
const int maxn = 2005;
struct Edge{
    int from, to, cap, flow, cost;//起点，终点，容量，流量，花费
    Edge(int u, int v, int c, int f, int w) :from(u), to(v), cap(c), flow(f), cost(w)
    {
    }//构造函数
};
struct mincmaxf{
    int n, m;//n表示结点数目，m表示边的数目
    vectoredges;
    vector<int>G[maxn];
    int inq[maxn];//标记是否在队列中
    int d[maxn];//费用记录，即是bellman-ford算法中的最短路
    int p[maxn];//指向父边，上一条边,为了找完一条通路后进行增广
    int delta[maxn];//记录残留网络值

    void init(int n){
        this->n = n;
        for (int i = 0; i < n; i++)
            G[i].clear();
        edges.clear();
    }
    void AddEdge(int from, int to, int cap,int cost){
        edges.push_back(Edge(from, to, cap, 0, cost));
        edges.push_back(Edge(to, from, 0, 0, -cost));
        m = edges.size();
        G[from].push_back(m - 2);
        G[to].push_back(m - 1);
    }
    bool BellmanFord(int s, int t, int flow_limit, int &flow, long long &cost)
    {
        for (int i = 0; i < n; i++)
            d[i] = INF;
        memset(inq, 0, sizeof(inq));
        d[s] = 0; inq[s] = 1; p[s] = 0; delta[s] = INF;

        queue<int>Q;
        Q.push(s);
        while (!Q.empty()){
            int u = Q.front(); Q.pop();
            inq[u] = 0;//代表u出队了
            for (int i = 0; iif (e.cap>e.flow&&d[e.to] > d[e.from] + e.cost)
                {
                    d[e.to] = d[u] + e.cost;//更新最小花费
                    p[e.to] = G[u][i];
                    delta[e.to] = min(delta[u], e.cap - e.flow);//更新残留网络值
                    if (!inq[e.to]){//防止回溯搜索时再次搜到已经搜索过的边
                        Q.push(e.to);
                        inq[e.to] = 1;
                    }
                }
            }
        }
        if (d[t] == INF)return false;

        //这句在本题中可要可不要，要了更严谨一些
        //if (flow + delta[t] > flow_limit) delta[t] = flow_limit - flow;

        flow += delta[t];
        cost += (long long)d[t] * (long long) delta[t];//求出当前费用
        for (int u = t; u != s; u = edges[p[u]].from)//回溯
        {
            edges[p[u]].flow += delta[t];
            edges[p[u]^1].flow -= delta[t];
        }
        return true;
    }
    int MincostMaxFlow(int s, int t, int flow_limit,long long &cost)
    {
        int flow = 0;
        cost = 0;
        while (BellmanFord(s, t, flow_limit, flow, cost)&&flow return flow;
    }
};

int main()
{
    int n=0, m = 0;
    mincmaxf T;
    int div[1005];
    while (cin >> n >> m &&n>0)
    {
        int a1, a2, a3;
        int temp = n;
        long long mincost;
        memset(div, 0, sizeof(div));
        T.init(n*2-2);
        for (int i = 2; i <= n - 1; i++)
            T.AddEdge(i - 1, i + n - 2, 1, 0);

        for (int i = 0; i < m; i++)
        {   
            cin >> a1>>a2 >> a3;        
            if (a1 != 1 && a1 != n) a1 += n - 2; 
            else a1--;
            a2--;
            T.AddEdge(a1, a2, 1, a3);
        }
        T.MincostMaxFlow(0, n-1, 2,mincost);
        cout << mincost << endl;
    }
    return 0;
}